Sum of squares

给定一个线性回归模型 yi = β0 + β1xi1 +…+ βpxi1 + εi  

对应数据集(xi1, xi2,…, xip, yi), i=1,…,n，包含n个观察数据. β是系数，ε 是误差项

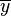\overline{y}表示y的期望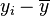， y_i - \overline{y}就是离差(deviation)，注意不是方差(variance);  \hat{y_i} 表示对yi预测的值.

The total sum of squares(TSS) = the explained sum of squares(ESS) + the residual sum of squares(RSS),对应于：

在普通最小二乘法(Ordinary Least Squares)中的应用

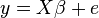
　　 y = X \beta + e

对β的估计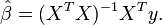： \hat \beta = (X^T X)^{-1}X^T y.

The residual vector 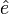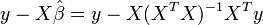\hat e = y - X \hat \beta = y - X (X^T X)^{-1}X^T y，则

　　

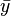用 \bar y 表示向量，其每个元素都相等，为 y 的期望，则

　　

让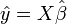 \hat y = X \hat \beta，则

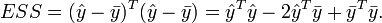
　　 ESS = (\hat y - \bar y)^T(\hat y - \bar y) = \hat y^T \hat y - 2\hat y^T \bar y + \bar y ^T \bar y.

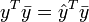当且仅当 y^T \bar y = \hat y^T \bar y(也即the sum of the residuals )时，TSS = ESS + RSS.

（由于，,

或 \hat \varepsilon ^T X = \left( {\mathbf{y}} - {\mathbf{\hat y}} \right)^T X = {\mathbf{y}}^T\left( {I - X\left( {X^T X} \right)^{ - 1} X^T } \right)X = {\mathbf{y}}^T\left(X-X \right)={\mathbf{0}}.

而X的第一列全是1，则X^T \hat e第一个元素就是，并且等于0. 

因此上面的条件成立，可使TSS = ESS + RSS）

Mean squared error(MSE)

posted on 2012-12-11 19:59  liangzh123  阅读(1335)  评论(0)    收藏  举报

导航