教学目标:
1. 了解动力学普遍方程。
2. 能正确地运用拉格朗日方程建立质点系的运动微分方程。
本章重点、难点:
选广义坐标,并将质点动能表示为广义坐标和广义速度的函数。
计算广义力或将保守系统的势函数表示为广义坐标的函数。
教学过程:
引言:本章是把达朗伯原理和虚位移原理结合起来,推导出
求解质点系动力学问题的最普通的方程,是分析动力学的基
础。
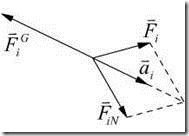
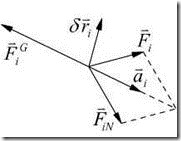
一.动力学普遍方程
由达朗伯原理,有
由虚位移原理,有:
将以上几个方程相加,有:
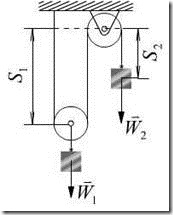
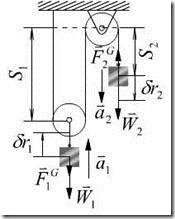
例16.1 已知:在图16.2所示滑轮系统中,动滑轮上悬挂重为![]() 的重物,绳子绕过定滑轮后悬挂重为
的重物,绳子绕过定滑轮后悬挂重为![]() 的重物,设滑轮和绳子的重量不计,求:重为
的重物,设滑轮和绳子的重量不计,求:重为![]() 的重物的加速度
的重物的加速度
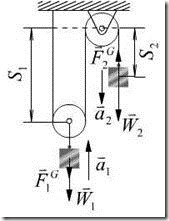
3,分析运动,虚加惯性力,
如图16.2所示,其中
5,由动力学普遍方程求解:
将惯性力和虚位移关系代入上式,
二.拉格朗日方程
1, 方程推导,
将动力学普遍方程变换为
代入式(a)
两个经典关系式:
式(1)的证明:
式(2)的证明:
将式(1),(2)代入式(c),有:
完整系统中,![]() 是彼此独立的,可得:
是彼此独立的,可得:![]() -------------- 拉格朗日第二类方程
-------------- 拉格朗日第二类方程
方程的性质,关于![]() 的二阶微分方程组,可求解运动及主动力,不能求约束力。
的二阶微分方程组,可求解运动及主动力,不能求约束力。
2, 保守系统的拉氏方程
3, 拉格朗日方程的应用
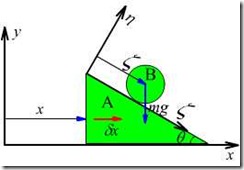
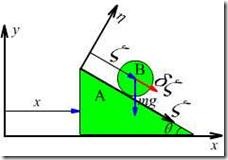
例16.2,已知:三棱柱![]() 质量为
质量为![]() ,与水平面光滑接触,均质圆柱质量为
,与水平面光滑接触,均质圆柱质量为![]() ,半经为
,半经为![]() ,放在三棱柱的斜面上,圆柱与三棱柱之间无相对滑动,不计滚动摩阻,设
,放在三棱柱的斜面上,圆柱与三棱柱之间无相对滑动,不计滚动摩阻,设![]() (图16.3)
(图16.3)
2,分析主动力,计算广义力:
4, 计算偏导数,代入拉氏方程
5, 求解
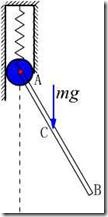
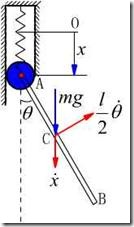
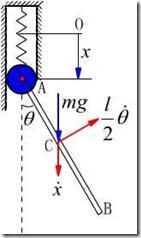
例16.3,已知:质量为![]() 长度为
长度为![]() 的均质杆
的均质杆![]() ,
,![]() 端与钢性系数为
端与钢性系数为![]() 的弹簧相连并限制在铅垂方向运动,
的弹簧相连并限制在铅垂方向运动,![]() 杆还可以绕过
杆还可以绕过![]() 的水平轴摆动,如图16.4所示,求:
的水平轴摆动,如图16.4所示,求:![]() 杆的运动微分方程,
杆的运动微分方程,
2,分析运动,计算动能
3,分析主动力,计算势能,并写出拉氏函数
设平衡时![]() 点的位置为坐标原点
点的位置为坐标原点![]() ,并设平衡位置为弹力和重力的零势能点,有:
,并设平衡位置为弹力和重力的零势能点,有:
4,计算偏导数,代入拉氏方程




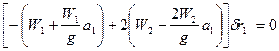
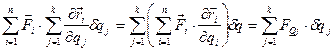
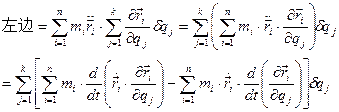
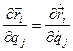
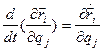
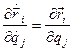
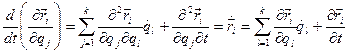
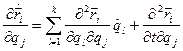
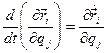
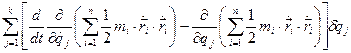
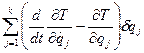
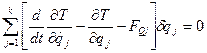
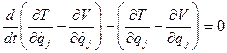
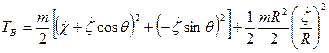


 浙公网安备 33010602011771号
浙公网安备 33010602011771号