【十大算法实现之naive bayes】朴素贝叶斯算法之文本分类算法的理解与实现

关于bayes的基础知识，请参考：

　　基于朴素贝叶斯分类器的文本聚类算法 （上） http://www.cnblogs.com/phinecos/archive/2008/10/21/1315948.html 
　　基于朴素贝叶斯分类器的文本聚类算法 （下） http://www.cnblogs.com/phinecos/archive/2008/10/21/1316044.html

　　算法杂货铺——分类算法之朴素贝叶斯分类　　http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

　　网上的数据源： http://archive.ics.uci.edu/ml/

　　斯坦福大学公开课 ：机器学习课程:朴素贝叶斯算法 http://v.163.com/movie/2008/1/7/H/M6SGF6VB4_M6SGJVV7H.html

 

P(Y|X)称为Y的后验概率（posterior probability），与之相对的，P(Y)称为Y的先验概率（prior probability）

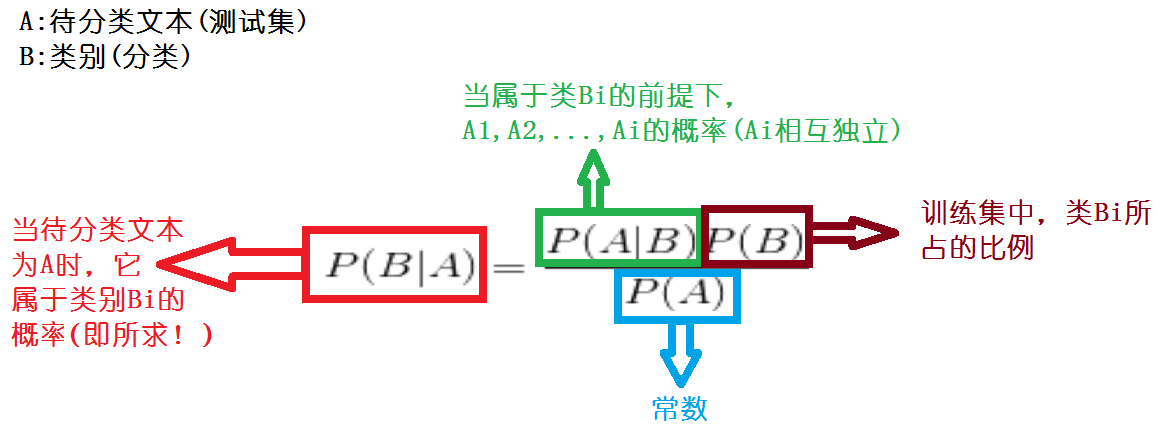
测试集：　 
7月12日电 据外电报道，在离开克里夫兰骑士，前往迈阿密热火为追逐冠军4年之后，小皇帝詹姆斯宣布回家了！詹姆斯在《体育画报》网站上以第一人称发表了一份声明，小皇帝决定带着妻儿回家直到退役。 
　 “我一直都相信我会回到克里夫兰，并在那里结束自己的职业生涯，”詹姆斯说道，“只是我不知道什么时候会回去。在赛季结束后，我并没有考虑过自由选择权。但我现在已经有两个儿子，我妻子又怀上了一个女孩，我开始想，如果能带着整个家庭回到家乡生活会是怎样。我也看到了其他的球队，但我从未想过离开迈阿密会去克里夫兰以外的地方。时间过得越久，我越觉得这个想法是正确的。这个决定让我很开心。” 
在连续四年闯入NBA总决赛并拿到两座总冠军之后，詹姆斯要与韦德和波什分别了。据悉，波什也在筹划离开热火。消息源称，就在詹姆斯宣布回归骑士后，火箭开始筹划交易林书豪，来为波什4年8800万美元的合同腾出薪金空间。 

 

简述处理过程： 

1、构造bayes分类器（引用jar包）； 

 

2、中文分词处理ChineseSpliter.split()： 
7月, 12日, 电, 据外电报道, 离开, 克里夫兰, 骑士, 前往, 迈阿密, 热火, 追逐, 冠军, 4年, 之后, 小皇帝, 詹姆斯, 宣布, 回家, 詹姆斯, 体育, 画报, 网站, 第一人称, 发表, 一份, 声明, 小皇帝, 决定, 带着, 妻儿, 回家, 直到, 退役, 我, 一直都, 相信, 我会, 回到, 克里夫兰, 并在, 那里, 结束, 自己, 职业, 生涯, 詹姆斯, 说道, 只是, 我不, 知道, 什么时候, 会, 回去, 赛季, 结束, 我并, 没有, 考虑, 过, 自由选择, 权, 但我, 现在, 已经有, 两个, 儿子, 我, 妻子, 怀, 上了, 一个, 女孩, 我, 开始, 想, 如果能, 带着, 整个, 家庭, 回到, 家乡, 生活会, 怎样, 我也, 看到了, 其他, 球队, 但我, 从未, 想过, 离开, 迈阿密, 会去, 克里夫兰, 以外, 地方, 时间, 过得, 越久, 我, 越, 觉得, 这个, 想法, 正确, 这个, 决定, 让我, 开心, 连续, 四年, 闯入, nba, 总决赛, 拿到, 两座, 总, 冠军, 之后, 詹姆斯, 要, 韦德, 波什, 分别, 据悉, 波什, 也在, 筹划, 离开, 热火, 消息, 源, 称, 就在, 詹姆斯, 宣布, 回归, 骑士, 火箭, 开始, 筹划, 交易, 林书豪, 波什, 4年, 8800万, 美元, 合同, 腾出, 薪金, 空间 


3、删除常用停用词： 
stopWordsList[] ={"的", "我","我们","要","自己","之","将","“","”","，","（","）","后","应","到","某","后","个","是","位","新","一","两","在","中","或","有","更","好",""}; 

7月, 12日, 电, 据外电报道, 离开, 克里夫兰, 骑士, 前往, 迈阿密, 热火, 追逐, 冠军, 4年, 之后, 小皇帝, 詹姆斯, 宣布, 回家, 詹姆斯, 体育, 画报, 网站, 第一人称, 发表, 一份, 声明, 小皇帝, 决定, 带着, 妻儿, 回家, 直到, 退役, 一直都, 相信, 我会, 回到, 克里夫兰, 并在, 那里, 结束, 职业, 生涯, 詹姆斯, 说道, 只是, 我不, 知道, 什么时候, 会, 回去, 赛季, 结束, 我并, 没有, 考虑, 过, 自由选择, 权, 但我, 现在, 已经有, 两个, 儿子, 妻子, 怀, 上了, 一个, 女孩, 开始, 想, 如果能, 带着, 整个, 家庭, 回到, 家乡, 生活会, 怎样, 我也, 看到了, 其他, 球队, 但我, 从未, 想过, 离开, 迈阿密, 会去, 克里夫兰, 以外, 地方, 时间, 过得, 越久, 越, 觉得, 这个, 想法, 正确, 这个, 决定, 让我, 开心, 连续, 四年, 闯入, nba, 总决赛, 拿到, 两座, 总, 冠军, 之后, 詹姆斯, 韦德, 波什, 分别, 据悉, 波什, 也在, 筹划, 离开, 热火, 消息, 源, 称, 就在, 詹姆斯, 宣布, 回归, 骑士, 火箭, 开始, 筹划, 交易, 林书豪, 波什, 4年, 8800万, 美元, 合同, 腾出, 薪金, 空间

 

4、步骤3执行完毕算式得到了真正的测试样本x，根据给定的文本属性向量在给定的分类中计算分类条件概率，先取第一个分类——IT 
根据公式P（x|C=”IT”）= P（x=”7月”|C=”IT”） * P（x=”12月”|C=”IT”）* P（x=”电”|C=”IT”） * P（x=”据外电报道”|C=”IT”） * ……*P（x=”空间”|C=”IT”）==>得到ans（因为文本属性向量相互独立） 

 1  /**
 2     * 计算给定的文本属性向量X在给定的分类Cj中的类条件概率
 3     * <code>ClassConditionalProbability</code>连乘值
 4     * @param X 给定的文本属性向量
 5     * @param Cj 给定的类别
 6     * @return 分类条件概率连乘值，即<br>
 7     */
 8     float calcProd(String[] X, String Cj) 
 9     {
10         float ret = 1.0F;
11         // 类条件概率连乘
12         for (int i = 0; i <X.length; i++)                   //步骤4
13         {
14             String Xi = X[i];
15             //因为结果过小，因此在连乘之前放大10倍，这对最终结果并无影响，因为我们只是比较概率大小而已
16             ret *=ClassConditionalProbability.calculatePxc(Xi, Cj)*zoomFactor;
17         }
18         // 再乘以先验概率
19         ret *= PriorProbability.calculatePc(Cj);                   //步骤5
20         return ret;
21     }
P（x=”？”|C=”IT”）的计算=（给定分类中包含关键字／词的训练文本的数目）/（训练文本集中在给定分类下的训练文本数目+训练文本类别） 

5、根据bayes公式，P（C=”IT”）P（x|C=”IT”）= P（C=”IT”）* ans=P（（x）∩（C=”IT”）） 
P（C=”？”）的计算=（训练文本集中在给定分类下的训练文本数目）/（训练文本集中所有的文本数目） 

6、重复4、5，计算出P（（x）∩（C=”汽车”））、P（（x）∩（C=”健康”））、P（（x）∩（C=”军事”））……最后取最大值，也就是最有可能的。
 
1、2、3属于准备阶段 
4、5、6包含了分类器的训练阶段以及利用已训练好的分类器的应用阶段 
P（C=”？”）的计算就是分类器的训练过程，即计算先验概率 
 
 1 /**
 2 * 先验概率计算
 3 * P(cj)=N(C=cj)/N
 4 * 其中，N(C=cj)表示类别cj中的训练文本数量；
 5 * N表示训练文本集总数量。
 6 */
 7 
 8 public class PriorProbability 
 9 {
10     private static TrainingDataManager tdm =new TrainingDataManager();
11     /**
12     * 先验概率
13     * @param c 给定的分类
14     * @return 给定条件下的先验概率
15     */
16     public static float calculatePc(String c)
17     {
18         float ret = 0F;
19         float Nc = tdm.getTrainingFileCountOfClassification(c);     //训练文本集中在给定分类下的训练文本数目
20         float N = tdm.getTrainingFileCount();                            //训练文本集中所有的文本数目
21         ret = Nc / N;
22         return ret;
23     }
24 }

训练样本为：TrainningSet文件夹，其中包含了各个类别的文本集。 

 


In process. 
IT：4.5137176E-26 
In process. 
体育：4.5942127E-8 
In process. 
健康：8.096193E-22 
In process. 
军事：2.7799264E-25 
In process. 
招聘：1.828473E-23 
In process. 
教育：6.3704085E-12 
In process. 
文化：1.114498E-25 
In process. 
旅游：2.8563375E-24 
In process. 
汽车：2.0799206E-14 
In process. 
财经：4.2796716E-22 
此项属于[体育] 

 

 

 

运行文件下载：

链接: http://pan.baidu.com/s/1hq88LA8 密码: 05w3

 

 

 

 后来，又用了naive bayes做了代码的分类，遇到了很多问题。

  • 训练集过大，运行时间过慢

　　　　平均800KB的文件中大约含有20000个单词

过程简述：
a)    已知test（待测试的文本），对其进行分词（因为里面有很多的特殊符号和空格，所以自己写了一个过滤的方法，星期六上午写完了之后，给学长看了，提到了过滤的方法的不足的地方就是：我不应该把里面的全部数字都删除，而是应该把单独的代表量度的数字给删除，有些单词中包含数字作为变量名的应该保留下来）；
b)    训练分类器
c)    对test做分词处理，并去掉停用词
d)    正式开始进行分类操作：
i.    选取第一个分类A
ii.    获取A类下所有文件的路径
iii.    获取A类下第一个文本，并将其内容全部转化为String
iv.    从test中的第一个单词开始判断，是否存在与A类的第一个文本中
For(从第一个分类开始到最后一个分类)        7类
    For(从当前分类的第一个文本开始到当前分类的最后一个文本)  平均24文本，每个文本15000个单词
　　｛
   　　 For(从test的第一个单词到test最后一个单词)    平均有15000个单词
　　　　｛
　　　　　　　　If(该单词在这个文本中)    
　　　　　　　　｛
　　　　　　　　　　　　Ret++;
　　　　　　　　　}
　　　　｝
　　　　P(test在当前分类的当前文本中的概率)
　　｝
　　P(test|分类Xi)
}
复杂度为：7*24*15000*15000=3.78*(10^10)

已经不能愉快的玩耍了

 

这里，以上naive bayes分类器代码存在的问题：

  • 需要尽可能保证每一个训练集大小基本一致：因为后验概率判断的是分词之后的单词是否存在与训练集某类的某个文本中，因此，文本较大的话，相对来说，
    • 可能含有单词的概率也大，这样，要是训练集A类中一个文本1kb，B类中一个文本1000kb，那么，显然是不合理的；
  • 程序耗时的问题，当处理较大训练集的时候，就会很慢
  • 之前的中文分类需要用到中文分词组件，而英文分词只要根据空格和标点就可以了

 

 

解决方案：

　　预处理(等于是先打表)：

　　　　利用java中的hashmap<String,Double>计算了每一类下每个单词出现的次数，然后处理每一类的总次数（A类下B单词出现的次数/A类单词总数）

　　之后直接读取hashmap中的数值就好。

程序下载：链接: http://pan.baidu.com/s/1ntwTI4L 密码: d9qi

 

 

费舍尔方法与贝叶斯方法的区别：

  • 贝叶斯方法： P(Category|Document)=P(Document|Category)*P(Category)/P(Document)

其中，P(Document|Category i)=P(feature 1|Category i)*P(feature 2|Category i)*......*P(feature N|Category i)

　　   P(Category)：先验概率

　　   P(Document)：常量（实际计算时不考虑）

  • 费舍尔法方法：

  1. 属于某分类的概率clf = Pr(feature | category)

     

  2. 属于所有分类的概率freqsum = Pr(feature | category)之和

  3.  

    cprob = clf / (clf+nclf)

　　　　P(Category i|feature 1)

　　费舍尔方法的计算过程是将所有概率相乘起来，然后取自然对数，再将所得结果乘以-2。

　　费舍尔方法告诉我们，如果概率彼此独立且随机分布，则这一计算结果将满足对数卡方分布（chi-squared distribution）。也许我们会预料到，不属于某个分类的内容项中，可能会包含针对该分类的不同特征概率的单词（可能会随机出现）；或者，一个属于该分类的内容项中会包含许多概率值很高的特征。通过将费舍尔方法的计算结果传给倒置对数卡方函数，我们会得到一组随机概率中的最大值。

　　

 

 

 

posted @ 2014-07-13 09:02  max_xbw  阅读(9183)  评论(0)  编辑  收藏  举报