python实现•十大排序算法之计数排序(Counting Sort)
简介
计数排序(Counting Sort)不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。它的基本思想是:给定的输入序列中的每一个元素x,确定该序列中值小于等于x元素的个数,然后将x直接存放到最终的排序序列的正确位置上。
算法实现步骤
- 根据待排序集合中最大元素和最小元素的差值范围,申请额外空间;
- 遍历待排序集合,将每一个元素出现的次数记录到元素值对应的额外空间内;
- 对额外空间内数据进行计算,得出每一个元素的正确位置;
- 将待排序集合每一个元素移动到计算得出的正确位置上。
Python 代码实现
# counting_sort 代码实现
from typing import List
def counting_sort(arr:List[int]):
max=min=0
for i in arr:
if i < min:
min = i
if i > max:
max = i
count = [0] * (max - min +1)
for j in range(max-min+1):
count[j]=0
for index in arr:
count[index-min]+=1
index=0
for a in range(max-min+1):
for c in range(count[a]):
arr[index]=a+min
index+=1
# 测试数据
if __name__ == '__main__':
import random
random.seed(54)
arr = [random.randint(0,100) for _ in range(10)]
print("原始数据:", arr)
counting_sort(arr)
print("计数排序结果", arr)
# 输出结果
原始数据: [17, 56, 71, 38, 61, 62, 48, 28, 57, 42]
计数排序结果 [17, 28, 38, 42, 48, 56, 57, 61, 62, 71]
动画演示
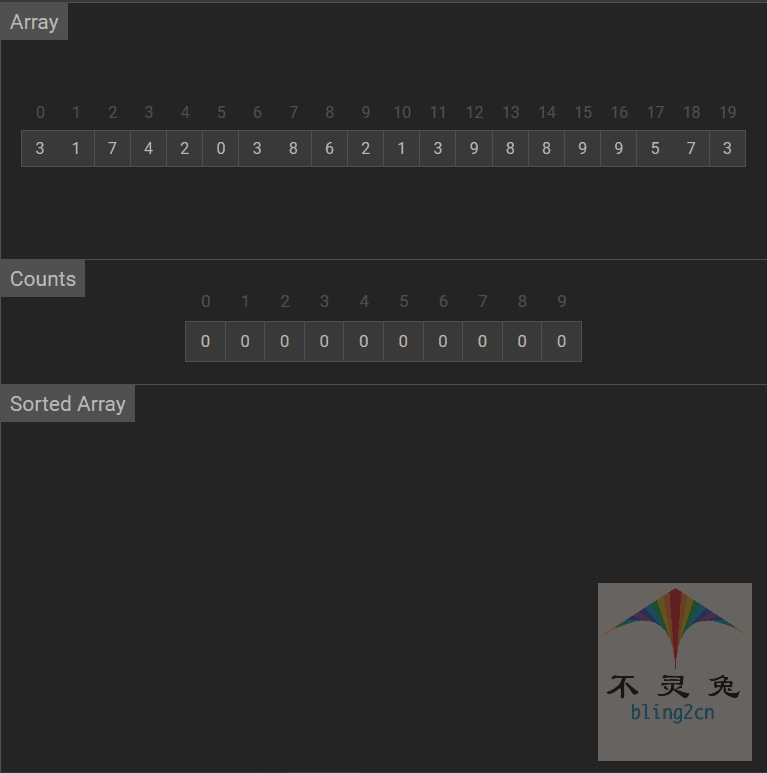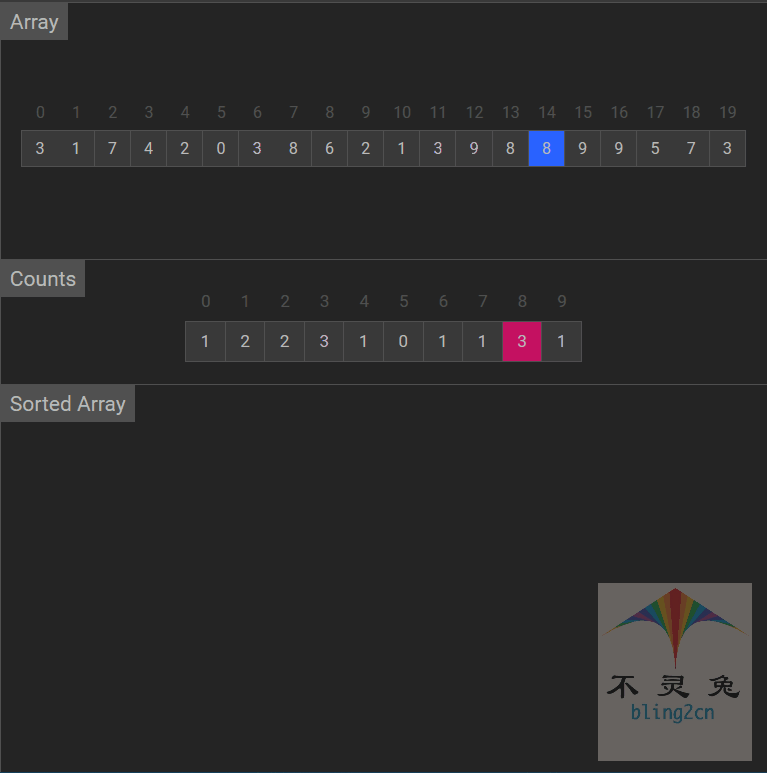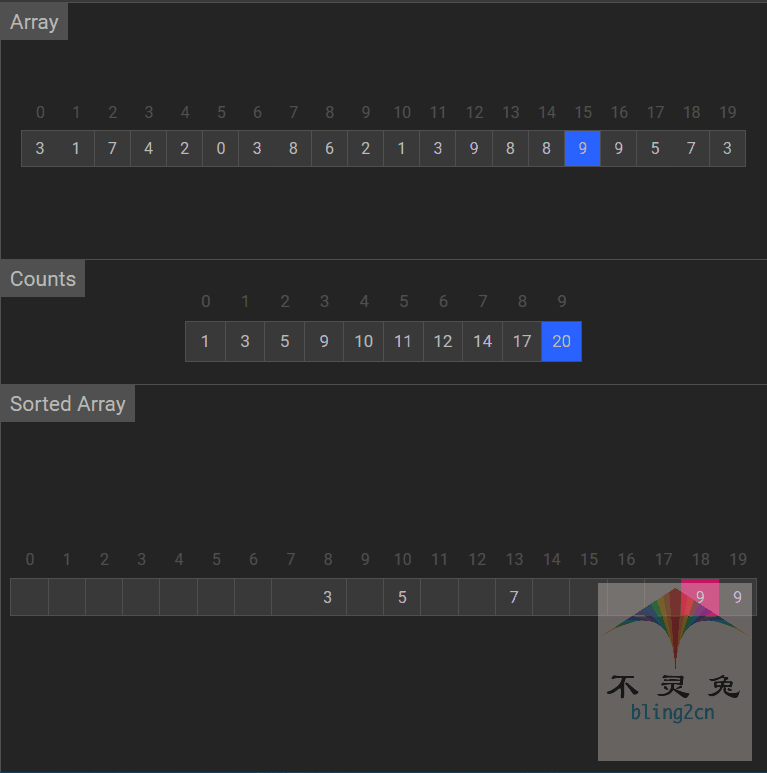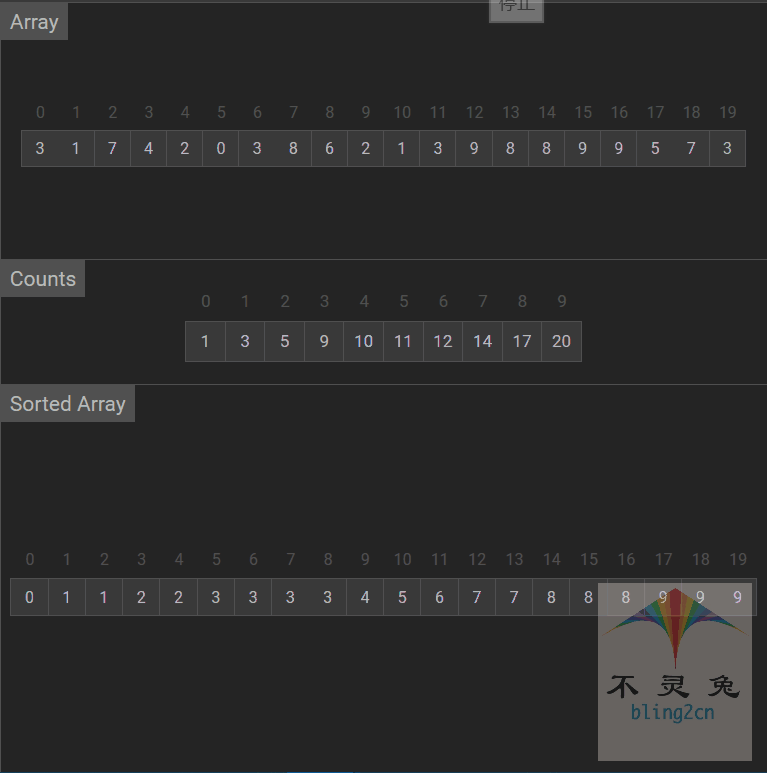
算法分析
-
时间复杂度
数据取值范围是常数 k,待排序元素个数是 n,总的时间复杂度是 \(O(n+ k)\)。
-
空间复杂度
计数排序只需要额外的空间复杂度为\(O(k)\),所以计数排序的空间复杂度为\(O(k)\)。
-
稳定性
计数排序不会改变相等元素的相对位置,所以计数排序是稳定的。
-
综合评价
时间复杂度(平均) 时间复杂度(最好) 时间复杂度(最坏) 空间复杂度 排序方式 稳定性 \(O(n+k)\) \(O(n+k)\) \(O(n+k)\) \(O(k)\) out-place 稳定
联系我们
个人博客网站:http://www.bling2.cn/
Github地址:https://github.com/lb971216008/Use-Python-to-Achieve
知乎专栏:https://zhuanlan.zhihu.com/Use-Python-to-Achieve
小专栏:https://xiaozhuanlan.com/Use-Python-to-Achieve
博客园:https://www.cnblogs.com/Use-Python-to-Achieve



 浙公网安备 33010602011771号
浙公网安备 33010602011771号