python实现•十大排序算法之快速排序(Quick Sort)
简介
快速排序(Quick Sort)是对冒泡排序的一种改进,其的基本思想:选一基准元素,依次将剩余元素中小于该基准元素的值放置其左侧,大于等于该基准元素的值放置其右侧;然后,取基准元素的前半部分和后半部分分别进行同样的处理;以此类推,直至各子序列剩余一个元素时,即排序完成(类比二叉树的思想)。
算法实现步骤
- 首先设定一个分界值(
pivot),通过该分界值将数组分成左右两部分。 - 将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值,这个称为分区(
partition)操作。 - 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
- 重复上述过程,通过递归(
recursive)将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
Python 代码实现
# quick_sort 代码实现
def partition(arr: List[int], low: int, high: int):
pivot, j = arr[low], low
for i in range(low + 1, high + 1):
if arr[i] <= pivot:
j += 1
arr[j], arr[i] = arr[i], arr[j]
arr[low], arr[j] = arr[j], arr[low]
return j
def quick_sort_between(arr: List[int], low: int, high: int):
if high-low <= 1: # 递归结束条件
return
m = partition(arr, low, high) # arr[m] 作为划分标准
quick_sort_between(arr, low, m - 1)
quick_sort_between(arr, m + 1, high)
def quick_sort(arr:List[int]):
"""
快速排序(in-place)
:param arr: 待排序的List
:return: 快速排序是就地排序(in-place)
"""
quick_sort_between(arr,0, len(arr) - 1)
# 测试数据
if __name__ == '__main__':
import random
random.seed(54)
arr = [random.randint(0,100) for _ in range(10)]
print("原始数据:", arr)
quick_sort(arr)
print("快速排序结果:", arr)
# 输出结果
原始数据: [17, 56, 71, 38, 61, 62, 48, 28, 57, 42]
快速排序结果: [17, 28, 38, 42, 48, 56, 57, 61, 62, 71]
动画演示
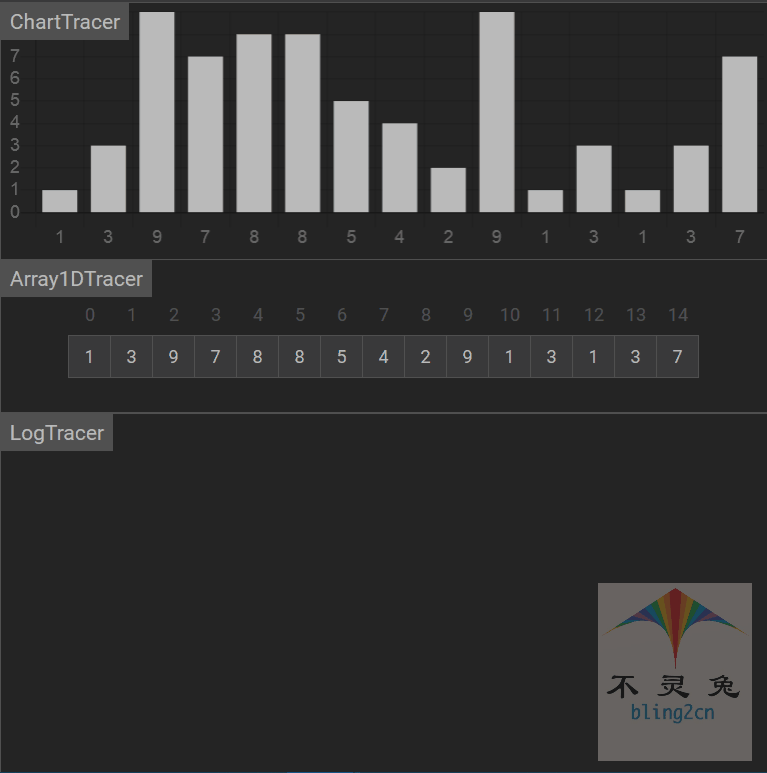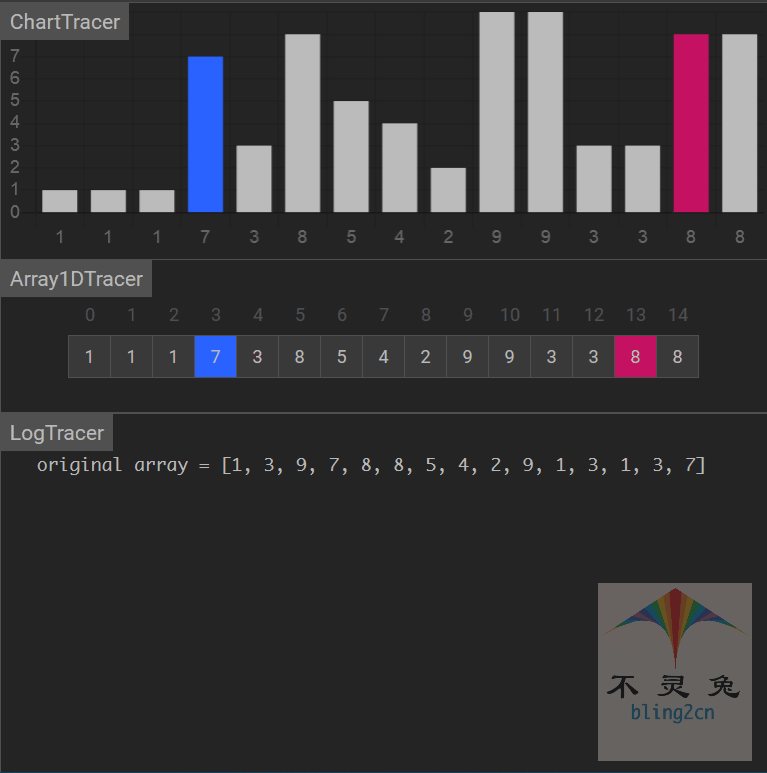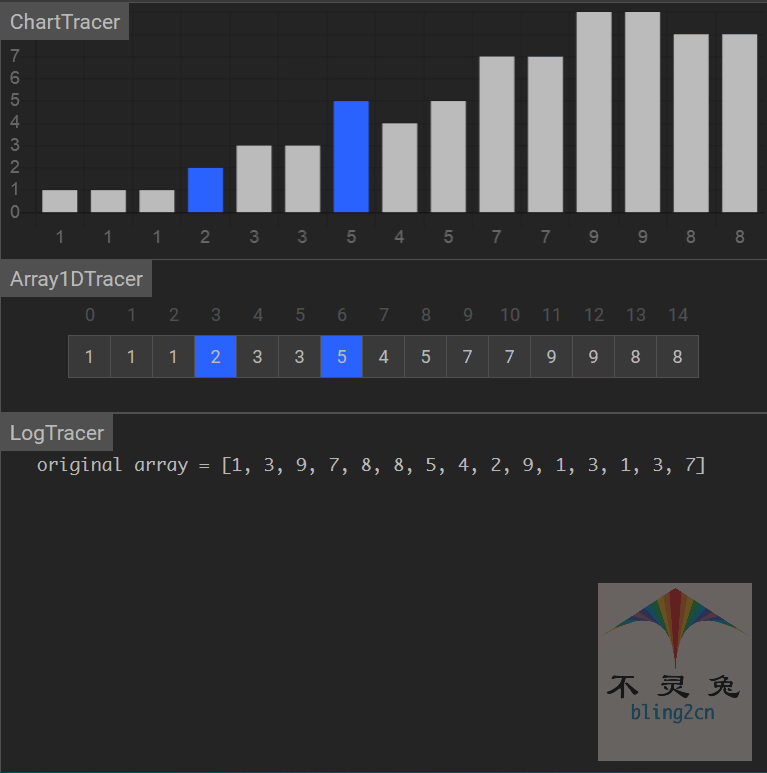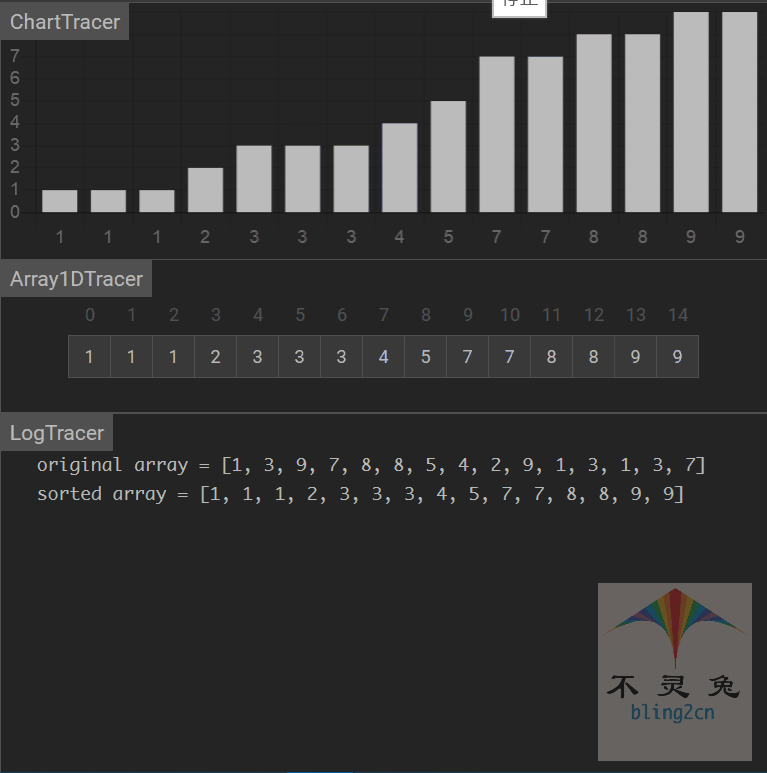
算法分析
-
时间复杂度
快速排序最优的情况就是每一次取到的元素都刚好平分整个数组,此时的时间复杂度公式则为:
\[T\left[ n \right] =2T\left[ \dfrac{n}{2} \right] \ +\ f\left( n \right) \]\(T\left[ n \right]\)为平分后的子数组的时间复杂度,\(f\left( n \right)\)为平分这个数组时所花的时间;
则有:
\[\begin{align} T\left[ n \right] &=2T\left[ \dfrac{n}{2} \right] +n &\text{第1次递归}n=n\\ &=2^2T\left[ \dfrac{n}{2^2} \right] +2n &\text{第2次递归}n=\dfrac{n}{2}\\ & =2^3T\left[ \dfrac{n}{2^3} \right] +3n &\text{第3次递归}n=\dfrac{n}{2^2}\\ &\cdots \cdots \\ &=2^mT\left[ \dfrac{n}{2^m} \right] +mn &\text{第m次递归}n=\dfrac{n}{2^m} \end{align} \]当最后平分的不能再平分时有:
\[\begin{align} &T\left[ \dfrac{n}{2^m} \right] =T\left[ 1 \right] \\ \Rightarrow &\frac{n}{2^m}=1 \\ \Rightarrow &m=\log _2n \\ \Rightarrow &T\left[ n \right] =n+n\log _2n=O(nlog_2n) \end{align} \]快速排序最优的情况下时间复杂度为:\(O\left( n\log _2n \right)\)
最差的情况就是每一次取到的元素就是数组中最小/最大值,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序),这种情况时间复杂度就是冒泡排序的时间复杂度:
\[T\left[ n \right] =n\left( n-1 \right) =n^2+n=O\left( n^2 \right) \]快速排序最差的情况下时间复杂度为:\(O(n^2)\)
快速排序的平均时间复杂度也是:\(O\left( n\log _2n \right)\)
-
空间复杂度
首先就地快速排序使用的空间是\(O(1)\)的,也就是个常数级。真正消耗空间的就是递归调用了,因为每次递归就要保持一些数据。
最优的情况是每一次都平分数组,空间复杂度为:\(O(log_2n)\) ;
最差的情况是退化为冒泡排序,空间复杂度为:\(O(n)\); -
稳定性
排序过程中,相同的元素无法保证相对位置不变,因此快速排序属于不稳定排序。
-
综合分析
时间复杂度(平均) 时间复杂度(最好) 时间复杂度(最坏) 空间复杂度 排序方式 稳定性 \(O(nlog_2n)\) \(O(nlog_2n)\) \(O(n^2)\) \(O(log_2n)\) in-place 不稳定
联系我们
个人博客网站:http://www.bling2.cn/
Github地址:https://github.com/lb971216008/Use-Python-to-Achieve
知乎专栏:https://zhuanlan.zhihu.com/Use-Python-to-Achieve
小专栏:https://xiaozhuanlan.com/Use-Python-to-Achieve
博客园:https://www.cnblogs.com/Use-Python-to-Achieve



 浙公网安备 33010602011771号
浙公网安备 33010602011771号