Paper | Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

• Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
  • 1. PROBLEM
    • 1.1 Introduction
    • 1.2 Analysis
  • 2. SOLUTION
    • 2.1 Batch Normalization及其问题
    • 2.2 梯度修正及其问题
    • 2.3 Key Algorithm
      • 对向量中的每一个标量进行标准化
      • Batch Normalizing Transform
      • Mini-batch
    • 2.4 Inference
    • 2.5 实际应用方式
  • 3. EFFECT

1. PROBLEM

1.1 Introduction

在网络中，当上一层的参数发生变化时，下一层网络的输入的分布就会发生变化。

The distribution of each layer's inputs changes during training, as the parameters of the previous layers change.

特别是对于深度网络，每一层的改动，都会对后面的层产生重大影响。

Small changes to the network parameters amplify as the network becomes deeper.

这导致：

• 学习率不能太高（参数不能变化太剧烈），进而导致训练缓慢。

• 每一层的初始化都必须非常细致。

• 遇到饱和问题的非线性网络将会更难训练。

我们将这一现象称为 internal covariate shift 。
总结成一句话，就是随着训练进行，各节点由于连接关系，导致输入分布时刻协同变化的问题。

为什么用 mini-batch 而不是整体，为什么用 normalization ，就不说了。

1.2 Analysis

对于某一层而言，它的输入的分布在不断变化（由于上一层参数的变化）。
显然，要拟合这种时刻变化的分布，是困难的。

The change in the distributions of layers’ inputs presents a problem because the layers need to continuously adapt to the new distribution.

这种输入分布的变化，就被称作 covariate shift 。

此外，对于出现饱和问题的网络，标准化输入也能发挥作用。
比如对一个 sigmoid 函数的输入，当其绝对值过大时，梯度就会消失。
如果是深度网络，饱和问题还会被逐层放大。
标准化可以保证输入的绝对值在0附近，从而缓解这一问题。

2. SOLUTION

2.1 Batch Normalization及其问题

对每一层输入的 mini-batch ，我们都进行 normalization 。

说到这里，大家肯定会想到一个问题：如果我们强行将每一层的输入都 whiten ，学习到的东西会不会有问题？
答案是肯定的。

举个例子：网络某一层的输出满足： \(x = wu + b\) ，有一个偏置参数 \(b\) 。
但在输入下一层并标准化时，\(b\) 就会出现在均值里从而被减掉。
因此最终的 output 一定与 \(b\) 无关。因此 \(b\) 也和 loss 无关。
换句话说，无论 \(b\) 怎么变， loss 都巍然不动。
但偏置 \(b\) 更新（梯度下降）时，其增量正比于其关于 loss 的偏导：

\[b = b + \Delta b \\ \Delta b \propto -\frac{\partial loss}{\partial b} \]

如果无视标准化步骤，那么该偏导将是：

\[\frac{\partial loss}{\partial b} = \frac{\partial loss}{\partial \hat x} \frac{\partial \hat x}{\partial b} = \frac{\partial loss}{\partial \hat x} \]

既然 loss 不变，那么该偏导的值就不变。假设该值是负的，那么 \(b\) 就会无限制增大！！！

这就是问题：\(b\) 的更新是错误的！
如果我们还考虑了 scaling ，显然情况会更糟。

再比如，如果是 sigmoid 函数，原始输入明明在非线性区，标准化非要把输入拉到线性区，显然是错误的。

The issue with the above approach is that the gradient descent optimization does not take into account the fact that the normalization takes place.

但是我们为了达到加速训练的目的，就必须固定每一层的输入分布，即 whiten 是必须的。
因此，我们只能换一个思路：在梯度下降优化时，要考虑到 whiten 的执行过程，即修改梯度下降（参数优化）的方式。

要达到的最终效果是：

For any parameter values, the network always produces activations with the desired distribution.

2.2 梯度修正及其问题

现在我们考虑输入是多个向量 \(\mathbf x\) 的情况，它们的集合还是 \(\mathscr X\) 。

如果我们将 normalization 作为网络中的一个结构（一个步骤），那么就有：

\[\hat {\mathbf x} = Norm(\mathbf x, \mathscr X) \]

自变量包括 \(\mathscr X\) ，是因为标准化需要求均值和标准差。

那么当参数优化（梯度下降）时，我们需要同时计算：

\[\frac{\partial Norm(\mathbf x, \mathscr X)}{\partial \mathbf x}, \frac{\partial Norm(\mathbf x, \mathscr X)}{\partial \mathscr X} \]

这么一通操作以后，问题似乎解决了。实际上我们又遇到了两个致命问题：

• 向量标准化计算量非常大。我们需要对该向量集计算均值向量和协方差矩阵，还要求该矩阵平方根的逆矩阵！

• 反向求导时，上面两个偏导很难求啊！！！

因此，原始的标准化操作是不可取的，我们必须有替代方式！以下才是本文的核心方法！

BTW，前人的方法太过于简单，就是取一个样本，或者取若干张 feature map ，以简化计算。
显然这样做是不可取的，没有任何创新。

2.3 Key Algorithm

本文做了三点创新（简化）：

对向量中的每一个标量进行标准化

我们不再对输入向量进行统一操作（减去同一个均值向量，除以同一个矩阵），而是对输入向量的每个标量进行独立的标准化操作。
为什么，怎么做，继续看后面两点。

For a layer with d-dimensional input \(x = (x^{(1)} \cdots x^{(d)})\), we will normalize each dimension:

\[\hat x^{(k)} = \frac{x^{(k)} - E[x^{(k)}]}{\sqrt {Var[x^{k}]}} \]

where the expectation and variance are computed over the training data set.

Batch Normalizing Transform

为了保持网络的表达能力，本文提出了一个Batch Normalizing Transform。

我们不恢复 \(x^{(k)}\) （否则不就白标准化了嘛），但要提供网络自我学习 \(x^{(k)}\) 的能力。
因此，我们在原始网络的前面，在标准化以后，加上如下线性变换过程：

\[y^{(k)} = \gamma^{(k)} \hat x^{(k)} + \beta^{(k)} \]

其中参数：\(\gamma^{(k)}\)和\(\beta^{(k)}\)是网络自己学习得到的！

当然了，如果网络学习的结果是 \(\gamma^{(k)} = \sqrt {Var[x^{k}]}, \beta^{(k)} = E[x^{(k)}]\) ，那么就和 BN 操作前一样了。
但是，网络一般不会这么做。因此我们只是给网络提供了恢复表达能力的可能性，怎样迭代优化更理想，网络自己说了算。
最重要的是，对网络整体而言，它的输入是标准化的 \(\hat x^{(k)}\) ，那么训练就会很快！

完整变换流程如下：

正因为此，我们要逐个标量操作。

Mini-batch

第三点，既然梯度下降通常是以 mini-batch 的形式，那么前向传播中需要的均值和标准差，也由 mini-batch 计算得到就好了。

此时，反向传播变得非常简单！
首先， BN 变换是一个线性变化，求导简单；其次，我们是对标量操作的，不涉及协方差矩阵！

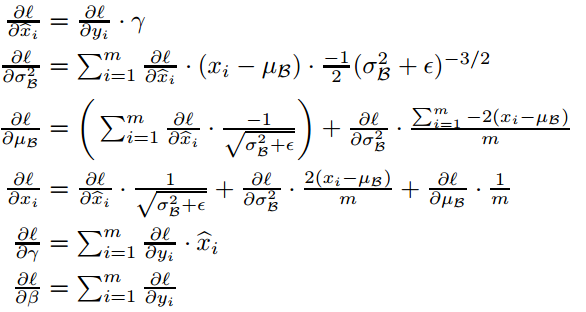
2.4 Inference

注意了，虽然在优化该层的时候，我们使用 mini-batch ，但如果是测试阶段，我们还是得使用整体输入。
即，当模型训练完成后， \(x\) 到 \(\hat x\) 的标准化必须计算全部输入的均值和标准差来完成。其中方差用的是无偏估计。

由于是全体输入，因此均值和标准差就是常数， BN 变换就可以看作是一个简单的线性变换（对输入向量的每一个标量而言，线性变换参数还是不同的）。

综上，含 BN 网络完整流程如下，上面是训练，下面是 inference ：

2.5 实际应用方式

如果某个网络中包含如下形式——仿射变换 + 非线性变换：

\[z = g(Wu+b) \]

那么我们就在非线性变换之前，即对 \(Wu+b\) 采用 BN 变换。原因是：

\(Wu+b\) is more likely to have a symmetric, non-sparse distribution, that is "more Gaussian" (Hyv¨arinen & Oja, 2000).

这种情况非常多，包括每一个全连接层的输出单元（除了最后一层），以及每个卷积层的输出单元。

如果我们想对 \(u\) 实施，那么由于 \(u\) 一般是上一层是输出，是随时变化的，因此效果不好。
所以我们都在每一层非线性输出前采用，效果最佳。

此外，对于卷积层，我们还希望在同一个 feature map 上， BN 变换的方式是一致的，否则卷积（模板匹配）效果就打乱啦。
为此，我们的 mini-batch 将以 feature map 为单位，一个 feature map 上所有节点的 \(\gamma^{(k)}\) 和 \(\beta^{(k)}\) 都是一致的。inference 同理。

3. EFFECT

BN method 使得我们可以:

• 采用更大的学习率；

• 不用太在意初始化。

在一些情况下，甚至充当了 regularizer ，因此我们可以用更少的 Dropout 。

运用在当时最优秀的图片分类器上，在相同准确率下，训练次数只有原来的 \(\frac{1}{14} (7\%)\) 。