机器学习中的范数正则化
机器学习中的范数正则化
使用正则化有两大目标:
- 抑制过拟合;
- 将先验知识融入学习过程,比如稀疏、低秩、平滑等特性。
结合第二点以及贝叶斯估计的观点,正则化项(regularizer)就是先验概率项。
监督学习中绝大多数任务都可以概括为以下最小化目标:
第一项损失函数我们在此不多说。如果是Square loss,那就成了最小二乘模型;如果是Hinge Loss,那就成了SVM模型;如果是exp-Loss,那就是牛逼的 Boosting;如果是log-Loss,那就是Logistic Regression。
我们重点看第二项。我们普遍用到的正则项涉及:零范数、一范数、二范数、迹范数、Frobenius范数和核范数等。那么它们各有什么作用呢?
1. \(l_0\)范数和\(l_1\)范数
首先,\(l_0\)范数是一个向量中非零元素的个数。
显然,如果我们将\(l_0\)范数用于参数矩阵的正则化,那么我们希望得到稀疏的参数矩阵。
实际上,任何规则化算子,只要在\(\mathbf{W} = 0\)处不可微,并且可以分解为一个“求和”的形式,那么该规则化算子就具有稀疏功能。
在实际应用中,我们一谈到稀疏,用的更多的是\(l_1\)范数。这其中是有原因的。
我们先来看看\(l_1\)范数。
\(l_1\)范数是一个向量中所有元素绝对值之和,又称为稀疏规则算子(Lasso regularization)。
实际上,\(l_1\)范数是\(l_0\)范数的最紧凸松弛(convex relaxation)。并且\(l_1\)范数具有更好的优化特性(\(l_0\)范数是NP难问题)。因此\(l_1\)范数应用得更广。
参考讲义,截图:

稀疏性有两大好处:
- 特征选择,避免噪声对额外特征的影响。
- 加强可解释性(interpretability)。
2. \(l_2\)范数
在回归问题中,有人又称之为岭回归(ridge regression),有人称之为权值衰减(weight decay)。其最常用目标是抑制过拟合。
百度百科对岭回归的概括非常精炼:
岭回归(ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
维基百科:
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, in machine learning it is known as weight decay, and with multiple independent discoveries, it is also variously known as the Tikhonov–Miller method, the Phillips–Twomey method, the constrained linear inversion method, and the method of linear regularization. It is related to the Levenberg–Marquardt algorithm for non-linear least-squares problems.
和\(l_1\)范数不同的是,\(l_2\)范数没有显式地要求元素等于0,而是要求所有元素综合较小。
关于这一点,我们还可以从数据分布上考虑,参见一篇博文。
这篇博文告诉我们,高斯分布先验对应\(l_1\)正则化,而拉普拉斯分布先验对应\(l_2\)正则化。高斯分布中小值较多,拉普拉斯分布中大值较多,因此\(l_1\)正则化的稀疏效果比\(l_2\)更强。
我们还可以举个例子:
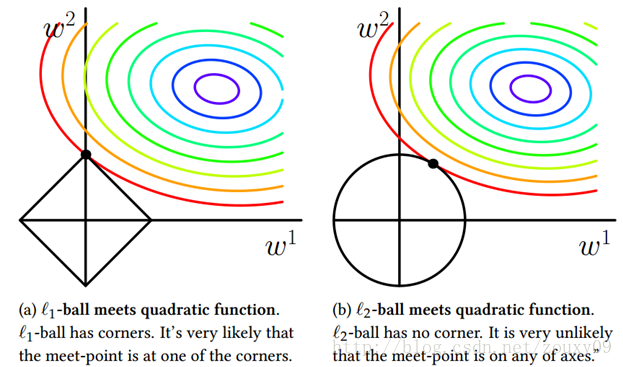
显然,\(l_1\)正则化的最优解常常发生在坐标轴上(稀疏);而\(l_2\)正则化的最优解则很难发生在坐标轴上。
因此通过\(l_2\)正则化,我们就能得到相对简单的参数,抑制模型拟合噪点或过拟合。
此外,\(l_2\)范数有一个特别的作用:可以解决病态矩阵求逆难的问题。
例如,当我们的样本数小于参数矩阵维度时,习得模型很容易发生过拟合。对于线性模型来说,此时的参数矩阵一定是不满秩的。因此逆矩阵不存在。
但当我们加入正则化项后,我们就可以直接求逆了。
最后,\(l_2\)范数还可以稳定和加快收敛过程。
\(l_2\)范数正则项的加入,可以使目标函数具有\(\lambda\)-强凸(strongly-convex)的性质。
见下图:

图右为一般凸函数,要求每一点都处于其一阶泰勒函数的上方;而图左的\(\lambda\)-强凸更进一步,要求其每一点都存在一个非常漂亮的二次下界(quadratic lower bound)。
显然,图左在接近局部极小值点时仍然能保持较高的收敛速度。
3. 核范数(nuclear norm)
核范数是用来引导低秩(low-rank)特性的。其定义为奇异值之和。
实际上,我们的最初目标是让参数矩阵秩最小。可惜的是,rank和\(l_0\)范数一样都是非凸的。而rank函数的最佳凸估计/ 松弛就是核范数。
核范数正则化有很多妙用,无外乎都涉及到低秩特性或先验。
-
矩阵填充(matrix completion)
比如我们要做一个影片推荐系统。由于参数量非常大,因此总会有缺失的参数,比如某个用户并没有标出喜欢的演员、历史看过的影片,或是遇到了刚上映的影片。
这时,我们就要通过一些手段恢复这一参数矩阵,从而进行推荐。其中一个重要的限制就是低秩性,因为人和人之间总是有共性的。 -
背景建模
假设我们要从一个固定相机拍摄的视频序列的每一帧中,分离背景和目标(前景)。
其中一个思路是:我们将每一帧的所有像素都拉成一个列向量;多帧列向量就组成了一个矩阵。
其中,由于背景是比较稳定的,因此背景矩阵的秩比较低。
此外,由于前景所占像素通常较少,因此前景矩阵具有稀疏性。
那么,总的视频矩阵就是由这两个矩阵叠加而成。如果我们想恢复背景,那么就要尝试从中重建出低秩矩阵。
-
健壮PCA
我们回顾一下PCA方法。PCA方法希望用一组正交基向量表示空间中的向量\(\vec{x}\),使其截断估计时均方误差最小。
以人脸图片为例。人脸图像中,噪声是稀疏的,而人脸由于具有对称性和自相似性,因此是低秩的。
因此我们的优化目标可以是:\[\min_{\mathbf{A},\mathbf{E}} {\Vert \mathbf{A} \Vert_* + \lambda \Vert \mathbf{E} \Vert_1}, s.t. \mathbf{X} = \mathbf{A} + \mathbf{E} \]原理就是上面说的,因为\(l_0\)范数和rank函数都是非凸、非光滑的,因此转为求它们的最优凸近似(松弛):\(l_1\)范数和核范数。
在实际操作中,我们可以将同一个人的多幅照片组成一个矩阵,从而解决这多幅照片中存在的遮挡、噪声、光照等问题。如图:
-
变换不变低秩纹理(TILT)
实际上,作为一副二维图像,其本身就存在较强的对称性和自相似性,远远不止上面方法所说的像素相似性。
假设我们定义了某种对称性,并以此考量矩阵的秩。若对称性十足,那么图像的秩就会很低(列向量相似性很高)。
但是,如果图像存在几何变形,则低秩性就会被破坏。
TILT正是从这个思路出发,完成图像的几何校正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号