贝叶斯估计和极大似然估计到底有何区别
个人理解:
最大似然估计:只是对似然的处理,概率乘积转概率密度乘积,取对数转加,求导得估计值;
贝叶斯估计:由先验乘似然得后验,
这个就是贝叶斯学习过程:在前一个训练集合的后验概率
上,乘以新的测试样本点
的似然估计,得到新的集合
的后验概率
,这样,相当于
成为了
的先验概率分布:
;
原文:https://blog.csdn.net/feilong_csdn/article/details/61633180
预热知识必知
如何求类条件概率密度:
我们知道贝叶斯决策中关键便在于知道后验概率,那么问题便集中在求解类条件概率密度!那么如何求呢?答案便是:将类条件概率密度进行参数化。
最大似然估计和贝叶斯估计参数估计:
鉴于类条件概率密度难求,我们将其进行参数化,这样我们便只需要对参数进行求解就行了,问题难度将大大降低!比如:我们假设类条件概率密度p(x|w)是一个多元正态分布,那么我们就可以把问题从估计完全未知的概率密度p(x|w)转化成估计参数:均值u、协方差ε
所以最大似然估计和贝叶斯估计都属于参数化估计!……当然像KNN估计、Parzen窗这些就是非参数话估计啦!但是参数化估计也自然有它的缺点,下面会说的!
简述二者最大的区别
若用两个字高度概括二者的最大区别那就是:参数
最大似然估计和贝叶斯估计最大区别便在于估计的参数不同,最大似然估计要估计的参数θ被当作是固定形式的一个未知变量,然后我们结合真实数据通过最大化似然函数来求解这个固定形式的未知变量!
贝叶斯估计则是将参数视为是有某种已知先验分布的随机变量,意思便是这个参数他不是一个固定的未知数,而是符合一定先验分布如:随机变量θ符合正态分布等!那么在贝叶斯估计中除了类条件概率密度p(x|w)符合一定的先验分布,参数θ也符合一定的先验分布。我们通过贝叶斯规则将参数的先验分布转化成后验分布进行求解!
同时在贝叶斯模型使用过程中,贝叶斯估计用的是后验概率,而最大似然估计直接使用的是类条件概率密度。
下面会详细分析最大似然估计和贝叶斯估计求解模型!
从其他方面谈谈二者的异同
在先验概率能保证问题有解的情况下,最大似然估计和贝叶斯估计在训练样本趋近于无穷时得到的结果是一样的!但是实际的模式识别问题中,训练样本总是有限的,我们应如何选择使用哪种模型呢?下面简单分析分析:
(1) 计算复杂度:就实现的复杂度来说,肯定是有限选择最大似然估计,最大似然估计中只需要使用到简单的微分运算即可,而在贝叶斯估计中则需要用到非常复杂的多重积分,不仅如此,贝叶斯估计相对来说也更难理解;
(2)准确性:当采用的样本数据很有限时,贝叶斯估计误差更小,毕竟在理论上,贝叶斯估计有很强的理论和算法基础。
参数化估计的缺点:
贝叶斯估计和最大似然估计都是属于参数化估计,那么二者存在着一个共同的缺点:参数化估计虽然使得类条件概率密度变得相对简单,但估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。在现实应用中,与做出能较好的接近潜在真实分布中的假设,往往需要一定程度上利用关于应用任务本身的经验知识,否则若仅凭“猜测”来假设概率分布形式,很可能产生误导性的结果!所以没有什么算法是十全十美的啦!
下面便推导一下最大似然估计和贝叶斯估计所使用的模型,最大似然简单些,贝叶斯估计就比较复杂了!
最大似然估计模型推导
假设样本集D={x1 、x2 、…、xn},假设样本之间都是相对独立的,注意这个假设很重要!于是便有:
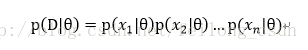
所以假设似然函数为:
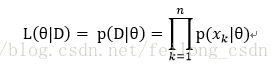
接下来我们求参的准则便是如名字一样最大化似然函数喽:
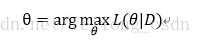
下面有一个优化,专业名词为拉布拉斯修正
简单说:就是防止先验概率为0,那么上面的L(θ|D)整个式子便都成0 了,那肯定是不行的啊,不能因为一个数据误差影响了整个数据的使用。同时那么多先验概率相乘,可能出现下溢出。所以引入拉普拉斯修正,也就是取对数ln,想必大家在数学中都用过这种方法的。
所以做出下面变换:
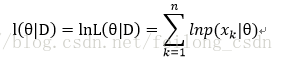
所以最大化的目标便是:
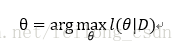
求解上面问题便不多说了,使用数学中的微分知识便可:
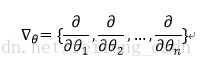
然后使得偏导数为0:
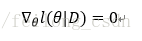
自此便求出了参数θ,然后便得到了类条件概率密度,便可进行判别等接下来的工作了。
下面讲解贝叶斯模型推导,略微复杂些,下伙伴们仔细看啊!
贝叶斯估计模型推导
先说一句,贝叶斯估计最终也是为了得出后验概率。所以贝叶斯最终所要的得到推导的是:
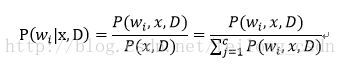
正如上面所说我们便是要参数的先验分布通过贝叶斯规则转化成后验概率,也就是上面这个公式,接下来我们一起看看如何推导出上面后验概率的公式通过参数的先验概率。
上式中有:
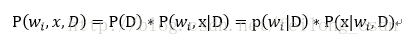
带入后验概率的式子可得:
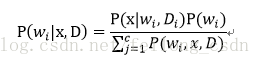
大家注意啦!!!这里也有个重要的假设,那就是样本之间是相互独立的,同时类也是相互独立的。所以有如下假设:
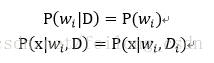
同时由于类之间相互独立,所以我们不用区分类了,便有:
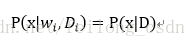
这里给大家顺一下思路,所以我们要求后验概率便是要求出P(x|D)便可:
下面说明P(x|D)的推导:
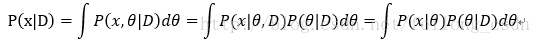
正如我们前面所说上式中p(x| θ),我们假设它是一个已知的满足一定先验分布的,我们现在便是要知道:
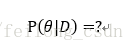
下面给出其推导过程:
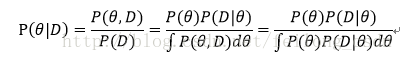
对于上式中的P(D|θ),还记得上面说的很重要的样本之间是独立的吗,所以和最大似然函数类似有:
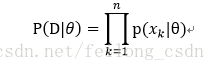
因此最终我们便可以求得P(x|D):
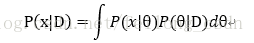
这样我们将P(x|D)待会后验概率的式子便可求出后验概率了,所以我们完成了上面的说法,便是将参数θ 服从的先验概率分布转化成了后验概率分布了。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号