DFS总结
常见剪枝方法
- 优化搜索顺序
优先搜索决策树较小的点,例如在165. 小猫爬山一题中,优先搜索体重较大的扩展出的情况较少 - 排除冗余信息
如果某些情况在此前已经被搜索过了,那么无需继续搜索 - 可行性剪枝
如果可以证明某些情况已经无法得到答案了,那么无需继续搜索 - 最优性剪枝
如果某些情况的当前最优解已经偏离答案了(例如要求最小值,但当前维护的答案已经大于全局最小值),那么无需继续搜索注:停止搜索的前提是必须保证继续搜索会距离答案越来越远,某些情况下当前偏离答案不代表最终不能成为答案
迭代加深
算法介绍
迭代加深是一种限制搜索搜索深度的DFS
应用场景
使用迭代加深的场景一般满足具有以下几点特征:
- 搜索树中某些分支层数较多,某些分支层数较少
- 分支层数较多的分支位于分支层数较少的分支前
- 答案存在于分支层数较少的分支中
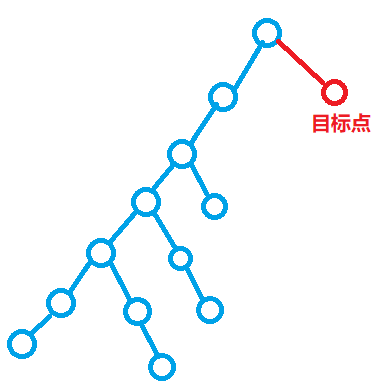
实际做题时如何判断是否要使用迭代加深?
比较一下最坏情况下的搜索层数和答案所在的层数,若两者相差较大则可能可以采用迭代加深
思路
由上图可知,如果按照常规DFS的策略,会首先把第一条分支搜到底,然后才会搜索到目标点,然而第一条分支的层数过深,可能导致超时。因此考虑以下策略:
a. 规定一个最大搜索层数,当搜索层数超过规定值时停止向下层继续搜索,返回并对其他分支展开搜索
b. 当前搜索层数全部搜索完成后如果未找到解则加大搜索层数重复过程a再次进行搜索
c. 重复过程a和b直到找到目标
迭代加深只不过提供了一种新的搜索的顺序以应对一些情况,实际思考过程仍应当以普通搜索入手,若发现具有以上几点特征则可以考虑采用迭代加深更改搜索顺序
优点
- 规定最大层数,可以避免首先搜索一些较深的搜索分支时带来的超时问题
- 相比于将一层中的所有点载入队列再逐个搜索的\(O(n^2)\)的
BFS,在规定最大搜索层数之后的搜索过程中采用\(O(n)\)前进策略的DFS,在面对一些多叉树问题时,具有更高的效率
例题
分析
首先确定待搜索内容为每个位置应当填写的数值
从常规DFS的角度思考,我们可以去搜索每一组可行序列,但是并不能确定当前的可行序列一定为最短的序列,因此需要搜索出所有可行序列从中选取最短
可以发现,最坏情况下搜索的深度为100,即1,2,3,...,100,这样所带来的无效搜索分支比较庞大
同时可以发现,答案的深度一般比较小,对于128而言,仅需要1, 2, 4, 8, 16, 32, 64, 128,即答案对应的搜索层数比较小
因此考虑采用迭代加深,每次搜索前设定最大搜索层数depth,当搜索到depth层时不再向下层搜索,判断是否构成合法序列
若到达depth层的搜索空间中不包含答案,则扩大搜索层数为depth+1继续上述过程
重复以上过程直到找到答案
代码实现
// 常规dfs,确定每个位置应当填写的数值
// 由于dfs只能去搜索可行解,而不能确定当前解是否为最终解,即当前的长度未必是最短的,后续可能有更短的序列,因此需要搜索所有情况维护最短序列
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>
using namespace std;
constexpr int N = 110;
constexpr int INF = 0x3f3f3f3f;
int res[N]; // 记录答案
int path[N], cnt; // 记录中间过程
int minStep; // 可行序列的最短长度
void dfs(int u, int n) {
bool st[N] = {0};
if (u >= minStep) return;
if (path[u - 1] == n) {
if (u < minStep) {
minStep = u;
memcpy(res, path, sizeof path);
}
return;
}
for (int i = 0; i < u; ++i)
for (int j = i; ~j; --j) {
int s = path[i] + path[j];
// 1. 比最大值大 s > n0000
// 2. 不能保证严格递增 s <= path[u - 1]
// 3. 已经搜索过了 st[s]
// 以上情况不需要再搜索了
if (s > n || s <= path[u - 1] || st[s]) continue;
st[s] = true;
path[cnt++] = s;
dfs(u + 1, n);
--cnt;
// st不需要还原的原因
// st标记的是对于下面这种情况
// path[0]->path[3]依次为1 2 3 4
// 在搜索dfs(5, n)时,1+4 == 2+3,如果不标记就会搜索2次5,显然这2次是重复的
// 我最开始担心的是对于 1 2 3 5 和 1 2 4 5,如果在1 2 4 5时把5标记了,那么1 2 3 5这种情况就会直接忽略了
// 但是1 2 4 5 和 1 2 3 5是两种情况,在进入5这一层时st都会初始化为全0
}
}
void solve(int n) {
path[cnt++] = 1;
dfs(1, n);
for (int i = 0; i < minStep; ++i) cout << res[i] << ' ';
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n;
while (cin >> n, n) {
minStep = INF;
cnt = 0;
solve(n);
}
return 0;
}
// 上述过程之所以需要搜索所有情况是因为我们无法确定最短的合法序列长度是多少
// 所以还有一种思路是枚举最短的合法序列长度,在规定的长度内判断是否存在解
// 迭代加深在本题中并没有很好的体现,因为迭代加深似乎是应对一些特殊情况所指定的一种搜索顺序,但是在本题中枚举最短合法序列长度似乎属于正常解题思路
// 不过本题是符合迭代加深的特征的,因为目标是搜索合法序列,一些合法序列的层数确实较深,因此首先规定搜索层数
// 但是规定搜索层数这个操作如果不看为迭代加深的过程,是可以作为另一种解题思路的,所以这道题就没有明显的体现出迭代加深的独特应用来
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>
using namespace std;
constexpr int N = 110;
constexpr int INF = 0x3f3f3f3f;
int n;
int path[N];
// u:当前搜索层数 depth:最大限度搜索层数
bool dfs(int u, int depth) {
// 以下两种写法均可以获得正确答案,但是前者在path[u - 1] != n时在depth层未必会return,需要到下一层才会返回,效率会差一些
// 实际上一个搜索分支在到达depth层时,就已经可以判断该路径是否为合法路径了,直接返回即可
// if (u > depth) return false;
// if (path[u - 1] == n) return true;
if (u == depth) return (path[u - 1] == n);
bool st[N] = {0};
for (int i = 0; i < u; ++i)
for (int j = i; ~j; --j) {
int s = path[i] + path[j];
if (s > n || s <= path[u - 1] || st[s]) continue;
st[s] = true;
path[u] = s;
if (dfs(u + 1, depth)) return true;
}
return false;
}
void solve(int n) {
bool st[N] = {0};
int depth = 1;
path[0] = 1;
while (!dfs(1, depth)) ++depth; // 限定最深层数为depth,如果未找到解则加深层次继续搜索
for (int i = 0; i < depth; ++i) cout << path[i] << ' ';
cout << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
while (cin >> n, n) solve(n);
return 0;
}
双向DFS(折半搜索)
算法原理
双向DFS减少搜索空间的原理和双向BFS是相同的,这里不再赘述
双向DFS的实现方式是将序列分为2部分,分别进行DFS。在某些情况下,即使将搜索结果分开但是并不影响和的求解,例如对于一个序列的搜索结果为1, 2, 3, 4,目标是求解它们的和,如果分开计算1+2和3+4,再将两部分的和合并,显然与直接计算1+2+3+4的结果是一样的。
双向DFS就是利用这种拆分后结果不变性,将具有较大搜索空间的长序列拆分为各自具有较小搜索空间的短序列,再对结果进行合并
注:应用折半搜索的前提是能够对拆分后各个部分的搜索结果进行正确合并,使用时一定要保证这一点
例题
解题思路
将所有礼物分为2部分,首先预处理第1部分各个选法的重量和,之后枚举另一部分的各个选法,通过二分在第一部分预处理结果中找到<=最大重量限制-第2部分重量且最大的值,两者之和即为一个合法解,维护合法解的最大值即为答案
时间复杂度
礼物总个数为\(n\),设第1部分的礼物数为\(k\),则第2部分的礼物数为\(n-k\),
第1部分每个礼物要么选要么不选,因此总数为\(2^k\),
第2部分搜索部分的总数为\(2^{n-k}\),但是每一个状态都需要对第1部分进行一次二分查找,所以复杂度为\(2^{n - k} * log_2{2^k}\),即\(2^{n - k} * k\)
因此整体复杂度为\(2^k + 2^{n - k} * k\)
根据基本不等式可知,在\(2^k\) 和 \(2^{n - k} * k\) 尽可能接近时,两者的和较小
因此在本题中,\(k\)取\(25\)会比取\(23\)具有更优的复杂度
代码实现
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>
using namespace std;
constexpr int N = 50;
constexpr int INF = 0x3f3f3f3f;
int n, m; // n个物品,最大搬动重量为m
int w[N]; // 每个物品重量
int weight[(1 << 23) + 10], cnt; // 对第1部分的各个选法,预处理出其重量和,注意数组大小
int res;
// 对第1部分的预处理
void dfs1(int u, int s, int k) { // 当前搜索第u个物品,当前总重量为s,需要搜索到第k个物品
if (u == k) {
weight[cnt++] = s;
return;
}
dfs1(u + 1, s, k); // 不拿第u个物品
if (w[u] <= m - s) dfs1(u + 1, s + w[u], k); // 拿第u个物品
}
// 对第2部分进行dfs
void dfs2(int u, int s, int k) {
if (u == k) {
int l = 0, r = cnt - 1; // 去weight中二分查找目标值
while (l < r) {
int mid = (l + r + 1) >> 1;
if (weight[mid] <= m - s) l = mid;
else r = mid - 1;
}
if (weight[l] <= m - s)
res = max(res, s + weight[l]);
return;
}
dfs2(u + 1, s, k); // 不拿第u个物品
if (w[u] <= m - s) dfs2(u + 1, s + w[u], k);
}
void solve() {
cin >> m >> n;
for (int i = 0; i < n; ++i) cin >> w[i];
// 优化搜索顺序,优先枚举大的会减少搜索分支数量
sort(w, w + n, [](int a, int b) -> bool {return a > b;});
int k = n >> 1;
dfs1(0, 0, k);
sort(weight, weight + cnt); // 由于第2部分在dfs时需要对weight进行二分查找,需要排序
res = 0;
dfs2(k, 0, n);
cout << res << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
solve();
return 0;
}
IDA*
算法介绍
IDA*的全称为:Iterative deepening A*,即基于迭代加深的A*算法
A*算法估价函数的引入,可以看为对迭代加深进行的又一步剪枝
算法原理
在迭代加深代码框架基础上,对每个状态点引入一个估价值(该点距离目标点所需的最小步数),如果某状态点的深度加上该点的估价值>迭代加深限制的最大层数则直接返回不再向下层继续搜索
同A*算法一样,都需要保证估价值 <= 真实值
该算法的难点仍在于如何确定估价函数
例题
注:由于不同题目确定估价函数的方式各不相同,这里的题目仅是给出一个应用实例,无法做出推广
分析
首先从 \(1 \leq n \leq 15\) 较小的数据范围可以推知本题可以采用搜索来解决
无论迭代加深还是A*,本质上都是对于常规DFS的一种优化,在考虑问题时,我们只需要从常规搜索入手
由于题目是对于连续的一段进行操作,因此考虑枚举操作段的长度
设当前操作段长度为\(k\),则可选操作段数量为\(n - k + 1\),剩余元素数量为\(n - k\),
该操作段可选择的移动目标位置有\(n - k + 1\)种(\(n - k\)个元素有\(n - k + 1\)个空隙),除去当前位置,还剩余\(n - k\)个可选位置,
因此操作段长度为\(k\)时的方案数为\((n - k + 1) * (n - k)\),但是要考虑这其中包含重复的情况,例如序列 1 2 3 4,将 1 2 放到 3 4 后和将 3 4 放到 1 2 后等价的,因此操作段长度为\(k\)时的方案数为\(\frac{(n - k + 1) * (n - k)}{2}\),因此操作所有长度的\(k\)的方案数总和为\(\sum\limits_{k=1}^{15}\frac{(n - k + 1) * (n - k)}{2}\)
题目规定最多进行\(4\)步操作,每步操作可选方案为\(\sum\limits_{k=1}^{15}\frac{(n - k + 1) * (n - k)}{2}\),根据\(\sum\limits_{i=1}^{n}(i * (i + 1)) = \frac{n * (n + 1) * (n + 2)}{3}\),可得每步操作可选方案为\(560\)种。因此对于常规搜索,一共需要搜索\(560^4=98344960000\)次,是会超时的。
可以选择通过双向BFS或IDA*来解决,下面分析一下本题中估价函数的设计方法
对于一个最终序列,例如1 2 3 4 5 6,一个很明显的特征是前一个数总比后一个数小\(1\),我们称其为前后关联性
如果将2 3移动到5之后转变为1 4 5 2 3 6,前后关联性收到影响的点为1,3,5,可以发现每移动一段区间,前后关联性收到影响的点数均为3
换言之,如果当前前后关联性不满足条件(后数-前数=\(1\))的点数为\(3\),则还需要操作的次数至少为\(\frac{3}{3} = 1\)次,实际可能的操作次数是\(>=1\)次的,这恰恰符合估价值和实际值之间的关系
设不符合前后关联性的点数为\(tot\),则\(\lceil \frac{tot}{3} \rceil(\lfloor \frac{tot + 2}{3} \rfloor)\)作为估价值恰好可以满足各项要求
之后在迭代加深代码框架的基础上,维护估价函数并应用于搜索过程。具体细节见代码实现。
代码
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>
using namespace std;
constexpr int N = 20;
constexpr int INF = 0x3f3f3f3f;
int n;
int a[N];
int t[10][N];
inline int f() { // 计算估价函数
int cnt = 0;
for (int i = 0; i < n - 1; ++i)
if (a[i] != a[i + 1] - 1) ++cnt;
return (cnt + 2) / 3;
}
bool dfs(int depth, int max_depth) { // 当前已经操作depth步,最大操作max_depth步
if (!f()) return true; // 估价值为0时已经到达目标状态
if (depth + f() > max_depth) return false; // 如果当前还没有到达终点并且当前搜索层数加上剩余估计待搜索层数已经超过限定值则直接返回
for (int len = 1; len <= n; ++len) // 枚举连续区间的长度
for (int l = 0; l + len - 1 < n; ++l) { // 枚举连续区间起点
int r = l + len - 1;
// 将序列[l, r]变动位置
// 对于1 2 3 4 5 6,将4 5放到2前面<=>将2 3放到5后面,即后面序列在移动位置时,目标位置只需要考虑该序列后面的
for (int k = r + 1; k < n; ++k) { // 依次考虑将[l, r]放置到a[k]...a[n]的后面
// 本次移动后,下次需要恢复现场,因此需要辅助数组
// 此时需要考虑此时进行的是递归操作,是否每层都需要开辅助数组,不同层之间是否会相互影响。显然是有影响的,当前层的搜索状态在进入到下层搜索时不应当被修改
memcpy(t[depth], a, sizeof a);
// 把[l, r]放置到a[k]的后面
for (int x = r + 1, y = l; x <= k; ++x, ++y) a[y] = t[depth][x]; // [r + 1, k] -> [l, k-r-1+l]
for (int x = l, y = k - r + l; x <= r; ++x, ++y) a[y] = t[depth][x]; // [l, r] -> [k-r+l, k]
if (dfs(depth + 1, max_depth)) return true;
memcpy(a, t[depth], sizeof a);
}
}
return false;
}
void solve() {
cin >> n;
for (int i = 0; i < n; ++i) cin >> a[i];
// int depth = 1; // 初始限制只能操作1步
int depth = 0; // 在搜索到目标序列返回时采用depth作为答案,因此它除了限制的最大深度的含义外应当还有操作步数这一含义,初始值为0
// depth==0时表示此时已经操作0步,等于4时表示已经操作4步,在>=5时才需要停止
while (depth < 5 && !dfs(0, depth)) ++depth;
if (depth == 5) cout << "5 or more" << endl;
else cout << depth << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int T;
cin >> T;
while (T--) solve();
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号