网络流复习笔记
网络流
一些基础定义
什么是网络流?我们不妨把它想象成输水系统。
输水系统的源头是个大水库,能够提供无限量的水,终点站是 NFLS,从水库到 NFLS 要经过一些中转站,这些中转站之间用管道相连接。当然,管道不能运输无限量的水,不然管子就要爆掉了。
由于管子的粗细、长短可能不同,它能运输的最大水量也不一定相同。并且对于所有中转站,你流入多少水它就会流出多少水。不可能出现流入的水量比流出的水量多或者流出的水量比流入的水量多的情况。
如果把中转站转化为点,管道转化为边,那么就可以得到网络流的模型。
形式化地说,一个网络是一张有向图,它的每条边 \((x,y)\in E\) 都有一个边权 \(c(x,y)\),称为容量,也就是上文中所说的”运输的最大水量“。图中还有两个特殊点 \(S,T\),分别被称为源点(也就是上文中的水库)和汇点(也就是上文中的 NFLS)。
现在定义网络的流函数 \(f(x,y)\),它有以下性质:
- \(f(x,y)\leq c(x,y)\),也就是管道中实际运输的水量不能超过它运输的最大水量。
- \(f(x,y)=-f(y,x)\)
- 对于任意 \(x\neq S,x\neq T\),\(\sum\limits_{(u,x)\in E}f(u,x)=\sum\limits_{(x,v)\in E}f(x,v)\),也就是对于所有中转站,你流入多少水它就会流出多少水。
现在对于某个合法流函数 \(f(x,y)\),给出以下定义:
- 对于 \((x,y)\in E\),定义这条边的实际流量为 \(f(x,y)\),也就是实际流过去了多少水。定义剩余流量为 \(c(x,y)-f(x,y)\),也就是最多还能再流过去多少水。
- 定义一个网络的流量为 \(\sum\limits_{(S,u)\in E}f(S,u)\),也就是总共流出去了多少水。
最大流
对于一个给定的网络,使整个网络的流量最大的合法的流函数被称为网络的最大流,此时的流量被称为网络的最大流量。
对于一个给定的网络,求出其最大流是网络流里最常见也最基础的题型。求最大流算法有很多种,其中一类叫做增广路算法,基于最大流最小割定理不断找增广路求解。
EK 算法
先考虑一个最原始的贪心:对于当前网络,任意找一条 \(S\to T\) 的路径,使得路径上每条边的剩余流量都非零(我们称之为增广路)。记 \(mn\) 为这条路径上所有边的剩余流量的最小值。并将这条路径上所有边的流量都扣掉 \(mn\)。
我们模拟一下这个算法的过程,譬如有如下一张网络:
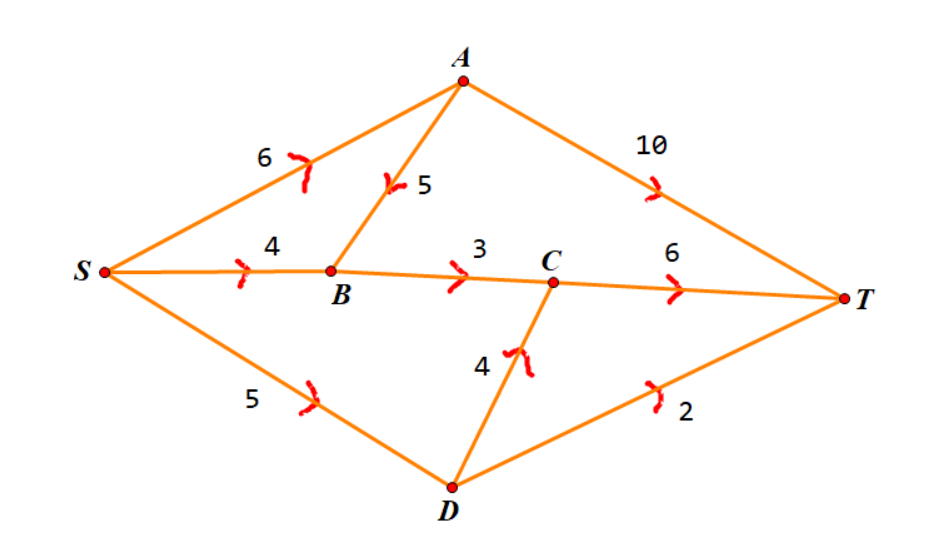
我们选择了 \(S\to A\to B\to C\to T\) 的增广路,并将其流量都加上 \(3\),也就是将其剩余流量都扣掉 \(3\),可得下图:
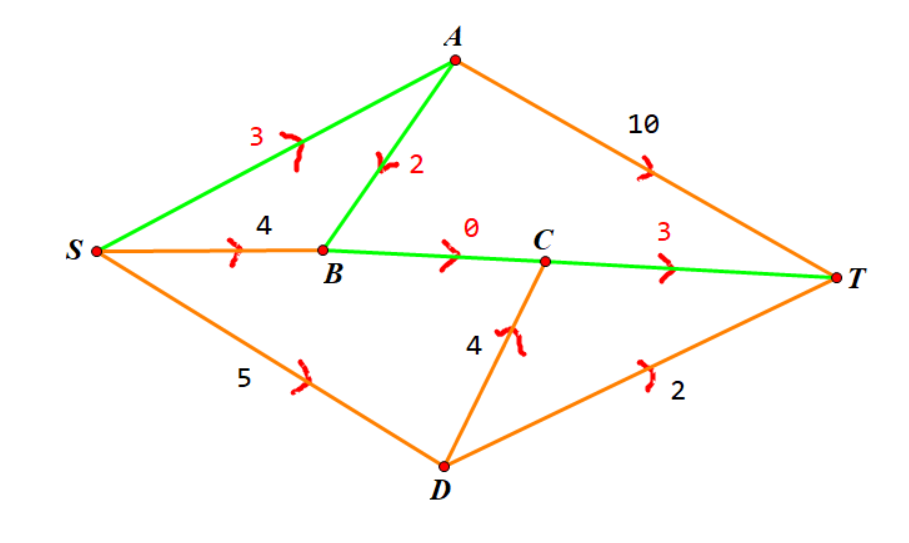
接下来几轮依次选择 \(S\to A\to T\),\(S\to D\to T\),\(S\to D\to C\to T\) 这三条增广路,依次可获得 \(3,2,3\) 的流量,最终一共可得 \(11\) 的流量。此时已无多余的增广路,残余网络如图所示:
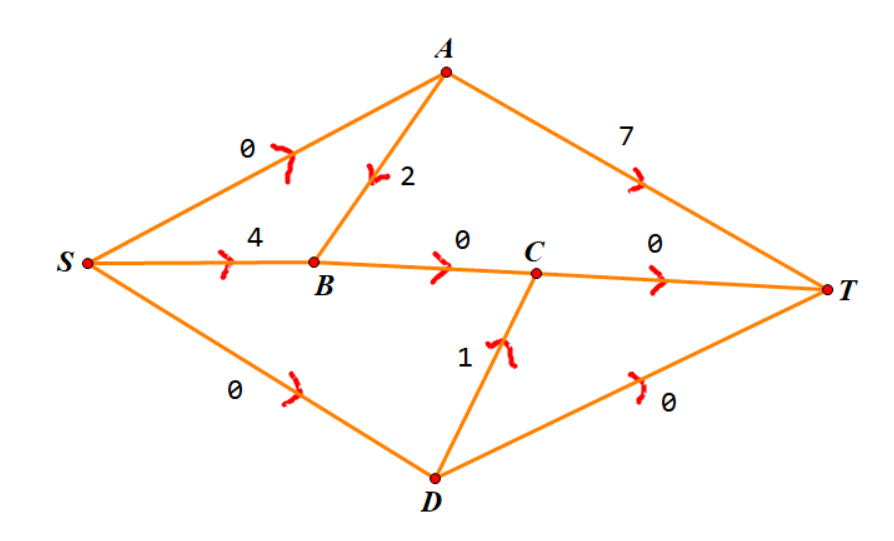
但非常抱歉,这个贪心是错误的。如果你一开始运气好依次选择 \(S\to B\to C\to T\),\(S\to A\to T\),\(S\to D\to T\),\(S\to D\to C\to T\) 这四条增广路,那么你依次可以获得 \(6,3,2,3\) 的流量,它们的总和为 \(14\)。
那么有什么补救方法呢?
考虑有个东西叫”反悔贪心“,我们对每条边 \(e=(x,y)\) 另减一条虚拟边 \(\bar{e}=(y,x)\),\(\bar{e}\) 的初始容量为 \(0\)。当 \((x,y)\) 中流过 \(f\) 的流量,就令 \(e\) 的容量减去 \(f\)(也就是 \(e\) 的剩余流量少了 \(f\)),再让 \(\bar{e}\) 的容量加上 \(f\),对新图求增广路就行了。
为什么?
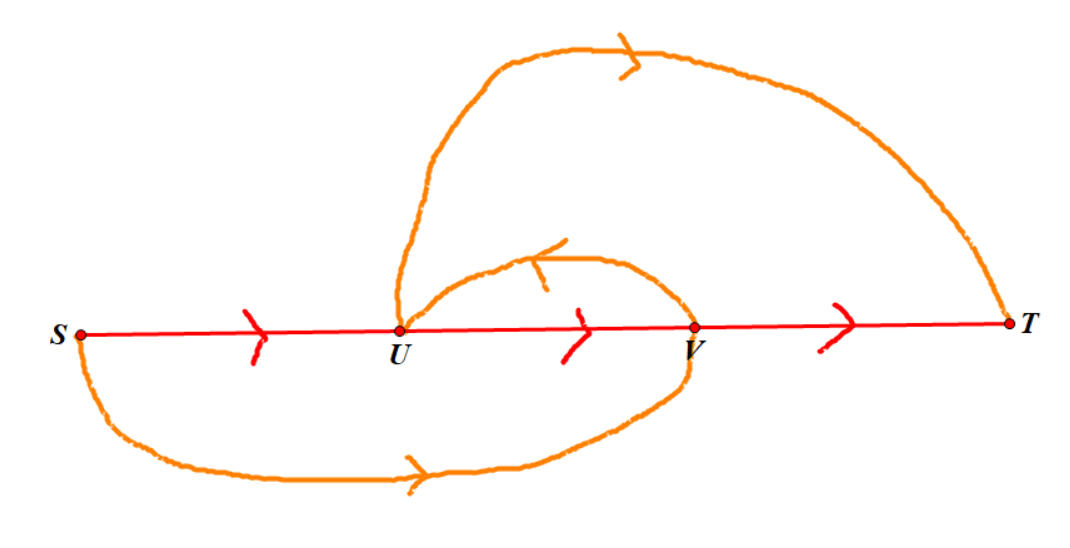
我们现在已经找出了一条 \(S\to T\) 的增广路(图中的红色部分),流过去了 \(a\) 的流量,这会导致这条增广路上的 \(\bar{e}\) 的容量增加了 \(a\),也就是我们重新求增广路的时候,会遇到某些边的反边。
假设我们又找出了一条增广路(图中的橙色部分),流过去了 \(b\) 的流量,令 \(\bar{e}\) 为这条橙色增广路上第一个为原图中某条边 \(e=(u,v)\) 的反边的边。(注:这个符号是我自己发明出来的)
考虑重新分配一下这两次流过去的流量,我们令第一条增广路流过去的流量由 \(a\) 变为 \(a-b\),再令 \(S\to v\to T\) 流过 \(b\) 的流量,以及 \(S\to u\to T\) 流过 \(b\) 的流量。
这样我们就成功避开了 \(\bar{e}\),并构造出了一个等价的可行流。
如果 \(u\to T\) 的路径上还经过原图上某条边的反边怎么办呢?那就重复一遍上面的操作,直到该路径不经过原图上某条边的反边。
由于 \(\bar{e}\) 有容量限制 \(a\),故第二次流过的流量 \(b\) 一定满足 \(b\leq a\),所以我们这样退流是没问题的。
也就是说,经过反向边的增广路我们都可以把它规约为不经过反向边的增广路。
上面的东西感性理解一下即可,u1s1 wll 里面有不少东西需要你感性理解呢。
接下来要证明的一个问题就是,为什么一直不断地增广,直到不能增广为止得到的流就是最大流。这个倒要给个严谨的证明。
对于给定的网络 \(G=(V,E)\),你随便选择两个点集 \(A,B\) 满足 \(A\cap B=\empty,A\cup B=V\),并且 \(S\) 属于 \(A\),\(T\) 属于 \(B\),我们称这样的 \(A,B\) 为 \(G\) 的一种割。记 \(P=\sum\limits_{u\in A,v\in B}f(u,v)-\sum\limits_{u\in A,v\in B}f(v,u)\)(即正向割边流量与负向割边流量的差),\(R=\sum\limits_{u\in A,v\in B}c(u,v)\)。
对于一个 \(G\) 的一个流,我们都有它的其流量 \(=P\)。
证明:考虑对 \(G\) 进行增广,假设其有一条增广路经过 \(v_1=S,v_2,\dots,v_k=T\) 这 \(k\) 个点,增加了 \(f\) 的流量。对于 \(v_i\in A,v_{i+1}\in B\),边 \((v_i,v_{i+1})\) 应属于这种割的正向割边,对 \(P\) 产生 \(+f\) 的贡献。而对于 \(v_i\in B,v_{i+1}\in A\),边 \((v_i,v_{i+1})\) 应属于这种割的负向割边,对 \(P\) 产生 \(-f\) 的贡献。并且由于最终 \(S\in A\),\(T\in B\),故 \(+f\) 贡献次数应当比 \(-f\) 贡献次数多 \(1\),故一次增广会对 \(P\) 产生 \(f\) 的贡献。而这个流的流量就是把每次增广增加的流量 \(f\) 加起来。故原命题得证。
而又显然 \(P\leq R\)。
故原图任意一个流的大小 \(\leq\) 任意一个割中正向割边的容量之和。
下面证明为什么它能达到”不能增广为止“这个状态。这部分还是相对比较简单的。你把所有边都割了 \(S\) 和 \(T\) 肯定不连通,也就是说最大流的大小一定不会超过所有边权值和。
考虑反证法,我们进行了无限次操作还是可以继续增广下去。由于我们每次增广新流过的流量都是正数——哪怕你每次只能流过 \(1\) 的流量。经过无限轮就可以得到无限的流量,而可行流的大小是有上界的(OI 中我们不考虑容量为 \(\infty\) 的情况,即便出现我们也可以用某个足够大的数如 0x3f3f3f3f 替代),故不可能增广无限次。也就是说该算法是不会陷入死循环的。
最后证明达到”不能增广为止“这个状态时网络的流量达到最大值。记 \(A\) 为增广到当前状态为止,剩余流量为 \(S\) 能到达的点,\(B=V-A\),显然 \(A,B\) 组成了 \(G\) 的一个割。
根据之前的推论,此时网络中的流量应当等于该割中正向割边与反向割边流量的差。
而显然正向割边的流量就等于其容量,负向割边的流量为 \(0\)。
故此时流量 \(=\) 此割中正向边的容量之和。
所以此时流量达到最大值。
上述证明过程同时也证明的最大流 \(=\) 最小割的定理。
upd on 2021.1.30:
很多人会误解割的定义。我们对于割的最原始的定义是将 \(V\) 划分成两个不相交的集合 \(A,B\),使得 \(S\in A,T\in B\)。并在此基础上定义了割的权值为 \(\sum\limits_{u\in A,v\in B}c(u,v)+\sum\limits_{u\in B,v\in A}c(u,v)\)。而不是所谓的割掉一些边,使得 \(S\) 与 \(T\) 不连通。如果按照后者的定义来看可能会出现某个 \((i,j)\),它与 \(S,T\) 之间的边全都割掉;不过按照前者的定义来看是不会出现这种情况了。因为如果存在某个 \((i,j)\),它与 \(S,T\) 之间的边全都割掉了,我们考虑 \((i,j)\) 究竟是属于集合 \(A\) 还是集合 \(B\),如果 \((i,j)\in A\),那么它与 \(S\) 的边的权值就不会被累加到答案中;同理如果 \((i,j)\in B\),那么它与 \(T\) 的边的权值就不会被累加到答案中。故这种情况是不会出现的。
那么为什么很多人(包括我)会把割的定义误解成后者呢?因为如果按照后者的定义来理解,那最大流等于最小割的定理也是成立的;也就是说如果你割掉了一个集合 \(E'\subseteq E\) 中的边使得 \(S\) 与 \(T\) 不连通,那么 \(E'\) 中所有边容量之和的最小值就等于最大流。
证明:设 \(A\) 为割掉 \(E'\) 后 \(S\) 能到达的点集,\(B\) 为割掉 \(E'\) 后能到达 \(T\) 的点集。如果割掉 \(E'\) 后存在某个点 \(u\) 既不属于 \(A\) 也不属于 \(B\),那么把 \(u\) 归约到 \(A\) 或 \(B\) 中割的权值肯定会更小。否则,设 \(W\) 为割 \(A,B\) 的权值,显然 \(A,B\) 之间的边肯定都属于 \(E'\),否则 \(S\) 与 \(T\) 就连通了。而 \(E'\) 中可能还含有故 \(E'\text{的权值和}\leq W\)。也就是说每个 \(E'\) 都能映射到一个割 \(A,B\) 上并且 \(E'\) 的权值和不小于割 \(A,B\) 的权值。故原命题成立。
上述直接暴搜找增广路的算法由被称为 FF 算法。
由于我们每次只找增加流量是路上最小的权值,效率非常低下。网上有些题解试图简单卡 FF。
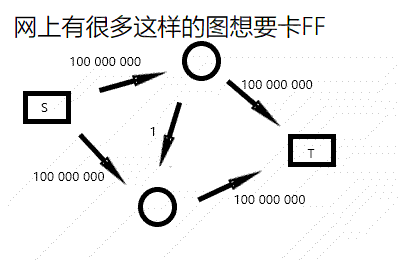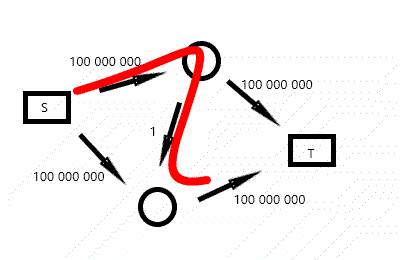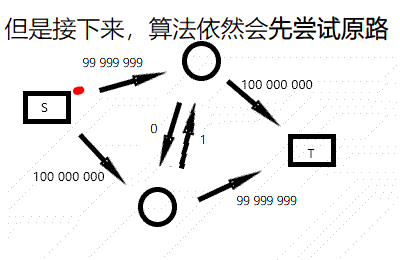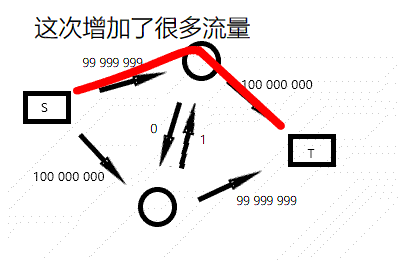
虽然这种图卡不掉 FF,但你可以看出,FF 的复杂度和流量有关,具体来说,FF 的复杂度最坏可高达 \(\mathcal O(nmf)\)(虽然异常跑不满——ycx),其中 \(f\) 为最大流大小。简直是太逊了。
考虑优化 FF,我们注意到 FF 算法中有一句”任意找一条 \(S\to T\) 的路径“。将其改为找出“\(S\to T\) 长度最短的增广路径”,就可以得到 EK(动能)算法。
加了这个小小的优化之后,算法时间复杂度会有怎样的变化呢?
你可能不太相信,可就仅仅是这个小优化,就将算法的复杂度降到了多项式级别。
证明 EK 算法复杂度为 \(\mathcal O(nm^2)\)
又一个定理证明,感觉这篇博客中要证明 inf 个定理 wdnmb
ycx 的博客真香,ycx AK IOI,永远真包含我的神%%%
首先有个引理:进行一次增广之后,源点到任意点之间的最短距离单调不降。
证明:考虑反证法,假设增广前 \(S\) 到 \(x\) 的最短距离为 \(d_x\),增广后 \(S\) 到 \(x\) 的最短距离为 \(d'_x\)。假设存在某个 \(x\) 满足 \(d'_x<d_x\)(显然 \(x\neq S\),因为 \(d'_S=d_S=0\)),并且它是增广后 \(S\) 到 \(x\) 最短路径上第一个满足 \(d'_x<d_x\) 的 \(x\)。那么我们就找出增广后 \(S\) 到 \(x\) 最短路径上的前一个点 \(y\)。那显然有 \(d'_y\geq d_y\),而又有 \(d'_x=d'_y+1\)。
下面就 \(d_x\) 与 \(d_y\) 关系分两种情况讨论:
-
\((y,x)\) 增广前的剩余流量不为 \(0\),那么根据最短路的经典不等式有 \(d_x\leq d_y+1\),结合 \(d'_x<d_x,d'_y\geq d_y,d'_x=d'_y+1\) 可得 \(d'_x<d_x\leq d_y+1\leq d'_y=d'_x-1\),即 \(d'_x<d'_x-1\),矛盾!
-
\((y,x)\) 增广前剩余流量为 \(0\),也就是说 \((y,x)\) 本来不属于 \(E\)。那肯定是它的反向边 \((x,y)\) 在增广路上。那么就要 \(d_y=d_x+1\),结合 \(d'_x<d_x,d'_y\geq d_y,d'_x=d'_y+1\) 可得 \(d'_x<d_x=d_y-1\leq d'_y-1=d'_x-2\),即 \(d'_x<d'_x-2\),矛盾!
综上,假设不成立,原命题成立。
接着考虑证明复杂度。显然一次 \(bfs\) 是 \(\mathcal O(m)\) 的,我们只需证明增广次数最多为 \(\mathcal O(nm)\) 即可。显然每次增广会有一条流量最小的边 \(e=(x,y)\),进行完此轮增广后这条边就消失了(剩余流量为 \(0\)),要让它再一次被增广需要增广它的反向边。假设有一条边 \((x,y)\) 被增广了两次,那么在两次增广中间肯定会增广一次其反向边 \((y,x)\)。根据增广的时候 \((x,y)\) 肯定在 \(S\to T\) 的最短路上,有第一次增广 \((x,y)\) 的时候 \(d_y=d_x+1\),增广其反向边的时候 \((y,x)\) 的时候 \(d'_x=d'_y+1\)。而根据「引理」有 \(d'_y\geq d_y\),于是 \(d'_x\geq d_x+2\),也就是说每次 \((x,y)\) 被重新增广时 \(d_x\) 都会增加至少 \(2\)。由于 \(S\) 到 \(x\) 的增广路最多 \(n-1\),故每条边被当作关键边增广次数至多是 \(\mathcal O(n)\) 的,故总增广次数最多为 \(\mathcal O(nm)\)。
但怎么说呢,wll 这个东西就是玄学+玄学+玄学(愈加强烈),所以这个 \(\mathcal O(nm^2)\) 还是异常跑不满。
Dinic 算法与当前弧优化
Dinic 算法
显然上述算法复杂度过高了,随随便便就能把它卡掉,在 OI 中不常用。取而代之的是下面要讲的 Dinic 算法。
在 EK 算法中我们一次只能增广一条路径,但是从 \(S\) 到 \(T\) 可能有很多很多条最短路径,如果我们一次性把它们全增广一遍会有什么变化呢?
这就是 Dinic 算法。
具体来说,在跑 Dinic 的时候,我们先一遍 \(bfs\) 求出源点到各个点的最短距离 \(d_x\),并将图分层。然后只考虑 \(d_y=d_x+1\) 的边 \((x,y)\)。我们从 \(S\) 开始携带 \(\infty\) 的流并往下递归。递归的时候,枚举当前节点的所有邻居,并尽量将手头的流发给它的邻居并继续递归下去,递归结束之后更新手头的流。如果手头没流了或访问完了所有邻居就直接返回。如果发现已经到达了汇点 \(T\) 就直接把手头的流全部送出去。
代码如下:
int hd[MAXN+5],to[MAXE+5],nxt[MAXE+5],ec=1;ll cap[MAXE+5];
void adde(int u,int v,ll f){to[++ec]=v;cap[ec]=f;nxt[ec]=hd[u];hd[u]=ec;}
/*
注意,这边有个小 trick,通常写前向星的时候习惯写 int ec=0;
但这里却是 int ec=1;
因为我们要储存反向边,我们通常加边都是两个两个一块儿加的,比如说第一个添加的边编号是 2,其反向边的编号是 3,此时我们就可以用 e^1 来表示编号为 e 的边的反向边
*/
int dep[MAXN+5],now[MAXN+5];
bool getdep(){//bfs 求出源点到所有点的最短路径
queue<int> q;memset(dep,-1,sizeof(dep));
q.push(S);dep[S]=0;
while(!q.empty()){
int x=q.front();q.pop();
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];ll z=cap[e];
if(!~dep[y]&&z){dep[y]=dep[x]+1;q.push(y);}
}
}
return (dep[T]!=-1);//如果 S 到不了 T 就说明不能增广了,直接返回当前流量
}
ll getflow(int x,ll f){//递归求单次增广送出去的流量
if(x==T) return f;//到达汇点了,直接返回手中的流量
ll ret=0;//当前送出去了多少流
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];ll z=cap[e];
if(dep[y]==dep[x]+1&&z){//在单次增广中,我们只考虑 dep[y]=dep[x]+1 的边 (x,y)
ll w=getflow(y,min(f-ret,z));//尽量送出手头的流:手头还有 f-ret 的流,这条边的剩余流量为 z,最多能流过去 min(f-ret,z) 的流量
cap[e]-=w;cap[e^1]+=w;ret+=w;//更新当前边的剩余容量及其反向边的流量
if(ret==f) return f;//如果手头的流全送完就直接返回
}
}
return ret;
}
ll dinic(){
ll ret=0;
while(getdep()) ret+=getflow(S,INF);
return ret;
}
当前弧优化
注意到每次我们有效边组成的子图一定是一个 DAG,这意味着如果我们已经访问过了一条边(即把这条边的流量耗尽了),那我们以后就不用再访问这条边了。于是我们考虑开一个数组 \(now_x\) 表示当前考虑到了哪一条弧。每次重新 bfs 就把 \(now_x\) 设为邻接表的表头。然后在 getflow 函数中,每访问一个节点 \(x\),访问到哪条边就把 \(now_x\) 设为多少。下一次再访问 \(x\) 就直接从 \(now_x\) 开始访问。
这个小优化被称为“当前弧优化”。
时间复杂度
+1 一级标题到五级标题
加了这两个优化之后,算法复杂度降到了 \(\mathcal O(n^2m)\),并且还是异常跑不满。
证明:wdnmb 又一个证明
首先可以证明增广轮数是 \(\mathcal O(n)\) 的。一次 dinic 显然等价于增广所有 \(S\) 到 \(T\) 的最短路。我们只需证明 \(S\) 到 \(T\) 的最短路单调递增即可。考虑反证法,假设增广前后 \(S\) 到 \(T\) 的最短路不变,那么增广后存在一条 \(S\to T\) 的路径,\(S\) 到路径上每个点的最短路依次为 \(0,1,2,\dots,d\)。根据证明 EK 复杂度的时候用到的定理「进行一次增广之后,源点到任意点之间的最短距离单调不降」,增广前 \(S\) 到这些点的最短路依次小于等于 \(0,1,2,\dots,d\)。而根据增广前后 \(S\) 到 \(T\) 的最短路不变,增广前 \(S\) 到 \(T\) 最短路长度应当也为 \(d\)。下面又可分为两种情况:
- 增广前这条路径上的点不存在前后两点,满足增广前 \(S\) 到前一个点的最短距离 \(\leq\) 到后一个点的最短距离 \(-2\)。这种情况下增广前 \(S\) 到这条路径上的点的最短路径只能依次为 \(0,1,2,\dots,d\)。而我们 dinic 的本质是一次性增广所有 \(S\) 到 \(T\) 的最短路,所以这样的路径一定会被增广,矛盾!
- 增广前这条路径上的点存在前后两点,满足增广前 \(S\) 到前一个点的最短距离 \(\leq\) 到后一个点的最短距离 \(-2\)。由于一轮增广只可能在最短路相邻的点之间增加 / 删除边,所以这两项之间肯定本来就有边,故 \(S\) 到前一个点的最短距离 \(\geq\) 到后一个点的最短距离 \(-1\),矛盾。
接下来证明每轮增广的复杂度是 \(\mathcal O(nm)\) 的。这个相对来说比较容易。我们考虑那些一条边都没伸出去的点,那么它对时间复杂度的贡献应为 \(S\) 到它的最短距离。这显然会使至少一条边被增广,当前弧改变。而当前弧最多改变 \(m\) 次,故一次增广的复杂度上界为 \(\mathcal O(nm)\)
两者一结合,就可以得到 dinic 的理论时间复杂度上界 \(\mathcal O(n^2m)\)
然而 dinic 算法仍旧不是最高效的求最大流的做法,还有什么 ISAP、HLPP 之类的算法能够进一步提高算法的效率。不过 dinic 算法是 OI 界中最常用的求最大流的算法,其 \(n^2m\) 的复杂度一般不会被卡,除非出题人不想要他的🐎,至于那些更高效的求最大流的算法,等我真的碰到道卡 dinic 的毒瘤妹妹题的时候再学罢。
最小费用最大流
好了终于聊完了最大流
最小费用最大流,顾名思义,就是在最大流的基础上再定义一个费用函数 \(w(x,y)(x,y\in V)\),要求在满足最大流的前提下,最小化 \(\sum\limits_{x,y\in V\&f(x,y)>0}f(x,y)\times w(x,y)\)。
那么最小费用最大流怎么求呢?很简单,在 EK 中,我们每次增广路径为 \(S\to T\) 经过的点数最少的路径。我们只需改成 \(S\to T\) 费用和最少的路径即可。由于反向边相当于退流,故原图中某条边 \(e\) 的反向边 \(\bar{e}\) 的费用为 \(e\) 的费用的相反数。注意:因为有负权边,故最短路应用 SPFA instead of Dijkstra。(其实也有用 Dijkstra 实现的最小费用最大流,可我学不动了/kk)
该算法可使用的前提条件是 \(G\) 中不存在负圈。
正确性证明
首先证明一个引理:假设有流量为 \(i\) 的流 \(f\),如果 \(f\) 是流量为 \(i\) 的流中费用最小的,就意味着 \(f\) 的残余网络中没有负圈。
假设有两个流量相同的流 \(f_1,f_2\),满足 \(f_1\) 的费用 \(<\) \(f_2\) 的费用。考虑将这两个流做差 \(\Delta f=f_1-f_2\),由于 \(f_1,f_2\) 流量相同,所以 \(\Delta f\) 一定满足:所有节点(包括 \(S\) 和 \(T\))的流入量等于流出量。也就是说 \(\Delta f\) 是由若干个圈组成的。而 \(f_1\) 的费用 \(<\) \(f_2\) 的费用,故 \(\Delta f\) 中一定存在一个负圈。也就是说,对于已知的流 \(f\),如果存在一个与 \(f\) 流量相同的流 \(f'\) 满足 \(f'-f\) 中有负圈,那么 \(f\) 一定不是所有流量与 \(f\) 相等的流中流量最大的。考虑将 \(f'-f\) 换成 \(f\) 的残量网络 \(c-f\),由于 \(f'\) 中每条边的流量 \(\leq\) 这条边的容量,故在 \(f'-f\) 中所有容量为正的边,在 \(c-f\) 中的容量依然为正,也就是说 \(f'-f\) 中的负圈在 \(c-f\) 中依然存在。故若流 \(f\) 的残余网络中有负圈,那么 \(f\) 一定不是是流量为 \(i\) 的流中费用最小。故原命题成立。
有了这个引理之后,就可以用归纳法证明了。设 \(f_i\) 为流量为 \(i\) 的流中费用最小的流。我们找出 \(f_i\) 的残量网络中 \(S\) 到 \(T\) 的总费用最小的路径,并通过增广 \(P\) 转移到 \(f_{i+1}\)。假设 \(f_{i+1}\) 不是流量最小的流,那么设 \(f'_{i+1}\) 为流量为 \(i+1\) 的费用比 \(f_{i+1}\) 更小的流。考虑作差,令 \(\Delta f=f'_{i+1}-f_i\),显然 \(\Delta f\) 中源点的流出量为 \(1\),汇点的流入量为 \(1\),其余点都满足流入量等于流出量。即 \(\Delta f\) 是由一条 \(S\to T\) 的路径和若干个圈组成的。由于 \(f_{i+1}-f_i\) 是 \(S\to T\) 的最短路径,故 \(\Delta f\) 中路径部分的费用肯定大于等于 \(f_{i+1}-f_i\) 的费用。而根据 \(f'_{i+1}\) 的费用小于 \(f_{i+1}\) 可知 \(\Delta f\) 的费用小于 \(f_{i+1}-f_i\) 的费用。故 \(\Delta f\) 肯定存在负圈,也就是说 \(f_i\) 肯定存在负圈,根据「引理」可知 \(f_i\) 不是流量为 \(i\) 的流中费用最小的流,这与 \(f_i\) 是流量为 \(i\) 的流中费用最小的流矛盾!故由 \(f_i\) 增广得到的 \(f_{i+1}\) 为流量为 \(i+1\) 的流中费用最小的流。而由于 \(G\) 中不含负圈,故 \(f_0\) 等于空流。根据数学归纳法可知这样求最小费用最大流是正确的。
上述证明过程同时也可以证明 EK 求最小费用最大流的可实现性:任意时刻图中都不含负环,故可用 SPFA。
时间复杂度
EK 求最小费用最大流的时间复杂度上界为 \(\mathcal O(nmf)\),其中 \(f\) 为最大流量。这个很好理解:最多增广 \(f\) 次,每次 SPFA 复杂度为 \(\mathcal O(nm)\)。
但还是那句话,EK 求最小费用最大流的算法是 OI 界中最常用的求最小费用最大流的算法,即便它的理论复杂度上界与流量有关,一般也没有人卡,除非出题人不想要他的🐎。
总之,「最大流不卡 Dinic,费用流不卡 EK」是完整的业界公约(
模板题代码
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=5e3;
const int MAXM=1e5;
const int INF=0x3f3f3f3f;
int n,m,S,T;
int hd[MAXN+5],to[MAXM+5],nxt[MAXM+5],cst[MAXM+5],cap[MAXM+5],ec=1;
void adde(int u,int v,int f,int c){to[++ec]=v;cst[ec]=c;cap[ec]=f;nxt[ec]=hd[u];hd[u]=ec;}
int dis[MAXN+5],flw[MAXN+5],pre[MAXN+5],lste[MAXN+5];
bool inq[MAXN+5];
bool getdis(){//SPFA求源点到汇点最短距离
memset(dis,63,sizeof(dis));memset(flw,63,sizeof(flw));//记得初始化
queue<int> q;dis[S]=0;flw[S]=INF;q.push(S);inq[S]=1;
while(!q.empty()){
int x=q.front();q.pop();inq[x]=0;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e],z=cap[e],w=cst[e];
if(dis[y]>dis[x]+w&&z){
dis[y]=dis[x]+w;flw[y]=min(flw[x],z);
pre[y]=x;lste[y]=e;//pre[i]表示i上一个点的编号,lste[i]表示i上一条边的编号
if(!inq[y]){inq[y]=1;q.push(y);}
}
}
} return dis[T]<INF;
}
pii mcmf(){
int mxfl=0,mncst=0;
while(getdis()){
mxfl+=flw[T];mncst+=dis[T]*flw[T];
for(int i=T;i!=S;i=pre[i]){
cap[lste[i]]-=flw[T];cap[lste[i]^1]+=flw[T];
}
} return mp(mxfl,mncst);
}
int main(){
scanf("%d%d%d%d",&n,&m,&S,&T);
for(int i=1;i<=m;i++){
int u,v,f,c;scanf("%d%d%d%d",&u,&v,&f,&c);
adde(u,v,f,c);adde(v,u,0,-c);//建正边和反边
} pii ans=mcmf();printf("%d %d\n",ans.fi,ans.se);
return 0;
}
一些模型
二分图
u1s1 网络流与二分图有很大的联系。
一个图 \(G=(V,E)\) 是二分图当且仅当存在两个点集 \(A,B\) 满足 \(A\cup B=V,A\cap B=\empty\),并且 \(A\) 中、\(B\) 中任意两点之间没有边相连。此时我们称 \(A\) 为二分图的左部,\(B\) 为二分图的右部。
一个图 \(G\) 是二分图的充分必要条件是它没有奇数环。
怎样判定二分图就不用多说了吧,对于每个连通块黑白染色,如果存在某条边端点颜色相同那就不是二分图。
二分图最大匹配
一个匹配是一个边集 \(E'\subseteq E\) 满足 \(E'\) 中任意两条边没有公共点。
定义一个匹配 \(E'\) 的大小为 \(|E'|\),一张图的最大匹配即为其大小最大的匹配。
二分图最大匹配的求法
对于左部的每个点 \(u\),连一条从源点到 \(u\) 的边,容量为 \(1\),表示 \(u\) 最多与一条边匹配。
对于右部的每个点 \(u\),同理连一条从 \(u\) 到汇点的边,容量为 \(1\)。
对于每条边 \(e=(u,v)\),连一条从 \(u\) 到 \(v\) 的边,容量为 \(1\),表示每条边最多匹配一次。
然后跑二分图最大匹配即可。时间复杂度 \(\mathcal O(m\sqrt{n})\)。
btw 还有一个匈牙利算法是专门干这事的,时间复杂度 \(\mathcal O(nm)\),劣于 dinic。
完备匹配
对于一张左部和右部点数都为 \(n\) 的二分图,如果其最大匹配的大小为 \(n\),那么我们就称其为这张二分图的完备匹配。
多重匹配
相当于扩展了二分图匹配的定义:本来的定义等价于每个点最多只能和一条匹配中的边关联,现改为对于点 \(x\) 最多与匹配中 \(lim_x\) 条边关联。
也很弱智,只需把每个点与源/汇点之间的边的容量(本来是 \(1\))改为 \(lim_x\) 就行了,表示这个点最多与 \(lim_x\) 条边关联,然后还是跑最大流就行了。
二分图带权匹配
带权匹配,顾名思义对于每条边定义了一个权值 \(w(x,y)\)。
一般我们遇到的二分图带权匹配都是带权最大匹配,即在满足匹配的边数最大的情况下让匹配的这些边的权值和最大。
这玩意儿实际上也异常容易:对于原来二分图左部与右部之间的边 \((u,v)\),加个费用 \(w(u,v)\)。由于要在流量最大的情况下让费用最大,故跑一遍最大费用最大流就行了。
你可能会有疑问,什么是最大费用最大流啊,我只学过最小费用最大流。
事实上只需做一个弱智的转化就行了,将每条边取个相反数,跑出来的费用就是最大费用的相反数。
最后检查一下会不会出现负环,由于我们本身建图就不会出现环,所以这样求是没问题的。
时间复杂度 \(\mathcal O(nmf)=\mathcal O(n^2m)\),据说有个 KM 算法是专门干这个的,复杂度 \(n^3\),但据说该算法局限性较大,并且一般费用流也不会被卡(毕竟有「最大流不卡 Dinic,费用流不卡 EK」的业界公约),就没学了。
二分图的边覆盖、点覆盖、独立集
对于任意一张图 \(G\),给出下面四个定义:
- 边覆盖:\(G\) 的一个边覆盖是一个边集 \(E'\subseteq E\) 满足任意 \(u\in V\) 都存在一条边 \(e\in E'\) 满足 \(u\) 是 \(e\) 的一个端点,即每个点至少被 \(E'\) 一条边关联。
- 匹配:\(G\) 的一个边覆盖是一个边集 \(E'\subseteq E\) 满足 \(E'\) 中任意两条边之间都没有公共点,即每个点至多被 \(E'\) 一条边关联。
- 点覆盖:\(G\) 的一个点覆盖是一个点集 \(V\subseteq E\) 满足对于每条边 \(e=(u,v)\),\(u,v\) 中至少有一个属于 \(V\),即每条边至少与 \(V\) 中一个点关联。
- 独立集:\(G\) 的一个点覆盖是一个点集 \(V\subseteq E\) 满足对于每条边 \(e=(u,v)\),\(u,v\) 不全属于 \(V\),即每条边至多与 \(V\) 中一个点关联。
根据上面的定义,我们不难发现边覆盖与匹配是一组的,点覆盖与独立集是一组的。事实上,对于任意图 \(G=(V,E)\)(注:本节标题为”二分图的边覆盖、点覆盖、独立集“,是因为求任意图的最大匹配是 NPC 问题,所以我们一般探讨的都是二分图的匹配、边覆盖、点覆盖、独立集,但是下面两个定理对任意图(第一个定理要求不含孤立点)都是成立的),有:
- 如果 \(G\) 中不含孤立点(否则就不存在边覆盖),那么最小边覆盖 \(+\) 最大匹配 \(=|V|\)。证明:对于某个边集 \(E'\),我们记 \(c\) 为与 \(E'\) 关联的点的个数。我们先构造出 \(G\) 的最大匹配 \(E'\),显然,对于 \(E'\) 中每条边都会对 \(c\) 产生 \(2\) 的贡献,即此时 \(c=2|E'|\),而由于 \(E'\) 是该图的最大匹配,所以以后加进来的边最多对 \(c\) 产生 \(1\) 的贡献。而我们希望 \(c\) 达到 \(n\),故以后最少要加进来 \(|V'|-2|E'|\) 条边。故最小边覆盖的大小应为 \(|E'|+|V|-2|E'|=|V|-|E'|\),得证。
- \(G\) 的最小点覆盖 \(+\) 最大独立集 \(=|V|\)。证明:对于 \(G\) 的某个独立集 \(V'\),显然每条边最多一个端点属于 \(V'\)。设 \(V''=V-V'\),根据每条边最多一个端点属于 \(V'\) 可得每条边最少一个端点属于 \(V''\)。反之亦然,故 \(G\) 的独立集与 \(G\) 的点覆盖存在一一对应,即双射关系。并且满足双射关系的两个集合大小之和为 \(|V|\)。故最小点覆盖 \(+\) 最大独立集 \(=|V|\)。
故最大匹配与最小边覆盖,最大独立集与最小点覆盖,这两组当中知道一个就能顺带着求出另一个。
那么我们不禁要问一问:二分图的最大匹配与最小点覆盖有什么关系呢?
还真有,对于一张二分图,其最大匹配就等于最小点覆盖。
证明:首先最小点覆盖肯定大于等于最大匹配 \(|E'|\),因为假设最小点覆盖小于 \(|E'|\),那么根据抽屉原理,\(E'\) 中至少有一条边两个端点都没被覆盖,不符合点覆盖的定义,矛盾。
其次,我们要证明大小为 \(|E'|\) 的点覆盖是存在的。考虑令 \(V'=\text{残余网络上左部中源点能到达的点+右部中源点不能到达的点}\),下证 \(V'\) 是原图一个点覆盖。
我们定义一个点 \(u\) 为”匹配点“,当且仅当存在某条边 \(e\in E'\),并且 \(u\) 为 \(e\) 的一个端点,反之则 \(u\) 为”非匹配点“。
首先我们有所有非匹配点都不属于 \(V'\),因为:
- 对于左部的非匹配点 \(u\),由于它没有被匹配,它与源点之间的边的剩余容量应为 \(1\),故 \(u\) 可以从源点到达。
- 对于右部的非匹配点 \(u\)。如果它能从源点到达,那么肯定存在 \(S\to u\) 的路径,而由于它没有被匹配,它与汇点之间的边的剩余容量应为 \(1\),也就存在 \(S\to T\) 的路径。那么原图中应还有增广路,不符合”一张图求完最大流的残余网络上不含增广路“,矛盾,假设不成立。故 \(u\) 不能从源点到达。
其次有对于任意一对匹配的节点 \((u,v)\),要么 \(u\in V'\),要么 \(v\in V'\)。因为由于 \((u,v)\) 匹配,\(S\to u\) 的边的剩余流量为 \(0\),也就是说 \(u\) 只能通过反向边到达。而所有与 \(u\) 相连的右部节点中,只有 \(u\to v\) 的流量为 \(1\),也就是说 \(u\) 只能从 \(v\) 到达。故如果 \(v\) 可以从 \(S\) 到达,那 \(u\) 也可以。反过来,如果 \(u\) 可以从 \(S\) 到达,由于 \(u\to v\) 的流量为 \(1\),\(u\) 可以到达 \(v\),也就是说如果 \(u\) 可以从 \(S\) 到达,那 \(v\) 也可以。故 \((u,v)\) 要么都能从 \(S\) 到达,要么都不能,故要么 \(u\in V'\),要么 \(v\in V'\)。也就是说 \(|V'|=|E'|\)。
最后要证明 \(V'\) 能覆盖 \(E\) 中所有边 \((u,v)\)(\(u\) 在左部 \(v\) 在右部)。分两种情况:
- 边 \((u,v)\) 为匹配边,那这条边一定会被覆盖——因为恰好一个端点被取走。
- 边 \((u,v)\) 不是匹配边。考虑反证法,若 \(u,v\) 都不能被覆盖,那 \(u\) 能从 \(S\) 到达,而 \(v\) 不能。而因为 \((u,v)\) 不是匹配边,故边 \((u,v)\) 的剩余流量为 \(1\),也就是说如果 \(u\) 能从 \(S\) 到达,那 \(v\) 也能。矛盾!故 \(u,v\) 中至少有一个被覆盖。
\(\therefore\) 原命题成立。
也就是说,对于二分图,我们只需求出其最大匹配就能直接求出另外三个了。
团
对于无向图 \(G=(V,E)\),如果点集 \(V'\subseteq V\),并且 \(V'\) 中任意两点都有边相连,那么我们就称 \(V'\) 为 \(G\) 的一个团。
有一个显然的结论就是 \(V'\) 是一个团当且仅当 \(V'\) 在 \(G\) 的补图中是一个独立集。
故 \(G\) 的最大团等于 \(G\) 的补图的最大独立集。如果补图是二分图就直接拿 \(|V|\) 减去补图的最大匹配即可。
Hall 定理
具体可见 题解 CF338E Optimize!,以下内容都是从那篇题解里直接搬过来的。
Hall 定理说的是这样一件事,对于二分图 \(G=(V_1,V_2,E)\),定义函数 \(f(V)(V\in V_1)\) 为与点集 \(V\) 中的点相连的点的(右部点)集合。那么二部图 \(G\) 有完美匹配的充要条件是 \(\forall V\subseteq V_1,|f(V)|\geq |V|\)
必要性:这个就比较显然了吧。。。记对于节点 \(u\),记 \(mch(u)\) 为与 \(u\) 匹配的节点。那么我们构造集合 \(V'=\{v|v=mch(u),u\in V\}\),那么 \(|V'|=|V|\),而根据 \(V'\) 的构造方式可知 \(\forall v\in V'\) 至少存在一个 \(u\in V\) 满足 \(u,v\) 间有边,故 \(V'\subseteq f(V)\),于是有 \(|V|=|V'|\leq f(V)\),得证。
充分性:这个就没那么显然了。考虑反证法,假设二分图 \(G\) 不存在完美匹配但满足 Hall 定理。那么我们构造出 \(G\) 的一种最大匹配,其中必存在某个非匹配点,假设其为 \(A\)。根据 Hall 定理 \(A\) 必定与另一边某个点相连,设其为 \(B\)。而 \(B\) 必须为匹配点,否则 \(A,B\) 就能形成新的匹配,不满足最大匹配的条件了,设 \(C\) 为与 \(B\) 相匹配的点。再对集合 \(\{A,C\}\) 使用 Hall 定理可知,\(\{A,C\}\) 除 \(B\) 外必与其它某个点相连,设其为 \(D\)。\(D\) 也必须为匹配点,否则根据之前的证明过程可知它不能与 \(A\) 相连,否则 \(A,D\) 能形成新的匹配,故它只能与 \(C\) 相连,而若它与 \(C\) 相连,那么将匹配边 \((B,C)\) 换为 \((A,B),(C,D)\) 可让匹配个数多 \(1\),不满足最大匹配的条件,故 \(D\) 一定与某个点 \(E\) 匹配。再对集合 \(\{A,C,E\}\) 使用 Hall 定理可得还存在某个点 \(F\) 与这三个点都相连且为匹配点。如此一直进行下去可进行无限轮,而点集的大小是有限的,矛盾!
Dilworth 定理
我为此专门写了篇 blog
最大权闭合子图
最大权闭合子图是指这样一类问题:假设我们有一张有向图 \(G=(V,E)\),现在要从中选出一个点集 \(V'\subseteq V\),满足对于任意一条边 \((x,y)\),若 \(x\in V'\),那么 \(y\in V'\)。现在给每个点赋上一个点权 \(w_i\),其中 \(w_i\) 可正可负。最大化 \(\sum\limits_{x\in V'}w_x\)。
首先考虑最理想的情况,那就是所有 \(w_i>0\) 的点都被选择,所有 \(w_i<0\) 的点都不被选择,这样选择的点的权值和肯定是所有点集中最大的。但是这样未必满足“最大权闭合子图”的限制,故我们要对其进行调整。
具体来说,我们可以用最小割来解决这个问题。对于 \(w_i>0\) 的点连一条从 \(S\) 到 \(i\),容量为 \(w_i\) 的边,若割掉这条边则表明不选择 \(i\),否则表明选择 \(i\);对于 \(w_i<0\) 的点连一条从 \(i\) 到 \(T\),容量为 \(-w_i\) 的边,若割掉这条边则表明选择 \(i\),否则表明不选择 \(i\)。
接下来我们考虑这个“最大权闭合子图”的限制怎么在图中体现。对于原图中的边 \((u,v)\),我们连一条从 \(u\) 到 \(v\),容量为 INF(在最小割中,容量为 INF 意味着割不掉)的边。然后求最小割即最大流。
为什么呢?假设有一条 \(S\) 到 \(T\) 的路径 \(S\to v_1\to v_2\to v_3\to\dots\to v_k\to T\),\(S\to v_1\) 有边相连说明 \(v_1\in V'\),而 \((v_1,v_2)\in E,v_1\in V'\) 可以推出 \(v_2\in V'\),以此类推,最后可以得到 \(v_k\in V'\)。而 \(v_k\) 与 \(T\) 之间的边没被割断说明 \(v_k\) 不属于 \(V'\),矛盾!不符合题意。
故如果图中存在 \(S\) 到 \(T\) 的路径就意味着出现了不合法的情况。跑最小割即可解决这个问题。
一些建模技巧:
-
多源多汇的网络流:源点有多个,汇点有多个,流可以从任意一个源流出,最终可以流向任意一个汇,总流量等于所有源流出的总流量,也等于所有汇流入的总流量。
解法:新建一个超级源点 \(S\) 和一个超级源点 \(T\),然后从超级源点向每个源点连边,容量为 INF;从每个汇点向超级汇点连边,容量为 INF。跑最大流即可。
-
节点有容量限制的网络流:每个节点有一个流量限制,最多只能有 \(c_u\) 的流量经过点 \(u\)。
解法:拆点,将每个点拆为 \(in_u\) 和 \(out_u\),并在 \(in_u\) 与 \(out_u\) 之间连边,容量为 \(c_u\);然后对于原图中的每条容量为 \(f\) 的边 \((u,v)\),连一条从 \(out_u\) 到 \(in_v\) 的边,容量为 \(f\)。然后跑最大流即可。
-
费用与流量的平方成正比的费用流:容量 \(c\) 均为整数,且每条弧有一个费用系数 \(a\),该弧流量为 \(x\) 时费用为 \(ax^2\),求最小费用最大流。
解法:差分建图,将这条边拆成若干条边,容量均为 \(1\),费用依次为 \(a,3a,5a,\dots\);当费用与流量的三次方成正比的时候也同理。
-
带时间轴的问题:在网络流中我们常会碰到这样一个问题:初始你在某个状态,在 \(t\) 时刻你可以从某个状态到达 \(t+1\) 时刻的下一个状态,然后还有个什么流量限制之类的。
解法:这种问题一般可以用分层建图的方式解决,即将每个 \((\text{时间},\text{状态})\),看作一个节点。如果 \(t\) 时刻你可以从某个状态 \(u\) 到达 \(t+1\) 时刻的下一个状态 \(v\),那么就从 \((t,u)\) 连向 \((t+1,v)\),然后根据情况跑最大流/费用流。
-
最小割的应用:形如“有 \(n\) 个点,每个点有两种决策,如果选择第一种方案那可以获得 \(a_i\) 分,选择第二种方案可以获得 \(b_i\) 分;有 \(m\) 个二元组 \((x,y)\) 表示 \(x,y\) 不是同一种方案/如果 \(x,y\) 是同一种方案那可以得到 \(c\) 分,求得分的最大值”之类的问题。
解法:这种题目使用最小割解决,由于只有两种决策,我们可以连一条从 \(S\) 到 \(i\),容量为 \(a_i\) 的边,割掉这条边表示不选第一种方案,即选择第二种方案;再连一条从 \(i\) 到 \(T\),容量为 \(b_i\) 的边,割掉这条边表示不选第二种方案,即选择第一种方案。然后对于每个二元组 \((x,y)\) 在 \(x,y\) 之间连容量为 INF 的边,表示这条边割不掉。大体思路就是如果存在 \(S\to T\) 的路径就意味着方案不合法,故通过最大流等于最小割定理求出最大流,也就求出最小割了。具体应用见题目罢。
有上下界的网络流
有上下界的网络流,顾名思义,就是对每条边又定义了个函数 \(b(x,y)(x\in V,y\in V)\),要求 \(b(x,y)\leq f(x,y)\leq c(x,y)\)。
有上下界网络流可分为无源汇上下界可行流、有源汇上下界可行流、有源汇上下界最大/小流三种。加上这三种模型分别带费用的版本,一共是六种有上下界网络流。下面对其一一作出介绍。
无源汇上下界可行流
刚学上下界网络流的萌新可能会问,在本博客一开始不是明确规定说一个网络必须要有源和汇吗?为什么还会有无源汇的网络流呢?
事实上,这玩意儿相当于扩展了网络的定义。无源汇就要求每个点都要满足流量守恒。这样就没有了总流量的概念,就只有可行流了。
无源汇上下界可行流,就是要构造出流函数 \(f(x,y)\),使得 \(b(x,y)\leq f(x,y)\leq c(x,y)\),并且 \(\forall u\in V,\sum\limits_{(v,u)\in E}f(v,u)=\sum\limits_{(u,v)\in E}f(u,v)\)。
考虑怎样求无源汇上下界可行流。由于 \(b(x,y)\leq f(x,y)\),所以我们不妨给每条边先流上 \(b(x,y)\) 的流量。令 \(f'(x,y)=f(x,y)-b(x,y)\),那么 \(0\leq f'(x,y)\leq c(x,y)-b(x,y)\),就转化为无下界的情况了。
但显然这样不一定满足流量守恒。令 \(in_u=\sum\limits_{(v,u)\in E}b(v,u),out_u=\sum\limits_{(u,v)\in E}b(u,v)\),也就是在每条边都流上 \(b(x,y)\) 的流量的情况下,每个点的流入量和流出量。如果 \(in_u>out_u\),则表明 \(u\) 还需流出 \(in_u-out_u\) 的流量;否则表明 \(u\) 还需流入 \(out_u-in_u\) 的流量。
考虑借鉴「负载平衡问题」的套路,对于每个 \(in_u>out_u\) 的点,连一条从 \(S\) 到 \(u\),容量为 \(in_u-out_u\) 的边,表示 \(u\) 可以给外界提供 \(in_u-out_u\) 的流量;对于每个 \(in_u<out_u\) 的点,连一条从 \(u\) 到 \(T\),容量为 \(out_u-in_u\) 的边,表示 \(u\) 需要 \(out_u-in_u\) 的流量。然后对于 \((u,v)\in E\),连一条从 \(u\) 到 \(v\),容量为 \(c(u,v)-b(u,v)\) 的边。然后跑最大流,看看是否满流即可。如果没满则无可行流,否则存在可行流,每条边的实际流量为这条边在建出的图中的实际流量 \(+b(x,y)\)。
为什么?考虑一条 \(S\to T\) 的增广路 \(S\to v_1\to v_2\to\dots\to v_k\to T\),假设它增广了 \(f\) 的流量,那么其实质是将 \(v_1\) 的 \(f\) 个单位的流量转移到 \(v_k\)。也就是说对于每个 \(in_u>out_u\) 的点,其与 \(S\) 之间的边的实际流量就是它转移出去了多少的流量,故当且仅当其与 \(S\) 之间的边的满流的时候才有 \(\sum\limits_{(v,u)\in E}f(v,u)=\sum\limits_{(u,v)\in E}f(u,v)\)。同理可得\(in_u<out_u\) 的点。而显然所有与 \(S\) 相连的边的容量之和等于所有与 \(T\) 相连的边的容量之和。故如果最大流没有满流,就意味着肯定存在某个点与源点/汇点之间的边没有满流,也就不符合题意了。如果最大流满流了,就意味着所有点与源点/汇点之间的边都满了,符合题意。
最后考虑实现。事实上你并不用把 \(in_u,out_u\) 都求出来。对于一条边 \((u,v)\),由于我们事先给它流了 \(b(u,v)\) 的流量,\(in_v\) 会增加 \(b(x,y)\),于是我们可以直接连一条从 \(S\) 到 \(v\),容量为 \(b(u,v)\) 的边;同理 \(out_u\) 会增加 \(b(x,y)\),故我们可以也连一条从 \(u\) 到 \(T\),容量为 \(b(u,v)\) 的边。这样的建图方式与上文中所说的是等价的。
模板题代码:
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=200+2;
const int MAXM=1e5;
const int INF=0x3f3f3f3f;
int n,m,S=201,T=202;
int hd[MAXN+5],to[MAXM+5],nxt[MAXM+5],cap[MAXM+5],ec=1;
void adde(int u,int v,int f){
to[++ec]=v;cap[ec]=f;nxt[ec]=hd[u];hd[u]=ec;
to[++ec]=u;cap[ec]=0;nxt[ec]=hd[v];hd[v]=ec;
}
int dep[MAXN+5],now[MAXN+5];
bool getdep(){
memset(dep,-1,sizeof(dep));dep[S]=0;
queue<int> q;q.push(S);now[S]=hd[S];
while(!q.empty()){
int x=q.front();q.pop();
for(int e=hd[x];e;e=nxt[e]){
int y=to[e],z=cap[e];
if(!~dep[y]&&z){dep[y]=dep[x]+1;now[y]=hd[y];q.push(y);}
}
} return dep[T]!=-1;
}
int getflow(int x,int f){
if(x==T) return f;int ret=0;
for(int &e=now[x];e;e=nxt[e]){
int y=to[e],z=cap[e];
if(dep[y]==dep[x]+1&&z){
int w=getflow(y,min(z,f-ret));
ret+=w;cap[e]-=w;cap[e^1]+=w;
if(ret==f) return ret;
}
} return ret;
}
int dinic(){
int ret=0;
while(getdep()) ret+=getflow(S,INF);
return ret;
}
int main(){
scanf("%d%d",&n,&m);int sum=0;
for(int i=1;i<=m;i++){
int u,v,b,c;scanf("%d%d%d%d",&u,&v,&b,&c);
adde(u,v,c-b);adde(S,v,b);adde(u,T,b);sum+=b;//sum表示所有与S/T相邻的边的容量和
} int mxfl=dinic();if(mxfl!=sum) return puts("NO"),0;//如果没有满流就没有可行流
puts("YES");
for(int i=3;i<=ec;i+=6) printf("%d\n",cap[i]+cap[i+2]);
return 0;
}
加上费用的版本也同理。还是先给每条边流 \(b(x,y)\) 的流量,费用加上 \(b(x,y)\times w(x,y)\)。按照上面的方式建出图来,最后跑个最小/大费用最大流即可。
有源汇上下界可行流
其实异常简单。。。
有源汇的情况实际上是除了 \(S,T\) 之外其他点都满足流量守恒,而 \(S\) 的流出量等于 \(T\) 的流入量。
考虑怎样将有源汇的情况转化为无源汇的情况。只需在 \(T\) 与 \(S\) 之间连一条容量为 INF 的边,把 \(T\) 的流量转移到 \(S\) 即可,这样 \(S\) 和 \(T\) 也满足流量守恒了。
再跑无源汇上下界网络流就可以得到一组可行流了,其流量为 \(T\) 与 \(S\) 之间边的流量。
有源汇上下界最大/小流
首先,先找出任意一个可行流——怎么找就不用多说了吧,前面已经讲的很清楚了
这样除了 \(S\) 和 \(T\) 其它点都满足流量守恒和容量下限了,此时只需把 \(S\) 与 \(T\) 之间的边删去,再在残余网络上跑一遍 \(S\) 到 \(T\) 的最大流了。别忘了加上原来 \(T\) 与 \(S\) 之间边的流量。
那最小流怎么求呢?其实也很 easy:考虑从 \(T\) 向 \(S\) 跑增广路其实等价于退流,于是跑一遍 \(T\) 到 \(S\) 的最大流,并用原来的流量减去这个最大流就行了。
带负圈的费用流
这个方法就多了,有一种方法被称之为“消圈方法”,但复杂度和实现难度都较大。这里提供一种较为巧妙的方法:先假设所有负权边都满流,此时它的反向边流量应为 \(c(x,y)\),也就是说连边 \((x,y,c(x,y),-w(x,y))\),这样就不出现负权边了。但这样不一定满足流量守恒,此时我们可以借鉴「有源汇上下界最大/小流」的套路,跑一遍有源汇最小费用最大流即可。
最小费用可行流
这时候没有所求流是最大流的限制条件了,只要求在所有可行流中费用最小的(最大也同理)。
首先注意到如果没有负权边那显然空流就满足条件。如果存在负权边,那就按照「带负圈的费用流」的套路,假设所有负权边都满流,然后调整即可。
总结
什么?怎么这就结束了?你说还有什么最小割树之类的?那玩意儿大概不怎么用得到罢。。。
引用某老师的话:“xxx就是一个框,什么都可以往里装“
这句话同样适用于网络流”网络流就是一个框,什么都可以往里装“
网络流,总结起来,关键就是要理解每个模型(二分图、拆点最大流、费用流、最小割、上下界网络流等等)的求解方法以及适用场景。一般网络流题做不出来要么是看不出来是网络流,要么是看出来是网络流却不会建模。而这就需要通过不断刷题来加深感觉。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号