计算几何基础
zszz,tzc 对计算几何一窍不通,所以他现在终于开始 Van 计算几何辣(
一些基础芝士
-
点、直线、线段:这些就不用多说了吧,小学就知道了。在本文中,用大写字母 \(ABC\) 表示点,用小写字母 \(l,a\) 等表示直线/线段。注意,在计算几何中,由于有可能出现斜率为
nan的情况,因此通常不用 \(y=kx+b\) 的形式表示直线,而采用两点式,即直线上两个点的形式表示直线,也有极少数情况使用 \(Ax+By+C=0\) 的一般式。 -
向量:可以看作带方向的线段,用 \(\vec{AB}\) 表示。与有向线段的区别在于我们不关心向量的具体位置,只关心它的方向和长度。由于向量的位置不重要,因此我们完全可以把向量的一个端点移到原点出,这样另一个点的位置就唯一确定了这个向量,因此向量和点一样可以用坐标的形式表示。(当然如果真要区分向量&点,可以使用齐次坐标表示法,即在后面增加个第三维 \(0/1\) 加以区分,有兴趣的同学可以好好研究下 THUSC2021 day2,这里就不赘述了)
-
向量的运算
- 加减法:根据平行四边形法则,两个向量加/减就直接对应坐标加/减即可。
- 数乘向量:对于向量 \(\vec{u}=(x,y)\),\(\lambda\vec{u}=(\lambda x,\lambda y)\)
- 向量的点积:对于向量 \(\vec{u}=(x_1,y_1),\vec{v}=(x_2,y_2)\),\(\vec{u}·\vec{v}=x_1x_2+y_1y_2\)
- 向量的叉积:对于向量 \(\vec{u}=(x_1,y_1),\vec{v}=(x_2,y_2)\),\(\vec{u}\times\vec{v}=x_1y_2-x_2y_1\)(顺带提一句,向量叉积是有方向的,垂直于 \(\vec{u},\vec{v}\) 所在的平面,不过似乎 OI 里面用不到(?Fog))
前两个运算都比较好理解,难点是后两个,尤其是向量叉积,在计算几何中非常常用。
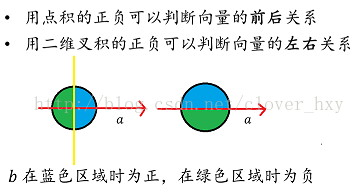
向量叉积的几何意义:\(\vec{u}\times\vec{v}\) 的绝对值为以 \(\vec{u},\vec{v}\) 为两边的平行四边形的面积,即 \(|\vec{u}\times\vec{v}|=|\vec{u}|·|\vec{v}|·\sin<\vec{u},\vec{v}>\),如果 \(\vec{v}\) 在 \(\vec{u}\) 的逆(upd. 2022.7.24)时针方向则 \(\vec{u}\times\vec{v}\) 为正,如果 \(\vec{u},\vec{v}\) 夹角为 \(0\) 或 \(\pi\) 则 \(\vec{u}\times\vec{v}=0\),如果 \(\vec{v}\) 在 \(\vec{u}\) 的顺(upd. 2022.7.24)时针方向则 \(\vec{u}\times\vec{v}\) 为负,OI 里常用向量叉积的符号判断两个向量的位置关系。
向量点积的几何意义:\(\vec{u}·\vec{v}\) 为 \(\vec{u}\) 的长度乘以 \(\vec{v}\) 在 \(\vec{u}\) 上投影的长度,如果 \(\vec{u}\) 在 \(\vec{v}\) 投影的位置在 \(\vec{u}\) 的反向延长线上则需取个相反数,即 \(\vec{u}·\vec{v}=|\vec{u}|·|\vec{v}|·\cos<\vec{u},\vec{v}>\)
下图较为清楚的解释了向量叉积、点积的符号与位置的关系(左边是点积,右边是叉积):
-
向量的模长、幅角:
与复数类似,学过复数的应该都比较好理解罢:
- 模长:对于 \(\vec{u}=(x,y)\),\(|\vec{u}|=\sqrt{x^2+y^2}\)。
- 幅角:对于 \(\vec{u}=(x,y)\),\(\vec{u}\) 的幅角为以 \(x\) 轴正半轴为始边,\(\vec{u}\) 为终边的角的大小,可以用 \(\arg\vec{u}\) 表示,C++ 里可以用函数
atan2(y,x)实现,范围在 \([-\pi,\pi]\) 中,极角排序(这个下面会讲)时使用起来很方便(PS:这个函数有两个缺陷,一是常数比较大,调用 \(5\times 10^7\) 次这个函数大约要 2s,二是精度容易爆,所以用的时候要稍加注意)
一些常用函数及调用方法
首先是一些宏和类,sgn 表示是正数还是负数还是 \(0\),其中经过了精度处理,point 是一个表示点的结构体
const double EPS=1e-6;
int sgn(double x){return (x>EPS)?1:((x>-EPS)?0:-1);}
struct point{
double x,y;
point(double _x=0,double _y=0):x(_x),y(_y){}
point operator +(const point &rhs) const{return point(x+rhs.x,y+rhs.y);}
point operator -(const point &rhs) const{return point(x-rhs.x,y-rhs.y);}
point operator *(const double &rhs) const{return point(x*rhs,y*rhs);}
point operator /(const double &rhs) const{return point(x/rhs,y/rhs);}
double operator |(const point &rhs) const{return x*rhs.y-y*rhs.x;}
double operator ^(const point &rhs) const{return x*rhs.x+y*rhs.y;}
double operator ~() const{return sqrt(x*x+y*y);}
double operator !() const{return atan2(y,x);}
}
判断两条线段是否有交点
u1s1 在没有学过向量叉积之前,实现这个函数需要写一堆分类讨论,难以推广,现在学了向量叉积了就理解许多了。
首先我们考虑对于一条直线 \(l\) 上的两点 \(A,B\) 以及 \(l\) 所在平面内一点 \(P\),\(\vec{PA}\times\vec{PB}\) 的符号所表示的意义,简单画个图即可发现,如果 \(P\) 在向量 \(\vec{AB}\) 所示方向的左侧,那么从 \(\vec{PA}\) 旋转到 \(\vec{PB}\) 需要顺时针旋转,故 \(\vec{PA}\times\vec{PB}>0\),同理如果 \(P\) 在向量 \(\vec{AB}\) 所示方向的右侧,那么从 \(\vec{PA}\) 旋转到 \(\vec{PB}\) 需要逆时针旋转,故 \(\vec{PA}\times\vec{PB}<0\)。一言以蔽之:\(\vec{PA}\times\vec{PB}\) 的符号暗示了点 \(P\) 在直线 \(l\) 的哪一侧。
知道了这个性质之后就很好实现判断两条线段是否有交点了。注意到两条线段 \(AB,CD\) 没有交点的充要条件是 \(AB\) 全在直线 \(CD\) 的一侧,或者 \(CD\) 全在直线 \(AB\) 的一侧,写个叉积判断下即可。
bool inter(point x1,point y1,point x2,point y2){
return (sgn((x2-x1)|(y2-x1))!=sgn((x2-y1)|(y2-y1)))
&&(sgn((x1-x2)|(y1-x2))!=sgn((x1-y2)|(y1-y2)));
}
向量的旋转
这个乍一看不太好实现,不过注意到我们学过一个东西叫做复数,对于向量旋转这类牵扯到幅角的运算,可以转化为向量乘法的模长相乘,幅角相加,对于向量 \(\vec{u}=(x,y)\),我们记 \(u\) 对应的复数 \(z=x+yi\),那么旋转后对应的复数 \(z'\) 需满足 \(|z'|=|z|,\arg z'=\arg z+\theta\),其中 \(\theta\) 为旋转角,根据伏地魔定理,\(z'=z\times(\cos\theta+i\sin\theta)\),随便算一算就行了。
点在直线上
这个就非常 trival 了,显然对于两个向量 \(\vec{PA},\vec{PB}\),\(\vec{PA}\times\vec{PB}=0\) 当且仅当 \(P,A,B\) 三点共线,因此我们只需检验 \(\vec{PA}\times\vec{PB}=0\) 是否满足即可。
计算点到直线的距离
对于直线 \(l\) 外一点 \(P\) 和直线 \(l\) 上两点 \(AB\),根据向量叉积的几何意义,\(|\vec{PA}\times\vec{PB}|\) 的几何意义就是 \(\triangle ABP\) 面积的两倍,再除以 \(AB\) 的长即可得到 \(P\) 到 \(AB\) 的距离。
u1s1 用叉积解计算几何题就是方便,比那种暴力求出直线方程再代入坐标公式的做法不知道高明到哪里去了
计算两直线交点坐标
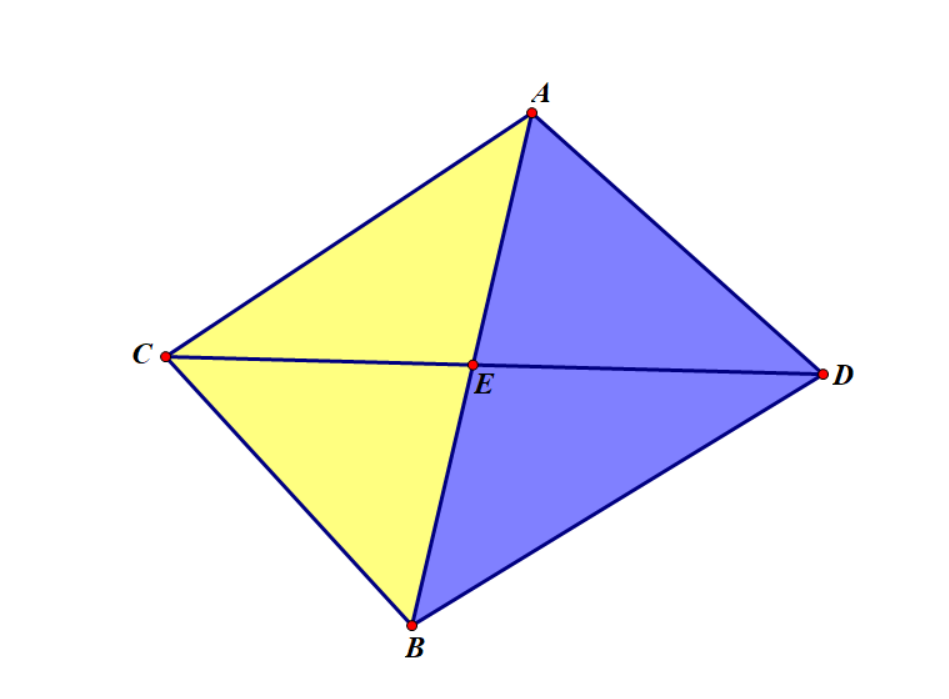
以下图为例,假设我们要求 \(AB,CD\) 的交点 \(E\),那么根据小学奥数有 \(\dfrac{S_{\triangle ABE}}{S_{ABCD}}=\dfrac{CE}{CD}\),而根据向量叉积的集合意义,\(S_{\triangle ABE}=\dfrac{\vec{CA}\times\vec{CB}}{2}\),\(S_{ABCD}=\dfrac{\vec{AB}\times\vec{CD}}{2}\),故 \(\dfrac{CE}{CD}=\dfrac{S_{\triangle ABC}}{S_{ABCD}}=\dfrac{\vec{CA}\times\vec{CB}}{\vec{AB}\times\vec{CD}}\),因此可以推得 \(\vec{CE}=\vec{CD}\times\dfrac{\vec{CA}\times\vec{CB}}{\vec{AB}\times\vec{CD}}\),这样即可求出 \(E\) 的坐标。
例题:
1. P1153 点和线
我为什么要刷这样的题
直接暴力 next_permutation 枚举全部情况,判断线段之间两两是否有交点即可。
时间复杂度 \(\mathcal O((n-1)!n^2)=\mathcal O(n!n)\)
2. P1354 房间最短路问题
显然每次改变方向的点只可能位于某段墙的边缘,于是将每段墙看作一个点,求出两两之间的距离暴力 floyd 即可。
3. P3217 [HNOI2011]数矩形
ymx 鸽鸽强强,ddw!
考虑枚举对边,那么两条线段 \(AB,CD\) 可以成为一个矩形的对边当且仅当:
- \(AB//CD\),叉积判断
- \(AC\perp AB\),点积判断
- \(AB=CD\)
我们将所有线段按长度为第一关键字排序,如果长度相同则通过 \(\vec{AC}·\vec{AB}\) 的符号排序,如果 \(\vec{AC}·\vec{AB}=0\) 则按 \(\vec{AB}\times\vec{CD}\) 排序,那么显然排完序后符合条件的线段一定构成一段连续段,而其中面积最大的矩形一定位于连续段的端点,双针扫一遍即可。
时间复杂度 \(n^2\log n\)。
极角排序
极角排序在计算几何中是一个非常实用的 trick,给定平面直角坐标系上 \(n\) 个向量,把这 \(n\) 个向量按 \(x\) 轴正半轴与其的夹角从小到大排好序的过程,就叫极角排序。
极角排序的方式有两种,一是直接调用 atan2 函数求出向量的幅角然后从小到大排序,优点是实现方便,缺点是常数大+容易爆精度。二是使用叉积正负判断向量之间的相对位置,但是朴素的叉积无法排整个平面直角坐标系内的向量,因为对于三个向量 \(\vec{u},\vec{v},\vec{w}\),如果 \(\vec{u}\times\vec{v}>0,\vec{v}\times\vec{w}>0\),并不能得出 \(\vec{u}\times\vec{w}>0\)(反例:单位圆的三等分点),因此需要先求出每个点所在的象限,对于同一象限中的点,就可以直接向量叉积判断了,优点是精度小,缺点是实现有点冗余。(当然如果题目规定所有向量都在过原点的某条直线的同侧,那就可以直接叉积判断)
例题:
4. CF598C Nearest vectors
mol ban tea,直接排一下扫一遍即可,注意精度问题。
5. P2992 [USACO10OPEN]Triangle Counting G
考虑容斥,拿总三角形个数 \(\dbinom{n}{3}\) 减去不符合要求的三角形个数即是答案。因此我们只需求出不符合要求的三角形个数即可,我们假设不符合要求的三角形的三个顶点按极角排序分别是 \(i,j,k\),那么以 \(i,j,k\) 为顶点的三角形当且仅当 \(i,k\) 的夹角 \(<\pi\),因此考虑枚举 \(i\),双针找出合法的 \(k\) 的最大值 \(k_{\max}\),那么 \(j,k\) 可以在 \([i,k_{\max})\) 中取值,组合数算一下即可。
6. P3476 [POI2008]TRO-Triangles
卡常屑题爬(大雾
考虑枚举三角形的一个顶点 \(A\),那么对于三角形的另外两个顶点 \(B,C\),对答案的贡献 \(S_{\triangle ABC}=\dfrac{|\vec{AB}\times\vec{AC}|}{2}\),我们记 \(\vec{v_i}=\vec{Ai}\),那么 \(S_{\triangle ABC}=\dfrac{|\vec{v_B}\times\vec{v_C}|}{2}\),考虑将这些向量极角排序并枚举极角较小的一个点 \(B\),那么满足 \(\vec{v_B}\times\vec{v_C}>0\) 的点 \(C\) 一定在区间内,双针绕一圈找出来,这样即可将绝对值去掉。再根据 \(\vec{u}\times\vec{v}=x_uy_v-x_vy_u\) 得 \(\vec{v_B}\times\vec{v_C}=x(v_B)y(v_C)-x(v_C)y(v_B)\),而 \(x(v_B),y(v_B)\) 都是常数,因此可以预处理 \(x(v_C),y(v_C)\) 的前缀和 \(\mathcal O(1)\) 计算贡献。最终答案除以 \(6\) 即可。复杂度 \(\mathcal O(n^2\log n)\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号