点分治学习笔记
大家好,今天我们来聊聊淀粉质点分治。又开了个有点大的坑(
点分治是一种针对树上路径问题的强有力的算法。一般看到与树上任意两点之间的路径有关的问题,那这题八成就是点分治了。那么点分治究竟是个什么玩意儿呢?我们不妨先来看道例题:P3806 【模板】点分治1
首先暴力地枚举所有点对是 \(n^2\log n\) 的,一脸过不去,考虑进行一些优化。我们随便定一个根 \(rt\),将这棵无根树变成一棵有根树。这样所有路径可分为两类:
- 经过根节点的路径
- 不经过根节点的路径。
对于第一类路径,显然它的两个端点 \(u,v\) 应当位于根节点的两个不同子树中,否则它就不经过 \(rt\) 了。当然 \(u,v\) 也可以等于 \(rt\),所以可以把根节点这一个点也单独地看作“根节点的一个子树”。我们记 \(dis_i\) 为根节点到节点 \(i\) 路径的长度。那么 \(u,v\) 之间的距离就是 \(dis_u+dis_v\)。我们的目标就是找出是否存在某两个位于根节点的不同子树中的节点 \(u,v\) 满足 \(dis_u+dis_v=k\)。
考虑开个桶 \(c_i\) 维护在当前已经访问过的节点中 \(dis_u=i\) 的 \(u\) 是否存在,初始只有 \(c_0=1\),因为 \(dis_u=0\)。枚举根节点的每个子树 \(u\),DFS 一遍求出子树 \(u\) 内的每个节点的 \(dis\) 值,然后枚举子树 \(u\) 内的每个节点 \(x\),如果 \(c_{k-dis_x}=1\),那么就证明存在某个 \(y\) 使得 \(x,y\) 不属于同一棵子树,并且满足 \(dis_y=k-dis_x\),即 \(dis_x+dis_y=k\),故也就存在某个第一类路径满足其长度等于 \(k\)。
最后再对于 \(u\) 子树内所以节点 \(x\) 更新 \(c_{dis_x}=1\)。显然这种做法能包含所有的第一类路径,这样可以在 \(\mathcal O(|\text{size}|)\) 的时间内搞定第一类路径,其中 \(\text{size}\) 为树的大小。你可能会好奇为什么不直接一遍 DFS 并直接把所有结点的 \(c_{dis_x}\) 更为 \(1\),或者为什么不先更新桶再计算贡献。因为这样会导致 \(u,v\) 可能在根节点的同一子树中,它们之间的路径长度本不应该不是 \(dis_u+dis_v\) 却满足 \(dis_u+dis_v=k\),这种情况本不符合题意却被我们计算了。
对于第二类路径,显然这个路径上所有的点都在根节点的某个子树中,故可以通过递归根节点的子树将第二类路径转化为第一类路径。但是很遗憾的是,这个算法随便一叉就能把它卡到 \(n^2\),比如说当树退化成一条链的时候,需要递归 \(n\) 次,每次递归时子树大小都是 \(\mathcal O(n)\) 级别的。
这时注意到我们的算法中有个漏洞,那就是“随便定一个根”。还是回到一条链的情况,如果我们不简简单单地以 \(1\) 号节点,而是以链的中点为根。并且每次递归的时候也以对应的链的中点为根,那么递归的深度就只有 \(\log n\) 级别,总复杂度也不过 \(n\log n\)。这样看来,选好这个根节点至关重要,如果我们碰巧选对了根节点,那可以大大降低算法的复杂度。那么这个根究竟该怎么选呢?考虑每次递归的时候以当前子树的重心为根,这样去掉根节点之后子树的大小就可以尽量平衡了。
这样复杂度是否就对了呢?还真是。注意到重心的一个性质,那就是删掉重心后子树大小不超过 \(\dfrac{n}{2}\),这样每次递归子树大小减半,递归深度就只有 \(\log n\) 了。总复杂度 \(n\log n\)。
口胡起来非常容易,然而一写代码,漏洞百出。下面给出模板题的代码,易错点都已用注释的形式标出:
int mx[MAXN+5],siz[MAXN+5],cent=0;//mx表示去掉点x之后剩余子树大小的最大值,siz表示当前子树的最大值,cent表示重心编号
bool vis[MAXN+5];
int dis[MAXN+5];
int sub[MAXN+5],subn=0;//sub表示当你枚举根节点的子树u的时候,u子树内的所有节点
int all[MAXN+5],alln=0;//all表示所有在根节点子树内的节点
bitset<MAXW+5> hav;//bitset优化空间,hav就是上文中提到的桶c[i]
bool ans[MAXQ+5];
void findroot(int x,int f,int tot){//找重心,tot表示整棵子树的大小
siz[x]=1;mx[x]=0;//易错点1!注意清空
for(int e=hd[x];e;e=nxt[e]){
int y=to[e];if(vis[y]||y==f) continue;//易错点2!不能只习惯性判y==f,还要判y是否未被递归到
findroot(y,x,tot);chkmax(mx[x],siz[y]);siz[x]+=siz[y];
} chkmax(mx[x],tot-siz[x]);
if(mx[x]<mx[cent]) cent=x;//更新重心
}
void getdis(int x,int f){//求出根节点到子树内每个点的距离dis[i]
sub[++subn]=x;
for(int e=hd[x];e;e=nxt[e]){
int y=to[e],z=cst[e];if(vis[y]||y==f) continue;//同上
dis[y]=dis[x]+z;getdis(y,x);
}
}
void solve(int x){//计算经过x的路径的答案
alln=0;all[++alln]=x;dis[x]=0;hav[0]=1;//注意清空
for(int e=hd[x];e;e=nxt[e]){//枚举根节点的每一个子树u
int y=to[e],z=cst[e];if(vis[y]) continue;
subn=0;dis[y]=z;getdis(y,x);//求出u子树内的所有点到根节点的距离
for(int i=1;i<=subn;i++) for(int j=1;j<=qu;j++)
if(q[j]>=dis[sub[i]]&&hav[q[j]-dis[sub[i]]]) ans[j]=1;//如果存在某个u子树内的点v满足c[k-dis[v]]=1那么就说明存在长度为k的路径
for(int i=1;i<=subn;i++) hav[dis[sub[i]]]=1;//易错点3:先算贡献再更新桶,否则会出现u,v属于同一棵子树,它们之间路径的长度不是dis[u]+dis[v],却被累加进答案的情况
for(int i=1;i<=subn;i++) all[++alln]=sub[i];//将所有sub[i]压入all中,方便最后的情况
}
for(int i=1;i<=alln;i++) hav[dis[all[i]]]=0;//易错点4!不要直接memset!
}
void divcent(int x,int tot){
vis[x]=1;solve(x);//计算第一类路径的贡献
for(int e=hd[x];e;e=nxt[e]){//分治调用divcent函数
int y=to[e];if(vis[y]) continue;
cent=0;int szy=(siz[y]<siz[x])?siz[x]:(tot-siz[x]);//算y子树的大小
findroot(y,x,szy);divcent(cent,szy);//易错点5!这里的cent很容易习惯性写成y
}
}
int main(){
/*读入*/
mx[0]=INF;/*易错点6!记得把mx[0]初始化成INF*/findroot(1,0,n);divcent(cent,n);
}
1. P2634 [国家集训队]聪聪可可
mol ban tea,等价于求有多少个路径满足权值之和为 \(3\) 的倍数,每次以当前分治中心为根,然后开个大小为 \(3\) 的桶 \(buc_x\) 表示有多少个点到根节点路径 \(\bmod 3=x\),还是边遍历边更新桶即可。
2. P4149 [IOI2011]Race
mol ban tea \(\times 2\),考虑每次以当前分治中心为根,经过根的路径的贡献可以转化为两个端点的深度之和。我们记 \(buc_x\) 为所有到根节点路径上权值和为 \(x\) 的路径中,深度的最小值,直接边遍历子树边更新 \(buc_x\) 即可,时间复杂度 \(n\log n\)。
3. P2993 [FJOI2014]最短路径树问题
考虑如果已经知道这个“最短路径树”之后怎样求得答案。很明显可以用点分治,比如说我们正在处理以 \(rt\) 为根的子树。对于不在 \(rt\) 同一个子树中的两点 \(u,v\),它们路径的点数为 \(dep_u+dep_v+1\),路径长度为 \(dis_u+dis_v\)。还是从左到右枚举 \(rt\) 的所有子树。记录一个桶 \(c_i\) 表示对于已经访问过的子树的节点 \(u\) 满足 \(dep_u=i\) 当中,\(dis_u\) 的最大值。然后用 \(dis_i+c_{k-1-dep_i}\) 更新答案即可。
最后考虑怎么求出“最短路径树”,其实你只用在求最短路的时候记录一个前驱 \(pre_i\),如果有多个 \(pre_i\) 就取最小的 \(pre_i\),然后在 \(i\) 与 \(pre_i\) 之间连边就可以得到这个最短路径树了,之前做过道类似的题 P6880 [JOI 2020 Final] オリンピックバス。
老缝合怪了
4. P6329【模板】点分树 | 震波
从这题开始,就有刷不完的毒瘤题了
首先我们知道,单次询问,树上路径的问题可以用点分治解决。但如果加上什么 \(q\) 次询问之类的东西怎么办呢?比如说这题。显然每次都跑一遍点分治时间复杂度肯定吃不消。考虑把点分治的过程离线下来,将当前树的重心与上一层的树的重心连边,这样就可以得到一棵树,我们称之为“点分树”。
比如说我们有如下图所示的树:
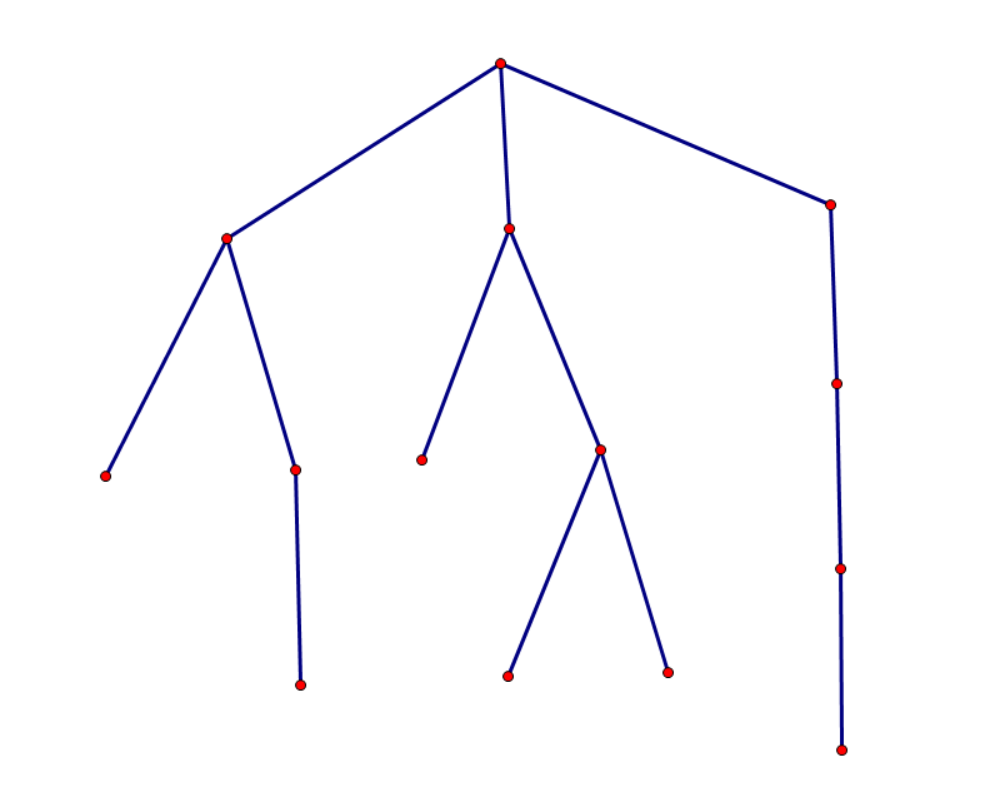
建出点分树来如下图所示:
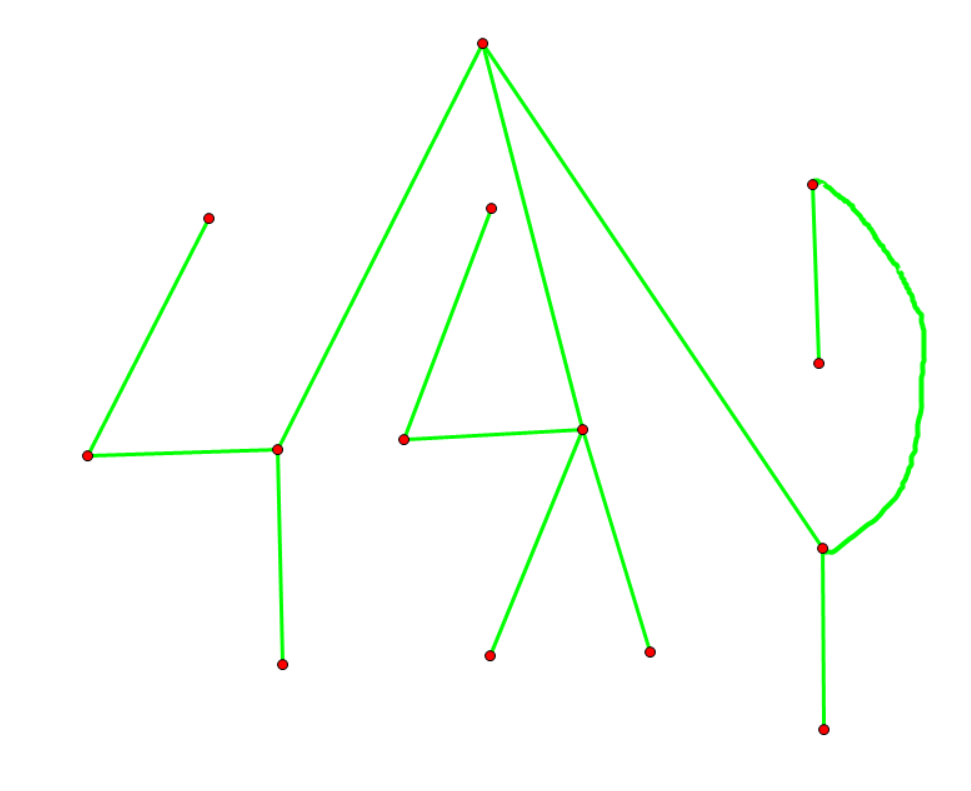
很明显,我们建出的点分树与原树几乎没有联系,父子关系完全被打乱了,也无法通过两点在点分树上的距离算出它们在原树上的距离。甚至有可能某两点在点分树上是父子关系,在原树上相隔十万八千里,或者某两点在原树上是父子关系,在点分树上相隔十万八千里(当然只是相对来说)。
那么这棵树对于我们做题有什么帮助呢?
有的问题我们不是非常关心树的形态特点,比如路径问题,联通块问题,寻找关键点问题等等,以路径问题为例,我们不一定非得查到 \(p,q\) 的 LCA 才可以处理 \(p,q\) 的路径信息,相反,我们可以随便从这个路径上寻找一个分割点 \(t\),只要我们可以快速的处理 \(p\) 到 \(t\) 和 \(q\) 到 \(t\) 的信息,我们就可以处理 \(p\) 到 \(q\) 的信息。
而点分树恰恰就是对原树做了这样的映射。
它有以下性质:
- 它的高度与点分治的深度一样,只有 \(\log n\) 级别,这个性质很关键,由于它的高度只有 \(\log n\),所以我们可以搞出各种各样在一般树论里过不去的暴力做法,比如说对每个点开个包含子树中所有点的 vector,空间复杂度也只有。
- 对于任意两点 \(u,v\),唯一可以确定的是 \(u,v\) 在点分树上的 LCA 一定在 \(u\to v\) 的路径上。换句话说,\(dis(u,v)=dis(u,lca)+dis(lca,v)\)。
回到这题来,我们要求 \(\sum\limits_{dis(x,y)\leq k}a_y\)。
考虑枚举 \(x,y\) 在点分树上的 LCA \(z\)(这显然是 \(\log n\) 级别的),根据上面的推论有 \(dis(x,y)=dis(x,z)+dis(y,z)\)。
故 \(ans=\sum\limits_{dis(x,z)+dis(z,y)\leq k \and LCA(x,y)=z}a_y=\sum\limits_{dis(z,y)\leq k-dis(x,z) \and LCA(x,y)=z}a_y\)
考虑什么样的 \(y\) 满足 \(LCA(x,y)=z\),显然符合要求 \(y\) 组成的集合就是 \(z\) 的子树抠掉 \(z\) 在 \(x\) 方向上的儿子 \(s\) 的子树。而我们要求这个点集中到 \(z\) 的距离 \(\leq k-dis(x,z)\) 的点权和。显然可以拿 \(z\) 的子树内到 \(z\) 的距离 \(\leq k-dis(x,z)\) 的点权和 \(-\) \(s\) 子树中到 \(z\) 的距离 \(\leq k-dis(x,z)\) 的点权和。对每个点 \(x\) 建一棵动态开点线段树,下标为 \(i\) 的位置维护 \(x\) 子树内所有 \(dis(x,z)=i\) 的 \(a_z\) 的和。那么求 \(z\) 子树内到 \(z\) 的距离 \(\leq k-dis(x,z)\) 的点权和就在对应线段树上查个区间和就 ok 了。
那 \(z\) 在 \(x\) 方向上的儿子 \(s\) 的子树怎么办呢?
初学点分树的萌新(例如我)很容易进入一个误区,那就是这东西可以在 \(s\) 对应的线段树上查 \([0,k-dis(x,z)-1]\) 的和。但这显然是错的,因为两点在点分树上的距离与两点在原树上的距离没有一丁点联系。到 \(s\) 距离 \(\leq k-dis(x,z)-1\),并不意味着到 \(z\) 距离 \(\leq k-dis(x,z)\)。那么正解是什么呢?考虑对于每个点再建立一棵动态开点线段树,线段树上下标为 \(i\) 的位置维护 \(x\) 子树内到 \(fa_x\) 距离 \(=i\) 的点权和。解决 \(z\) 在 \(x\) 方向上的儿子 \(s\) 的子树的问题只需在点 \(s\) 的线段树上查询 \([0,k-dis(x,z)]\) 的和就行了。
5. P2056 [ZJOI2007]捉迷藏
考虑这题只有一组询问的版本,很明显一个简单的静态点分治。假设我们考虑以 \(rt\) 为根的子树,对于 \(rt\) 的每个子树,求出这个子树内的点到 \(u\) 距离的最大值,并将其压入一个 multiset,那么该点对答案的贡献就是 multiset 中最大的两个数之和(类似于树的直径)
回到原题。既然多组询问,就先建出点分树出来。借鉴简化版的做法,对于每个点建一个 multiset \(st_x\) 维护该点的所有子树中到该点距离的最大值的集合。那么怎么维护这个最大值呢?对每个点再建一个 multiset 叫 \(dists_x\),维护 \(x\) 子树中所有点到 \(fa_x\) 的距离,然后每次修改就先改动 \(dists_x\)(最多改 \(\log n\) 个 \(dists_x\)),然后再修改对应的 \(st_x\),最后更新答案。时间复杂度 \(n\log^2n\)
当然,此题正解并不是动态点分治,还有更优的 \(1\log\) 的做法。并且该做法由于常数巨大被卡常了,不吸氧 TLE 80,吸氧 TLE 90。
6. CF566C Logistical Questions
nb tea,题解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号