2507 题目总结集合
目录
期末(一)
T1 数列维护
题目描述
给定一个序列\(A=(a_i)\),可以进行一次操作——将一个数\(a_i\) 提前,求操作后所有序列的子序列字典序最大的一个。
\(1\le|A|\le2\times10^5, \sum{|A|}\le10^6\),多测\(100\).
题目分析
考虑贪心:
- 将原序列按照大序排序并记下原来下标;
- 若新序列\(a'_i \ge a'_{i+1}, pos_i < pos_{i+1}\) 则直接取用;
- 若\(a'_i \ge a'_{i+1}, pos_{i-1} < pos_{i+1} < pos_i\) 则取用(本条只能使用一次);
- 舍弃。
最后所选即为答案。
证(\(\text{k\v ou}\))明(\(\text{h\'u}\))
到第一个按序但在后的点可以使用一次提前,并一定比提前后面的点字典序更大。
T2 作业
题目描述
\(N\) 个区间\((s_i,t_i)\),表示区间\(i\) 长度\(t_i\),开始位置在\(s_i\) 之前(包括,且全局左端点是\(0\))。
求在区间不重合的情况下最多可以存在多少个。
\(0\le s_i\le10^{18}, 1\le t_i\le10^{18}, 1\le N\le 2\times10^5, \sum{N}\le 3\times10^5\),多测\(10\).
题目分析
按照 \(s_i+t_i\) 升序排序,得到每个区间的最右可能结束位置。
维护当前选择的所有区间。
考虑新加入一个区间:
- 如果区间塞得下,则加入;
- 若塞不下,考虑删去当前选择的区间中长度最大的。
证明
考虑可行性:
- 对于删去旧大区间加入新区间的行为:因为最后一段一定为合法开始,结尾不降,按次尝试,且长度不大于最大旧区间,则删去后一定可以空出一段在合法开始之前的位置。
考虑正确性:
- 看似正确,但不会证,留空待补。
期末(二)
T1 花匠
题目背景
NOIP2013 提高组 D2T2
题目描述
选取原序列的最长子序列,使得新序列成为“波浪形”,求新序列长度。
$ 1 \le n \le 10^5 $.
题目分析
求原序列所有“拐点”(水平算一个)。
考虑若选择不是拐点,而是拐点 \(-x\), 则拐点右侧拐点 \(-x\) 以上不能选取,答案不优。
T2 ⽕柴排队
题目背景
NOIP2013 提高组 D1T2
题目描述
重排两个等长序列 \(A, B\) 使得 \(\sum{(A_i-B_i)^2}\) 最小。
重排过程中每次选择一个序列的两个相邻位置交换,求最小交换次数。
\(1\leq n\le10^5, a_i\ne a_j, b_i\ne b_j, i\ne j\).
题目分析
考虑将两个序列排序,一一对应,求新的序列中每对元素原位置逆序对的数量。
证明(一)
考虑两对元素 \((a,b),(a-p,b-q), p,q\ge0\),其贡献为 \(2(a-b)^2+2(a-b)(q-p)+(q-p)^2\);
考虑交换顺序 \((a-p,b),(a,b-q)\),则贡献变为 \((a-b)^2-2p(a-b)+p^2+(a-b)^2+2q(a-b)+q^2=2(a-b)^2+2(a-b)(q-p)+p^2+q^2\);
因为 \(p,q \ge 0\), 所以 \(p^2+q^2 \ge (q-p)^2\),即“排序不等式”。
证明(二)
考虑折线 \(\alpha:a_i,\beta:b_i\),\(\sum{(A_i-B_i)^2}\) 即为 \(\alpha\) 对 \(\beta\) 的离散程度(类比方差)。
现在已知对应关系,求相邻互换最小步数,逆序对解决即可。
T3 Hankson 的趣味题
题目背景
NOIP 2009 提高组 第二题
题目描述
给定 \(a_0, a_1, b_0, b_1\) 求满足 \(\gcd(x,a_0)=a_1,\text{lcm}(x,b_0)=b_1\) 的正整数 \(x\) 的数量。
\(1\le a_0,a_1,b_0,b_1\le 2\times 10^9, a_1 | a_0, b_0 | b_1\),多测 \(2000\).
题目分析
直接质因数分解,看因数个数差计算得。
T4 赛道修建
题目背景
NOIP 2018 提高组
题目描述
将一棵带边权的无根树沿边分出 \(m\) 条没有重合边的路径,使得所选路径中最小长度最大,求最大最小长度。
题目分析
特殊性质(一)
\(m=1\)
即求树直径。
特殊性质(二)
是菊花图
二分答案并验证。考虑将边以权值从小到大排序:
- 若边权本身不小于猜测值,则取用;
- 若不足则寻找最小的边使得和不小于猜测值,取用二者。
- 若足够取用 \(m\) 条(对),则当前猜测值满足;
- 若取完后依旧不足,则该值不行。
特殊性质(三)
是二叉树
考虑二分答案并贪心验证:
\(\text{DFS}\) 从下到上传递完结的线段个数和余下的最大路径长度。
整体
同特殊性质(二)+特殊性质(三)
NOIP 模拟
T1 竞选预测
题目描述
有 \(X\) 个人竞选 \(Y\) 个议会席位,共有 \(N\) 位公民依次为他们投票,每位公民必须从 \(X\) 个竞选者中选出一人投票给他。
这 \(X\) 个人将通过投票结果排位。获得至少一张选票的竞选者中,排名最靠前的 \(Y\) 位胜出。若获得至少一张选票的竞选者不足 \(Y\) 人,则只有这些人能够入选。
排位以票数高者排名靠前,票数相同时则较早收到最后一张选票的人排名靠前。
现在已知前 \(M\) 位公民的投票结果,考虑预测最终的竞选结果。对于一位竞选者来说,如果:
- 之后无论如何投票,他都无法入选,则其结果记为 \(−1\);
- 之后无论如何投票,他都能入选,则其结果记为 \(1\);
- 否则表示他的竞选结果无法确定,则其结果记为 \(0\);
预测时对每位竞选者独立做预测,依次输出对每位竞选者的预测结果。
题目分析
判断前 \(Y\) 个人是否一定当选:
- 当且仅当此人不为 \(0\),且即使剩下选票全部分配给其后到 \(Y+1\) 人,还不足以将其挤出 \(Y\) 名,则为必胜。
- \(N-M \ge (Y-pos)\times a_pos - \sum_{i=pos+1}^{Y+1}{a_i}\) 且 \(a_{pos} \ne 0\).
判断后面的人是否一定不当选:
- 如果剩下的选票都得到,还是不能挤掉第 \(Y\) 个人,则必败。
- \(N-M <= a_Y-a_{pos}\).
当 \(M = N\) 时,投票结果确定,排序即可。
DP 题单
数字序列
题目背景
河南省选 2006
题目描述
现在我们有一个长度为 \(n\) 的整数序列 \(a\)。但是它太不好看了,于是我们希望把它变成一个单调严格上升的序列。但是不希望改变过多的数,也不希望改变的幅度太大。
第一行输出一个整数,表示最少需要改变多少个数。
第二行输出一个整数,表示在改变的数最少的情况下,每个数改变的绝对值之和的最小值。
- 对于 \(90\%\) 的数据,保证 \(n \leq 6 \times 10^3\)。
- 对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 3.5 \times 10^4\),\(1 \leq a_i \leq 10^5\)。数据保证 \(a_i\) 随机生成。
题目分析
问题(一)
因为严格上升,所以 \(a_i < a_{i+1}\).
我们考虑保留最多的数,是的保留的数的位置 \(p_i\) 有 \(a_{p_{i+1}} - a_{p_i} \ge p_{i+1} - p_i\),即对于新序列 \(b_i = a_i - i\) 求最长上升子序列。
\(\Theta(n \log n)\)
问题(二)
记录最长上升子序列的每个点,考虑对两点之间的点移动。
由于最长上升子序列,所以中间点必在区间 \([a_{p_i},a_{p_{i+1}}]\) 外,则点移动到 \(a_{p_i}\) 或 \(a_{p_{i+1}}\) 上的答案更优。
由于单调,所以考虑一个位置,使得其前点为 \(a_{p_i}\),后为 \(a_{p_{i+1}}\),枚举得到最小值。
\(\Theta(n)\)
但是 最长上升子序列可能有多种情况。
我们考虑每次转移更新 \(dp_i \to dp_{i+1}\) 时建边,将对应值当作点,从上到下连接单向边。如下图:
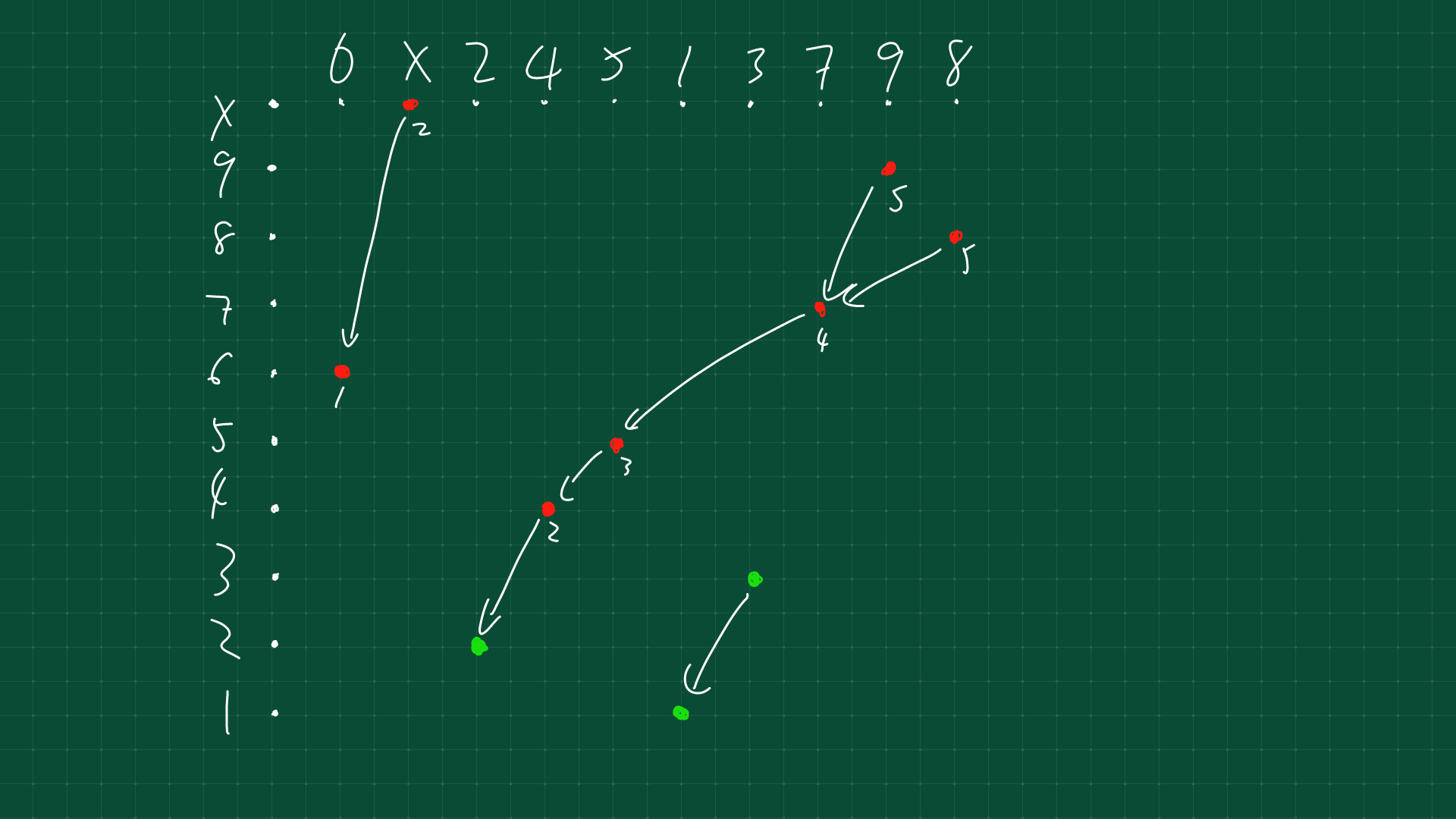
在得到最长上升子序列长度后记录所有以此结尾的点,为“开始点”,
从“开始点”开始 \(\text{DFS}\),记录所有“开始点”的路径,即为所有方案(如图中 \(\{2,4,5,7,9\},\{2,4,5,7,8\}\) 两条路径)。
\(\Theta(n^2)\)
当然,可以建立无穷小的超级点,反向建边遍历。
不想写代码
背包集合
0/1 背包
P1048 [NOIP 2005 普及组] 采药
P1060 [NOIP 2006 普及组] 开心的金明
P1855 榨取kkksc03
板子
完全背包
板子
分组背包
单层少依赖背包
本题只有一层依赖关系,且每个物品最多只有两个子物品。
所以考虑对于每个主物品分四种情况:只选主物品、选主+子A、选主+子B、选主+AB,分别求重量和价值。
正常做 0/1 背包(由于重量不一样,记得滚动数组)。
\(\Theta(nw)\)
单层多依赖背包
仍然是只有一层,那么考虑分层做背包。
设数组 \(g_{i,j}\) 表示对于第 \(i\) 个主物品,其花费 \(j\) 的重量获得的最大价值。
然后对数组 \(g_{i,j}\) 做 0/1 背包(由于重量不一样,记得滚动数组)。
\(\Theta(nw^2)\)
多层依赖背包
按照依赖关系建立树形结构(没有依赖的物品认为依赖于一个 \(0\) 大小 \(0\) 价值的“超级物品”)。
\(\text{DFS}\) 从下到上,数组 \(g_{i,j}\) 表示对于第 \(i\) 个物品,其花费 \(j\) 的重量获得的最大价值。
直接每层做背包。
\(\Theta(nw^2)\);一些题目实际最大空间和子树叶子/节点数量有关,其可能为 \(\Theta(n^2)\)。
组内单选背包
板子
泛化背包
先解决子问题,后合并。
对于每个物品 \(i\) 定义价值函数 \(V_i(j)\) 表示花费 \(j\) 的空间获得的最大价值。
按照 多层依赖背包 所述转移。
\(\Theta(nw^2 V)\)
其他
题目描述
初始总共有 \(n\) 个人,每个人的体力值为 \(a_i\) ,当第 \(i\) 个人体力值降为 \(0\) 的时候,第 \(i\) 个人就会下场。
假设第 \(i\) 个人和第 \(j\) 个人决斗,则两者体力值均减掉 \(min(a_i,a_j)\)。当最后只有一个人站在场上,那个人就获胜了。当然既然是 nobe 大师的作品怎么可能像小程序游戏一样唐?假设现在有 \(m\) 个人,雨野可以选择一个长度为 \(m\) 的排列 \(p\),则每次在排列中选取前两位还没有下场的人进行决斗直到最后只剩一个人站在场上,如果没有人站在场上,那就没有人获胜。
同时这个游戏还支持自定义角色,雨野自定义了 \(q\) 个角色,他决定依次将这些角色加入游戏中,在加入第 \(i\) 个角色之后他想立刻知道现在第 \(i\) 个角色是否有可能获得胜利,如果可以,输出
mono并构造方案,否则输出nobe。
题目分析
首先要想一个人赢,应当放在最后,等前面所有人打完后剩下一个“残血”的打。然后考虑如何让最后剩下的这个人血最少。
因为一次只有两个人打,且不会共赢,我们考虑将所有人分成两组,相互之间打。
设 \(f_{i, 0/1}\) 表示考虑到第 \(i\) 个人,其放在第 \(0/1\) 组所产生代价的最小值。我们发现其一定会放在体力和更小的一组。
老师说这是背包,但没我看出来
\(\Theta(n)\)
骑士
题目背景
[ZJOI2008]
洛谷 P2607
题目描述
[P3177 [HAOI2015] 树上染色](https://www.luogu.com.cn/problem/P3177)
[ [ZJOI2008] ](https://www.luogu.com.cn/problem/P2607)
[P3698 [CQOI2017] 小Q的棋盘](https://www.luogu.com.cn/problem/P3698)
[P5658 [CSP-S2019] 括号树](https://www.luogu.com.cn/problem/P5658)
DP 大礼包
T2 KON-Ticket Inspector
题目背景
POI 2009
题目分析
考虑 \(f_{i,k}\) 表示在第 \(i\) 站后行驶过程中进行第 \(k\) 次检票。
由于一个人不会被多次计入答案,那么我们只需考虑在 \((j,i]\) 时上车且 \((i, n]\) 时下车的人,其中 \(j\) 表示上一次检票时间(没有则为 \(0\))。
可以用二位前缀和维护上下车人数 \(a_{i,j}\) 表示在 \((0,i]\) 上车且 \((0,j]\) 下车的总人数。
则 \(f_{i,k} = \max\limits_{j=1}^i f_{j,k-1} + a_{i,n} - a_{j,n} - a_{j, j} + a_{i,j}\)
\(\Theta(n^2k)\)
T4 DYN-Dynamite
注释
Cnblogs 文章中不能使用
⿰火乍⿱艹约这个词,原题中的所有⿰火乍⿱艹约包均使用 “TNT” 代替。
题目背景
POI 2011
洛谷 P3523
题目分析
原题是树形 \(\text{DP}\),但是我们可以尝试二分答案。
对于一个给定时间 \(T\),如果这个时间需要的点火点数量不超过 \(M\),那么更大的时间也肯定不足 \(M\);如果时间使得点火点数量超过 \(M\),那么更小的时间也肯定超过 \(M\)——可以二分。
考虑验证:
\(\text{DFS}\) 求出三元组 \((E, d, n)\) 分别表示子树有无TNT、最远没被点燃的TNT的距离、已经使用了几次着火点。
对于一个点,如果其所有子树的 \(\min d + \max d +2 \le T\) 那么认为这棵子树内部点燃点可以相互解决,返回 \((E, 1 + \min d, n)\);否则若 \(d\) 均不足 \(T\) 那么就返回 \((E, 1 + \max d, n)\);否则考虑在这个点放一个着火点,返回 \((E, 1-T, n+1)\)。
\(\Theta(n \log n)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号