前言
本博客部分参考 《具体数学》 一书.
本博客 基本 不需要任何高于初中数学的前置知识.
本博客作者数学很差,若有笔误请第一时间指正.
本博客的数学公式加了 \large,看起来不会很挤,为了保护你的视力,请在电脑上阅读.
问题
定义
\[\large
sq_n = \sum_{i = 1}^{n} i^2
\]
求 \(sq_n\) 的通项.
方法 0
要善于利用你的搜索引擎.
链接
于是可知 , 通项为 :
\[\large
sq_n = \frac{n(n + 1)(2n + 1)}{6}
\]
方法 1
这么个数列问题,首先考虑打个表.
| \(n\) |
0 |
1 |
2 |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| \(sq_n\) |
0 |
1 |
5 |
14 |
30 |
55 |
91 |
140 |
204 |
285 |
385 |
506 |
650 |
我们不妨构造一个函数\(f(x)\),使得:
\[\large
\begin{aligned}
f(0)=0 \\
f(1)=1 \\
f(2)=5 \\
f(3)=14 \\
f(4)=30 \\
f(5)=55 \\
f(6)=91 \\
f(7)=140 \\
f(8)=204 \\
f(9)=285 \\
f(10)=385 \\
f(11)=506 \\
f(12)=650 \\
\end{aligned}
\]
易得:
\[\large\begin{aligned}
f(x)= &\frac{22739}{1245404160} x^{13}
\\&-\frac{22739}{15966720} x^{12}
\\&+\frac{432041}{8709120} x^{11}
\\&-\frac{295607}{290304} x^{10}
\\&+\frac{39725033}{2903040} x^{9}
\\&-\frac{6798961}{53760} x^{8}
\\&+\frac{7154075963}{8709120} x^{7}
\\&-\frac{1092267865}{290304} x^{6}
\\&+\frac{26126269657}{2177280} x^{5}
\\&-\frac{9368672651}{362880} x^{4}
\\&+\frac{2932835723}{83160} x^{3}
\\&-\frac{150461191}{5544} x^{2}
\\&+\frac{682183}{78} x
\end{aligned}\]
其中:
\[\large
\begin{aligned}
f(13)=114514 \\
\end{aligned}
\]
所以,应填入空缺处的数字依次为:\(114514\).
大雾.
但是,观察力像 神 \(\mathrm{\color{black}{w}\color{red}{ind\_whisper}}\) 一样强的的人能看出,其通项是
\[\large
sq_n = \frac{n(n + 1)(2n + 1)}{6}
\]
那么考虑如何证明,采取 归纳法.
基础 : 对于 \(n = 0\) ,\(sq_0 = \frac{0}{6} = 0\) , 成立.
归纳 :
首先为了看着舒服把式子稍微变一下 :
\[\large
sq_n = \frac{n(n + 1)(n + \frac{1}{2})}{3}
\]
然后写出递归式 :
\[\large\boxed{\begin{aligned}
&sq_0 = 0,sq_1 = 1\\
&sq_n = sq_{n - 1} + n ^ 2
\end{aligned}}\]
两侧乘 3 :
\[\large\begin{aligned}
3 sq_n &= 3 sq_{n - 1} + 3n ^ 2\\
&= (n - 1)(n - 1 - \frac{1}{2})(n - 1 + 1) + 3n^2\\
&= n^3 + \frac{3}{2}n^2 + \frac{n}{2}\\
&=n(n^2 + \frac{3}{2}n + \frac{1}{2})\\
&= n(n + 1)(n + \frac{1}{2})
\end{aligned}\]
成立.
但是每次有类似问题都嗯猜属实拉跨,下面会介绍更泛用的方法,都以求平方和通项作为例子.
方法 2
扰动法 :
\[\large\begin{aligned}
sq_{n + 1} &= \sum_{i = 1}^{n + 1} i^2 \\
sq_n + (n^2 + 2n + 1) &= \sum_{i = 0}^{n} (i + 1)^2\\
&= \sum_{i = 0}^{n} (i ^ 2 + 2i + 1)\\
&= \sum_{i = 1}^{n} i^2 + 2\sum_{i = 0}^{n} (i + n + 1)\\
&= sq_n + n(n + 1) + n + 1
\end{aligned}\]
可以发现又推回去了,如蜜传如蜜啊.
但是发现把 \(sq_n\) 消掉后得到了求 \(\sum_{i = 1}^{n} i\) 的通项,也就是低一次的通项.
那么把要求的升级一下,定义 :
\[\large
cub_n = \sum_{i = 1}^{n} i^3
\]
考虑通过这个求出 \(sq_n\) 的通项.
\[\large\begin{aligned}
cub_{n + 1} &= \sum_{i = 1}^{n + 1} i^3\\
cub_n + (n + 1)^3 &= \sum_{i = 0}^{n} (i + 1)^3\\
&= \sum_{i = 0}^{n} (i ^3 + 3i^2 + 3i + 1)\\
&= cub_n + 3sq_n + 3\cdot \frac{n(n + 1)}{2} + (n + 1)
\end{aligned}\]
然后把 \(cub_n\) 消掉再移项就是通项了.
方法3
gg 说 : 格局打开.
现在直接把格局开大,直接推广这类递推式.
考虑建立一般模型 :
\[\large\begin{aligned}
R_0 &= \alpha\\
R_n &= R_{n - 1} + \beta + \gamma n + \delta n^2
\end{aligned}\]
将其解表示为 :
\[\begin{aligned}
R_n = A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta
\end{aligned}\]
然后 \(A(x),B(x),C(x),D(x)\) 和生成函数啥关系没有,别想多了.
首先,假设对于 \(R_n = 1\),有 :
\[\large\begin{aligned}
&A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = 1\\
&\therefore \alpha = 1,\beta = 0,\gamma = 0,\delta = 0. \therefore A(n) = 1
\end{aligned}\]
然后假设 \(R_n = n\), 有 :
\[\large\begin{aligned}
&A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n\\
&\therefore \alpha = 0,\beta = 1,\gamma = 0,\delta = 0. \therefore B(n) = n
\end{aligned}\]
然后假设 \(R_n = n^2\),有 :
\[\large\begin{aligned}
&A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n^2\\
&\therefore \alpha = 0,\beta = -1,\gamma = 2,\delta = 0. \therefore 2C(n) - B(n) = n^2\\
&\therefore C(n) = \frac{n(n + 1)}{2}
\end{aligned}\]
然后假设 \(R_n = n^3\),有 :
\[\large\begin{aligned}
&A(n)\alpha + B(n) \beta + C(n)\gamma + D(n)\delta = R_{n - 1} + \beta + \gamma n + \delta n^2 = n^3\\
&\therefore \alpha = 0,\beta = 1,\gamma = -3,\delta = 3. \therefore 3D(n) - 3C(n) + B(n) = n^3\\
&\therefore D(n) = \frac{n(n + 1)(n + \frac{1}{2})}{3}
\end{aligned}\]
这时候考虑原来的递推式,相当于\(\alpha = \beta = \gamma = 0,\delta = 1\) 的特殊情况,那么 :
\[\large
sq_n = D(n) = \frac{n(n + 1)(n + \frac{1}{2})}{3}
\]
方法 4
考虑 积分 .
首先,为了方便贴近我们要求的合式,积分可以形象化理解成求一个函数与 \(x\) 轴之间封闭图形的面积.
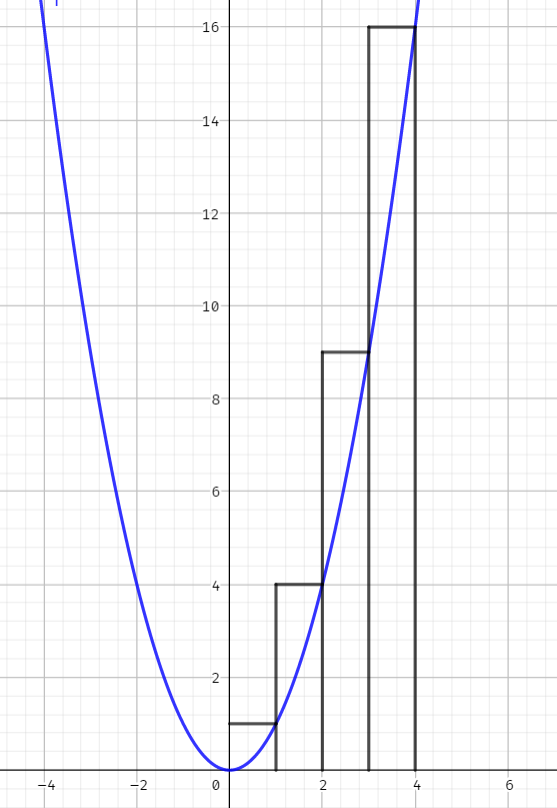
我们要求的是图中每个矩形面积的和,而图中蓝色 (是(0,0,255),别说什么你是全色盲,自己拿取色器看) 的抛物线是 \(y = x^2\) ,可以发现误差不大,考虑积分计算抛物线以下部分的面积.
然后用小学二年级(?)就有人告诉你的如下公式 :
\[\large\begin{aligned}
\int x^\mu dx = \frac{x^{\mu + 1}}{\mu + 1} + C ,(\mu \neq -1)
\end{aligned}\]
得出 :
\[\large
sq_n \approx \int_{0}^{n} x^2 dx = \frac{n^3}{3}
\]
然后要求更精确的解,就需要单独计算误差面积.
定义 :
\[\large
E_n = sq_n - \frac{n^3}{3}
\]
那么代入递推式 :
\[\large\begin{aligned}
E_n &= sq_n - \frac{n^3}{3}\\
&= sq_{n - 1} + n^2 - \frac{n^3}{3}\\
&= E_{n - 1} +\frac{1}{3} (n - 1)^3 + n^2 - \frac{n^3}{3}\\
&= E_{n - 1} + n - \frac{1}{3}
\end{aligned}\]
最后解出来 :
\[\large
E_n = \frac{3n^2 + n}{6}
\]
那么
\[\large
sq_n = E_n + \int_{0}^{n} x^2 dx = \frac{n(n + 1)(2n + 1)}{6}
\]
此方法最好的一点是求近似解可以推广 :
\[\large
\sum_{i = 1}^{n} i^k \approx \int_{0}^{n} x^k dx = \frac{x^{k + 1}}{k + 1}
\]
方法 5
奇怪的技巧之 : 展开和收缩 .
从加法展开后的形式上理解一下原本的合式 :
\[\large\begin{aligned}
\sum_{i = 1}^{n} (i \cdot i) &= (1 \cdot 1) + (2 \cdot 2) + \cdots + (n \cdot n) \\
&= 1 + 2 + 2 + 3 + 3 + 3 + \cdots + n + n + \cdots + n\\
&= \sum_{1 \le j \le i \le n} i\\
&= \sum_{j = 1}^{n} \sum_{i = j}^{n} i\\
&= \sum_{j = 1}^{n} \frac{(j + n)(n - j + 1)}{2}\\
&= \frac{1}{2} \sum_{j = 1}^{n} (n(n + 1) + j - j^2)\\
&= \frac{1}{2} n^2(n + 1) + \frac{1}{4}n(n + 1) - \frac{1}{2} sq_n
\end{aligned}\]
然后依然是移项即可求解.
或者如果你知道的话,可以用 阿贝尔恒等式 :
\[\large
\sum_{i = 1}^{n} a_ib_i = b_n\sum_{i = 1}^{n} a_i + \sum_{i = 1}^{n - 1} a_i\left( \sum_{j = 1}^{i} a_j \right) (b_i - b_{i + 1})
\]
方法 6
无限微积分的算子 \(D\) 可以理解为 \(D \to 0\) ,那么考虑运用 差分算子 的有限积分.
首先,有限微积分基于 差分算子\(\Delta\) :
\[\large
\Delta f(x) = f(x + 1) - f(x)
\]
为了更好的运用差分的性质,定义 上升幂 :
\[\large
x^{\overline{n}} = x(x + 1)(x + 2) \cdots (x + n - 1)
\]
定义 下降幂 :
\[\large
x^{\underline{n}} = x(x - 1)(x - 2) \cdots (x - n + 1)
\]
而且这个运算满足 :
\[\large
\Delta(x^{\underline{n}}) = nx^{\underline{n - 1}}
\]
也就是这是迎合差分的性质而创造的运算,当然我们在广义二项式里面也能看到它.
好的,现在让我们引入一个符号 :
\[\large
f(x) \vert^{b}_{a} = f(b) - f(a)
\]
那么对于有限微积分,有 :
\[\large
\sum_{a}^{b} \Delta f(x) \delta x = \left. f(x) \right|_{a}^{b}
\]
然后 :
\[\large
x^{2} = x^{\underline{2}} + x^{\underline{1}}
\]
于是对原来的和式做有限积分 :
\[\large\begin{aligned}
\sum_{i = 1}^{n} i^2 &= \frac{n^{\underline{3}}}{3} + \frac{n^{\underline{2}}}{2}\\
&= \frac{n(n + 1)(2n + 1)}{6}
\end{aligned}\]
方法 7
考虑 生成函数 .
众所周知有一个求数列前缀和的技巧是在其生成函数前乘上 \((1 - x)^{-1}\),本质上就是和 \(<1,1,1,1\cdots>\) 的 OGF 做卷积.
那么先写一个数列 \(<n^2>\) 的生成函数 :
\[\large
G(x) = \sum_{n = 0}^{\infty} n^2 x^n = \frac{x + x^2}{(1 - x) ^ 3}
\]
那么
\[\large\begin{aligned}
F(x) &= \frac{x + x^2}{(1 - x) ^ 4}\\
\end{aligned}\]
解一下 :
\[\large\begin{aligned}
\sum_{i = 1}^{n} i^2 &= [x^n]\frac{x + x^2}{(1 - x) ^ 4}\\
&= [x^n](x(1 + x)\sum_{k}\binom{k + 3}{3}x ^ k)\\
&= \binom{n + 1}{3} + \binom{n + 2}{3}\\
&= \frac{n(n + 1)(2n + 1)}{6}
\end{aligned}\]
方法 8
涉及基础微分,极限,导数知识,但是预习了必修3就能看懂吧大概
首先怎么想到用微分呢?
我们写一个 \(<1,1,1,\cdots>\) 的生成函数然后对其变形 :
\[\large
G(x) = \sum_{n = 0}^{\infty} x^n = 1 + x + x^2 + \cdots
\]
众所周知想要把一个因子 \(n\) 放到生成函数的式子里就要对其做微分 :
然后考虑如何拼出来我们要求的平方和序列的生成函数 :
\[\large
x^2 G(x)^{\prime\prime} + x G(x)^{\prime} = \sum_{n = 0}^{\infty} sq_n x^n
\]
引入 (选修2就有的) 等比数列求和公式 :
\[\large
\sum_{i = 0}^{n} x^i = 1 + x + x^2 + x^3 + \cdots + x^n = \frac{x^{n + 1} - 1}{x - 1}
\]
对其进行两次微分,得到 :
\[\large\begin{aligned}
&1^2 + 2^2 x + 3^2 x^2 + \cdots + n^2 x^{n - 1}\\
&= \frac{n^2x^{n + 2} - (2n^2 + 2n - 1)x^{n + 1} + (n + 1)^2 x^{n} - x - 1}{(x - 1)^3}
\end{aligned}\]
两侧同乘 \(x\) :
\[\large\begin{aligned}
&1^2x + 2^2 x^2 + 3^2 x^3 + \cdots + n^2 x^{n}\\
&= \frac{n^2x^{n + 3} - (2n^2 + 2n - 1)x^{n + 2} + (n + 1)^2 x^{n + 1} - x^2 - x}{(x - 1)^3}
\end{aligned}\]
可以发现,求出 \(x = 1\) 这一特殊情况后,此式子化为我们所要求的平方和,但是出现了 \(\frac{0}{0}\) 的特殊情况.
根据 (有些人天天念叨的) 洛必达法则 :
发现分子分母两个函数在点 \(1\) 附近 去心邻域 都可导并且 对于\(g(x) = (x - 1)^3\) , 有 \(g'(x) = 3(x - 1)^2 \neq 0\). 于是可以对于分子分母分别求导,连用三次洛必达 :
\[\large\begin{aligned}
&\sum_{i = 1}^{n} i^2 \\
&= \lim_{x \to 1} \frac{n^2x^{n + 3} - (2n^2 + 2n - 1)x^{n + 2} + (n + 1)^2 x^{n + 1} - x^2 - x}{(x - 1)^3}\\
& \xlongequal{L'H} \frac{n^2(n + 3)x^{n + 2} - (n + 2)(2n^2 + 2n - 1)x^{n + 1} +(n + 1)^3 x^n - 2x - 1 }{3(x - 1)^2} \\
& \xlongequal{L'H} \frac{n^2(n + 3)(n + 2)x^{n + 1} - (n + 2)(n + 1)(2n^2 + 2n - 1)x^{n} + n(n + 1)^3 x^{n - 1} - 2 }{6(x - 1)} \\
& \xlongequal{L'H} \frac{1}{6} (n^2(n + 3)(n + 2)(n + 1)x^{n} - n(n + 1)(n + 2)(2n^2 + 2n - 1)x^{n - 1} + (n - 1)n(n + 1)^3 x^{n - 2}) \\
& = \frac{1}{6} (n^2(n + 3)(n + 2)(n + 1) - n(n + 1)(n + 2)(2n^2 + 2n - 1) + (n - 1)n(n + 1)^3) \\
& = \frac{n(n + 1)(2n + 1)}{6}\\
\end{aligned}\]
奇技淫巧
为什么把下列的内容称作奇技淫巧呢?
因为其 不可推广 或者 难以想到.
难以想到和难以理解是不同的,想到是在没有解这个问题的实际经历时找到做法,理解是对于一个做法懂得做的过程,但是可能你是在解出问题后再以上帝视角理解的.
#1
构造性证明
构造性/非构造性证明都和开脑洞似的...
看看平方和数列英文名 : Square Pyramidal Numbers .
直译就是 "方形金字塔数"
是因为这些数是很多能堆在一起形成一个 \(n\) 层金字塔的数的和.
金字塔啥样,下面这样 :
\[\large\begin{aligned}
&1\\
&2\,2\\
&3\,3\,3\\
&4\,4\,4\,4\\
&\vdots\\
&n\,n\,n\,\cdots n
\end{aligned}\]
考虑从中间对齐的话,这是一个等边三角形.
不想排版了,凑合看吧.
翻转一下 :
\[\large\begin{aligned}
&n\\
&n\,n - 1\\
&n\,n - 1\,n - 2\\
&n\,n - 1\,n - 2\,n - 3\\
&\vdots\\
&n\,n - 1\,n - 2\,\cdots 1
\end{aligned}\]
再转一下 :
\[\large\begin{aligned}
&n\\
&n - 1\,n\\
&n - 2\,n - 1\,n\\
&n - 3\,n - 2\,n - 1\,n\\
&\vdots\\
&1\,2\,3\,\cdots n
\end{aligned}\]
然后把三个三角形加起来得到的就是 \(3sq_n\) ,每个位置的和都是 \(2n + 1\) ,每个三角形有 \(\frac{n(n + 1)}{2}\) 个数,于是有 :
\[\large
3sq_n = \frac{n(n + 1)(2n + 1)}{2}
\]
#2
来自 Youtube 频道 Think Twice 的形象化证明 :
链接
想必正常人类的空间想象力不足以立即想出这种证明...
或者说我太菜了才想不出来...
#3
阿尔哈曾公式
就是那个专业对口了.
公式原型 :
\[\large
\sum_{i = 1}^{n} i^{k + 1} = (n + 1)\sum_{i = 1}^{n} i^k - \sum_{i = 1}^{n}\sum_{j = 1}^{i} j^k
\]
分别代入 \(k = 0\) 与 \(k = 1\) 即可...
#4
物理方法...
我物理拉跨,那就看看别人怎么证明的吧.
知乎@wonderwind
总结
后来去翻知乎回答,发现有一位小学老师的回答都有补充裂项求和法了,小学就有有限微积分,小学生恐怖如斯...
越到后面的方法就有越多复杂的概念,但是求解也更快(大嘘),总之,用高级知识解决低级问题就是 降维打击.
但是 OI 中更多体现的是使用数学将求值的复杂度降低到期望范围内,例如有了 \(\mathrm{O}(k^3 \log n)\) 的矩乘优化递推有些时候就没必要做生成函数求通项了.
暴力
暴力真好啊(感慨).
首先大胆猜一个结论.
看平方数的通项 : \(f_n = n^2\) , 是二次的.
通项是 \(n\) 次,大胆猜测这个数列前缀和的通项是 \(n + 1\) 次的一个多项式.
代几个值然后大力消元.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号