树链剖分,LCT学习总结
概念:
对于一棵有根树,每个非叶节点选择至多一个连向孩子的边称为 “实边”(重边) ,这个边集称为这棵树的一个链剖分,不在集合中的边称为“虚边“(轻边)。如图,黑边为重边,白边为轻边。
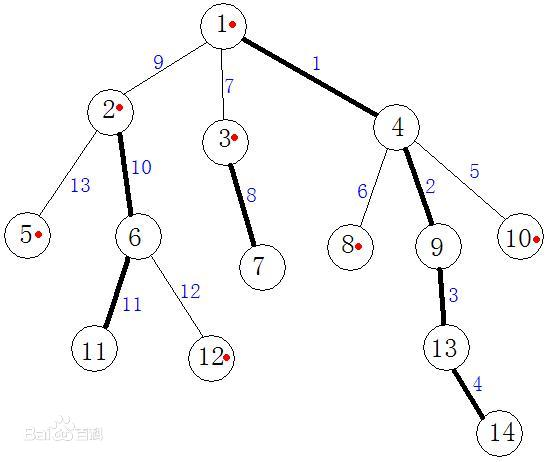
重链:
每个非叶节点向他的节点数最大的子节点连一条重边;
重链求LCA:
如果两个点在同一条链上,则深度小的为答案。否则让较深的点爬到他所在的这条重链的最高点的父亲。
【洛谷P3379】最近公共祖先(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 1000010; 8 9 int n, m; 10 int size1[N], fa[N], dep[N]; 11 int tidnum; 12 int dfn[N * 4], son[N * 4], top[N * 4], pos[N * 4]; 13 int h[N], num[N], nex[N], dqx; 14 15 void add(int a, int b) 16 { 17 num[dqx] = b; 18 nex[dqx] = h[a]; 19 h[a] = dqx++; 20 } 21 22 void dfs1(int u, int fath) 23 { 24 fa[u] = fath; 25 size1[u] = 1; 26 dep[u] = dep[fath] + 1; 27 for (int i = h[u]; ~i; i = nex[i]) 28 { 29 int j = num[i]; 30 if (j == fath) continue; 31 dfs1(j, u); 32 size1[u] += size1[j]; 33 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 34 } 35 } 36 37 void dfs2(int u, int tp) 38 { 39 dfn[u] = ++tidnum; 40 pos[dfn[u]] = u; 41 top[u] = tp; 42 43 if (!son[u]) return; 44 45 dfs2(son[u], tp); 46 for (int i = h[u]; ~i; i = nex[i]) 47 { 48 int j = num[i]; 49 if (j == son[u] || j == fa[u]) continue; 50 dfs2(j, j); 51 } 52 } 53 54 int LCA(int a, int b) 55 { 56 while (true) 57 { 58 if (dep[top[a]] < dep[top[b]]) swap(a, b); 59 if (top[a] == top[b]) return dep[a] < dep[b] ? a : b; 60 a = fa[top[a]]; 61 } 62 } 63 64 int main() 65 { 66 int s; 67 scanf("%d%d%d", &n, &m, &s); 68 69 memset(h, -1, sizeof(h)); 70 for (int i = 1; i < n; i++) 71 { 72 int a, b; 73 scanf("%d%d", &a, &b); 74 add(a, b), add(b, a); 75 } 76 dfs1(s, 0); 77 dfs2(s, s); 78 while (m--) 79 { 80 int a, b; 81 scanf("%d%d", &a, &b); 82 printf("%d\n", LCA(a, b)); 83 } 84 }
重链DFS序列:
当初始化每个节点的子节点数后(第一次DFS),再进行一次DFS,这一次DFS当递归到某一节点时,给他赋值一个下标,之后先递归他的子节点数最多的子节点,再递归其他子节点,这样就能让任意一条重链对应一个连续的区间,之后再用线段树或树状数组等数据结构维护值域。
【ZJOI2008】树的统计(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 100010; 8 9 int n; 10 int size1[N], fa[N], dep[N], son[N]; 11 int dfn[N], pos[N], top[N], dfnnum; 12 int h[N], num[N << 1], nex[N << 1], dqx; 13 14 struct Node 15 { 16 int sum, max; 17 }; 18 19 Node t[N << 2]; 20 21 void add(int a, int b) 22 { 23 num[dqx] = b; 24 nex[dqx] = h[a]; 25 h[a] = dqx++; 26 } 27 28 void dfs1(int u, int fath, int depth) 29 { 30 size1[u] = 1; 31 fa[u] = fath; 32 dep[u] = depth + 1; 33 34 for (int i = h[u]; ~i; i = nex[i]) 35 { 36 int j = num[i]; 37 if (j == fath) continue; 38 39 dfs1(j, u, depth + 1); 40 size1[u] += size1[j]; 41 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 42 } 43 } 44 45 void dfs2(int u, int tp) 46 { 47 dfn[u] = ++dfnnum; 48 pos[dfn[u]] = u; 49 top[u] = tp; 50 51 if (!son[u]) return ; 52 53 dfs2(son[u], tp); 54 55 for (int i = h[u]; ~i; i = nex[i]) 56 { 57 int j = num[i]; 58 if (j == son[u] || j == fa[u]) continue; 59 60 dfs2(j, j); 61 } 62 } 63 64 void pushup(int q) 65 { 66 t[q].max = -1e9; 67 t[q].sum = t[q << 1].sum + t[q << 1 | 1].sum; 68 t[q].max = max(t[q << 1].max, t[q << 1 | 1].max); 69 } 70 71 void modify(int q, int l, int r, int x, int v) 72 { 73 if (l == r) 74 { 75 t[q].sum = t[q].max = v; 76 return; 77 } 78 79 int mid = (l + r) >> 1; 80 if (x <= mid) modify(q << 1, l, mid, x, v); 81 if (x > mid) modify(q << 1 | 1, mid + 1, r, x, v); 82 pushup(q); 83 } 84 85 int query_sum(int q, int l, int r, int L, int R) 86 { 87 if (L <= l && r <= R) 88 { 89 return t[q].sum; 90 } 91 92 int sum = 0; 93 int mid = (l + r) >> 1; 94 if (L <= mid) sum = query_sum(q << 1, l, mid, L, R); 95 if (R > mid) sum += query_sum(q << 1 | 1, mid + 1, r, L, R); 96 return sum; 97 } 98 99 int LCA_sum(int a, int b) 100 { 101 int sum = 0; 102 while (top[a] != top[b]) 103 { 104 if (dep[top[a]] < dep[top[b]]) swap(a, b); 105 106 sum += query_sum(1, 1, n, dfn[top[a]], dfn[a]); 107 a = fa[top[a]]; 108 } 109 if (dfn[a] > dfn[b]) swap(a, b); 110 sum += query_sum(1, 1, n, dfn[a], dfn[b]); 111 return sum; 112 } 113 114 int query_max(int q, int l, int r, int L, int R) 115 { 116 if (L <= l && r <= R) 117 { 118 return t[q].max; 119 } 120 121 int sum = -1e9; 122 int mid = (l + r) >> 1; 123 if (L <= mid) sum = query_max(q << 1, l, mid, L, R); 124 if (R > mid) sum = max(sum, query_max(q << 1 | 1, mid + 1, r, L, R)); 125 return sum; 126 } 127 128 int LCA_max(int a, int b) 129 { 130 int sum = -1e9; 131 while (top[a] != top[b]) 132 { 133 if (dep[top[a]] < dep[top[b]]) swap(a, b); 134 135 sum = max(sum, query_max(1, 1, n, dfn[top[a]], dfn[a])); 136 a = fa[top[a]]; 137 } 138 if (dfn[a] > dfn[b]) swap(a, b); 139 sum = max(sum, query_max(1, 1, n, dfn[a], dfn[b])); 140 return sum; 141 } 142 143 int main() 144 { 145 scanf("%d", &n); 146 147 memset(h, -1, sizeof(h)); 148 for (int i = 1; i < n; i++) 149 { 150 int a, b; 151 scanf("%d%d", &a, &b); 152 add(a, b), add(b, a); 153 } 154 155 dfs1(1, 0, 1); 156 dfs2(1, 1); 157 158 for (int i = 1; i <= n; i++) 159 { 160 int x; 161 scanf("%d", &x); 162 modify(1, 1, n, dfn[i], x); 163 } 164 165 int q; 166 scanf("%d", &q); 167 while (q--) 168 { 169 int a, b; 170 char op[10]; 171 scanf("%s%d%d", op, &a, &b); 172 if (op[0] == 'C') 173 { 174 modify(1,1,n,dfn[a],b); 175 } 176 else 177 { 178 if (op[1] == 'M') printf("%d\n", LCA_max(a, b)); 179 else printf("%d\n", LCA_sum(a, b)); 180 } 181 } 182 }
【NOI2015】软件包管理器(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 200010; 8 9 int n; 10 int tid[N], top[N], pos[N], tidnum; 11 int size1[N], fa[N], dep[N], son[N]; 12 int h[N], nex[N * 2], num[N * 2], dqx; 13 14 struct Node 15 { 16 int l, r, sum, flag; 17 Node() {} 18 }; 19 20 Node tree[N * 4]; 21 22 void add(int a, int b) 23 { 24 num[dqx] = b; 25 nex[dqx] = h[a]; 26 h[a] = dqx++; 27 } 28 29 void dfs1(int u, int father, int depth) 30 { 31 size1[u] = 1; 32 fa[u] = father; 33 dep[u] = depth + 1; 34 for (int i = h[u]; ~i; i = nex[i]) 35 { 36 int j = num[i]; 37 if (j == father) continue; 38 dfs1(j, u, depth + 1); 39 size1[u] += size1[j]; 40 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 41 } 42 } 43 44 void dfs2(int u, int tp) 45 { 46 tid[u] = ++tidnum; 47 pos[tid[u]] = u; 48 top[u] = tp; 49 50 if (!son[u]) return; 51 52 dfs2(son[u], tp); 53 for (int i = h[u]; ~i; i = nex[i]) 54 { 55 int j = num[i]; 56 if (j != son[u] && j != fa[u]) 57 { 58 dfs2(j, j); 59 } 60 } 61 } 62 63 void build(int id, int l, int r) 64 { 65 tree[id].l = l; 66 tree[id].r = r; 67 tree[id].sum = 0; 68 tree[id].flag = -1; 69 70 if (l == r) return; 71 int mid = (l + r) >> 1; 72 build(id << 1, l, mid); 73 build(id << 1 | 1, mid + 1, r); 74 } 75 76 void pushdown(int q) 77 { 78 tree[q << 1].sum = (tree[q << 1].r - tree[q << 1].l + 1) * tree[q].flag; 79 tree[q << 1 | 1].sum = (tree[q << 1 | 1].r - tree[q << 1 | 1].l + 1) * tree[q].flag; 80 tree[q << 1].flag = tree[q << 1 | 1].flag = tree[q].flag; 81 tree[q].flag = -1; 82 } 83 84 int get(int q, int l, int r) 85 { 86 if (tree[q].r<l || tree[q].l>r) return 0; 87 if (tree[q].l >= l && tree[q].r <= r) return tree[q].sum; 88 if (~tree[q].flag) pushdown(q); 89 return get(q << 1, l, r) + get(q << 1 | 1, l, r); 90 } 91 92 void update(int q, int l, int r, int v) 93 { 94 if (tree[q].r<l || tree[q].l>r) return; 95 if (tree[q].l >= l && tree[q].r <= r) 96 { 97 tree[q].sum = (tree[q].r - tree[q].l + 1) * v; 98 tree[q].flag = v; 99 return; 100 } 101 102 if (~tree[q].flag) pushdown(q); 103 update(q << 1, l, r, v); 104 update(q << 1 | 1, l, r, v); 105 tree[q].sum = tree[q << 1].sum + tree[q << 1 | 1].sum; 106 return; 107 } 108 109 void change(int a, int b, int v) 110 { 111 while (top[a] != top[b]) 112 { 113 if (dep[a] < dep[b]) swap(a, b); 114 update(1, tid[top[a]], tid[a], v); 115 a = fa[top[a]]; 116 } 117 118 if (dep[a] > dep[b]) swap(a, b); 119 update(1, tid[a], tid[b], v); 120 return; 121 } 122 123 int main() 124 { 125 scanf("%d", &n); 126 127 memset(h, -1, sizeof(h)); 128 for (int i = 2; i <= n; i++) 129 { 130 int a; 131 scanf("%d", &a); 132 a++; 133 add(a, i); 134 } 135 136 dfs1(1, 1, 1); 137 dfs2(1, 1); 138 139 int q; 140 scanf("%d", &q); 141 build(1, 1, tidnum); 142 while (q--) 143 { 144 char s[20]; 145 scanf("%s", s); 146 147 int x; 148 scanf("%d", &x); 149 x++; 150 151 int t1 = tree[1].sum; 152 if (s[0] == 'i') 153 { 154 change(1, x, 1); 155 int t2 = tree[1].sum; 156 printf("%d\n", abs(t1 - t2)); 157 } 158 else 159 { 160 update(1, tid[x], tid[x] + size1[x] - 1, 0); 161 int t2 = tree[1].sum; 162 printf("%d\n", abs(t1 - t2)); 163 } 164 } 165 166 167 }
【HAOI2015】树上操作(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 8 const int N = 1e5 + 1; 9 10 typedef long long ll; 11 12 ll n, m; 13 ll fa[N], top[N], siz[N], son[N]; 14 ll o[N], las, p[N], v[N]; 15 bool vis[N]; 16 17 struct node 18 { 19 ll l, r, sum, tag; 20 ll len() 21 { 22 return r - l + 1; 23 } 24 }; 25 26 node tree[4 * N]; 27 28 vector<ll> g[N]; 29 30 void dfs1(ll x, ll fat, ll len) 31 { 32 fa[x] = fat; 33 siz[x] = 1; 34 for (ll i = 0; i < g[x].size(); ++i) 35 { 36 ll y = g[x][i]; 37 if (y == fat) 38 continue; 39 dfs1(y, x, len + 1); 40 siz[x] += siz[y]; 41 if (siz[y] > siz[son[x]]) 42 son[x] = y; 43 } 44 } 45 46 void dfs2(ll x, ll dp) 47 { 48 top[x] = dp; 49 o[++las] = v[x]; 50 p[x] = las; 51 if (son[x] == 0) 52 return; 53 dfs2(son[x], dp); 54 for (ll i = 0; i < g[x].size(); ++i) 55 { 56 ll y = g[x][i]; 57 if (y == fa[x] || y == son[x]) 58 continue; 59 dfs2(y, y); 60 } 61 } 62 63 64 void build(ll l, ll r, ll k) 65 { 66 tree[k].l = l; 67 tree[k].r = r; 68 if (l == r) 69 { 70 tree[k].sum = o[l]; 71 return; 72 } 73 ll mid = (l + r) / 2; 74 build(l, mid, 2 * k); 75 build(mid + 1, r, 2 * k + 1); 76 tree[k].sum = tree[2 * k].sum + tree[2 * k + 1].sum; 77 } 78 79 void but(ll k, ll tag) 80 { 81 tree[k].sum += tree[k].len() * tag; 82 tree[k].tag += tag; 83 } 84 85 void pushdown(ll k) 86 { 87 but(2 * k, tree[k].tag); 88 but(2 * k + 1, tree[k].tag); 89 tree[k].tag = 0; 90 } 91 92 void update(ll x, ll y, ll a, ll k) 93 { 94 ll l = tree[k].l, r = tree[k].r; 95 if (x <= l && y >= r) 96 { 97 but(k, a); 98 return; 99 } 100 101 if (tree[k].tag) pushdown(k); 102 ll mid = (l + r) / 2; 103 if (x <= mid) update(x, y, a, 2 * k); 104 if (y >= mid + 1) update(x, y, a, 2 * k + 1); 105 tree[k].sum = tree[2 * k].sum + tree[2 * k + 1].sum; 106 } 107 108 ll query(ll x, ll y, ll k) 109 { 110 ll l = tree[k].l, r = tree[k].r; 111 112 if (x <= l && y >= r) return tree[k].sum; 113 114 if (tree[k].tag) pushdown(k); 115 116 ll mid = (l + r) / 2, ans = 0; 117 if (x <= mid) ans += query(x, y, 2 * k); 118 if (y >= mid + 1) ans += query(x, y, 2 * k + 1); 119 return ans; 120 } 121 122 int main() 123 { 124 scanf("%lld%lld", &n, &m); 125 126 for (ll i = 1; i <= n; ++i) scanf("%lld", &v[i]); 127 for (ll i = 1; i <= n - 1; ++i) 128 { 129 ll a, b; 130 scanf("%lld%lld", &a, &b); 131 g[a].push_back(b); 132 g[b].push_back(a); 133 } 134 135 dfs1(1, 0, 1); 136 dfs2(1, 1); 137 build(1, n, 1); 138 139 for (ll i = 1; i <= m; ++i) 140 { 141 ll cmd, x, a; 142 scanf("%lld%lld", &cmd,&x); 143 144 if (cmd == 1) 145 { 146 scanf("%lld", &a); 147 update(p[x], p[x], a, 1); 148 } 149 if (cmd == 2) 150 { 151 scanf("%lld", &a); 152 update(p[x], p[x] + siz[x] - 1, a, 1); 153 } 154 if (cmd == 3) 155 { 156 ll sum = 0; 157 while (top[x] != 1) 158 { 159 sum += query(p[top[x]], p[x], 1); 160 x = fa[top[x]]; 161 } 162 sum += query(1, p[x], 1); 163 printf("%lld\n", sum); 164 } 165 } 166 }
【洛谷 P3384】轻重链剖分(题目):
模板
 View Code
View Code
【JLOI2014】松鼠的新家(题目):
按照参观顺序,其实就是树上的路径a1~a2,a2~a3,a3~a4……an-1~an上的节点权值都加一,故用树链剖分和线段树维护,注意路径a~b上的点权值都加一后,要把b节点的权值再减一,因为下一次计算会重复,而且最后一个参观的房子不用放糖。
ps: 要在函数前加inline才能卡过去,不然有一个点莫名超时。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 #define ls(q) q<<1 8 #define rs(q) q<<1|1 9 10 const int N = 600010; 11 12 int n; 13 int s[N]; 14 int t[N * 4], tot; 15 int size1[N], dfn[N], son[N], fa[N], dep[N], dfnnum; 16 int pos[N * 4], flag[N * 4], top[N * 4]; 17 int h[N], num[N], nex[N], dqx; 18 19 inline void add(int a, int b) 20 { 21 num[dqx] = b; 22 nex[dqx] = h[a]; 23 h[a] = dqx++; 24 } 25 26 inline void dfs1(int u, int fath) 27 { 28 size1[u] = 1; 29 fa[u] = fath; 30 dep[u] = dep[fath] + 1; 31 32 for (int i = h[u]; ~i; i = nex[i]) 33 { 34 int j = num[i]; 35 if (j == fath) continue; 36 dfs1(j, u); 37 size1[u] += size1[j]; 38 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 39 } 40 } 41 42 inline void dfs2(int u, int tp) 43 { 44 dfn[u] = ++dfnnum; 45 pos[dfn[u]] = u; 46 top[u] = tp; 47 48 if (!son[u]) return; 49 50 dfs2(son[u], tp); 51 52 for (int i = h[u]; ~i; i = nex[i]) 53 { 54 int j = num[i]; 55 if (j == fa[u] || j == son[u]) continue; 56 dfs2(j, j); 57 } 58 } 59 60 inline void pushdown(int q, int l, int r) 61 { 62 if (!flag[q]) return; 63 64 int mid = (l + r) >> 1; 65 t[ls(q)] += flag[q] * (mid - l + 1); 66 flag[ls(q)] += flag[q]; 67 68 t[rs(q)] += flag[q] * (r - mid); 69 flag[rs(q)] += flag[q]; 70 71 flag[q] = 0; 72 } 73 74 inline void insert(int q, int l, int r, int L, int R, int v) 75 { 76 if (L <= l && r <= R) 77 { 78 t[q] += v; 79 flag[q] += v; 80 return; 81 } 82 83 pushdown(q, l, r); 84 int mid = (l + r) >> 1; 85 if (L <= mid) insert(ls(q), l, mid, L, R, v); 86 if (R > mid) insert(rs(q), mid + 1, r, L, R, v); 87 } 88 89 inline int query(int q, int l, int r, int x) 90 { 91 if (l == r) 92 { 93 return t[q]; 94 } 95 96 pushdown(q, l, r); 97 int mid = (l + r) >> 1; 98 if (x <= mid) return query(ls(q), l, mid, x); 99 else return query(rs(q), mid + 1, r, x); 100 } 101 102 inline void update(int a, int b, int v) 103 { 104 while (true) 105 { 106 if (dep[top[a]] < dep[top[b]]) swap(a, b); 107 if (top[a] == top[b]) 108 { 109 if (dfn[a] > dfn[b]) swap(a, b); 110 insert(1, 1, n, dfn[a], dfn[b], v); 111 return; 112 } 113 insert(1, 1, n, dfn[top[a]], dfn[a], v); 114 a = fa[top[a]]; 115 } 116 } 117 118 int main() 119 { 120 scanf("%d", &n); 121 for (int i = 1; i <= n; i++) 122 { 123 scanf("%d", &s[i]); 124 } 125 126 memset(h, -1, sizeof(h)); 127 for (int i = 1; i < n; i++) 128 { 129 int a, b; 130 scanf("%d%d", &a, &b); 131 add(a, b), add(b, a); 132 } 133 134 dfs1(s[1], 0); 135 dfs2(s[1], s[1]); 136 137 for (int i = 1; i < n; i++) 138 { 139 int a = s[i], b = s[i + 1]; 140 update(a, b, 1); 141 update(b, b, -1); 142 } 143 for (int i = 1; i <= n; i++) 144 { 145 printf("%d\n", query(1, 1, n, dfn[i])); 146 } 147 }
【SDOI2011】染色(题目):
线段树维护树上的操作,线段树合并时判断两个节点的衔接处的颜色是否一样,不一样合并后的节点的颜色段数就为两个子节点的段数和,否则为段数和和-1

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 typedef long long LL; 8 9 const int N = 100010; 10 11 int n, m; 12 int cnt, Lc, Rc; 13 int col[N], sz[N], dep[N]; 14 int fa[N], son[N], top[N], pos[N]; 15 int dqx, h[N], num[N << 1], nex[N << 1]; 16 char str[50]; 17 18 struct node 19 { 20 int l, r; 21 int num, tag, lc, rc; 22 }t[N << 2]; 23 24 void add(int a, int b) 25 { 26 num[dqx] = b; 27 nex[dqx] = h[a]; 28 h[a] = dqx++; 29 } 30 31 void dfs1(int u, int fath, int depth) 32 { 33 sz[u] = 1; 34 fa[u] = fath; 35 son[u] = 0; 36 dep[u] = depth; 37 for (int i = h[u]; i != -1; i = nex[i]) 38 { 39 int j = num[i]; 40 if (j == fath) continue; 41 42 dfs1(j, u, depth + 1); 43 sz[u] += sz[j]; 44 if (sz[son[u]] < sz[j]) son[u] = j; 45 } 46 } 47 48 void dfs2(int u, int tp) 49 { 50 pos[u] = ++cnt; 51 top[u] = tp; 52 if (son[u] != 0) dfs2(son[u], top[u]); 53 for (int i = h[u]; i != -1; i = nex[i]) 54 { 55 int j = num[i]; 56 if (j == fa[u] || j == son[u]) continue; 57 dfs2(j, j); 58 } 59 } 60 61 void push_down(int q) 62 { 63 if (t[q].tag) 64 { 65 t[q << 1].tag = t[q << 1 | 1].tag = t[q].tag; 66 t[q << 1].num = t[q << 1 | 1].num = 1; 67 t[q << 1].lc = t[q << 1].rc = t[q].lc; 68 t[q << 1 | 1].lc = t[q << 1 | 1].rc = t[q].lc; 69 t[q].tag = 0; 70 } 71 } 72 73 void push_up(int q) 74 { 75 t[q].lc = t[q<<1].lc; 76 t[q].rc = t[q << 1|1].rc; 77 78 int ans = t[q << 1].num + t[q << 1 | 1].num; 79 if (t[q << 1].rc == t[q << 1 | 1].lc) ans--; 80 t[q].num = ans; 81 } 82 83 void build(int q, int l, int r) 84 { 85 t[q].l = l; 86 t[q].r = r; 87 t[q].num = 0; 88 if (l == r) return; 89 90 int mid = (l + r) >> 1; 91 build(q << 1, l, mid); build(q << 1 | 1, mid + 1, r); 92 } 93 94 void update(int q, int l, int r, int x) 95 { 96 if (t[q].l == l && t[q].r == r) 97 { 98 t[q].num = t[q].tag = 1; 99 t[q].lc = t[q].rc = x; 100 return; 101 } 102 103 push_down(q); 104 int mid = (t[q].l + t[q].r) >> 1; 105 if (r <= mid) update(q<<1, l, r, x); 106 else if (l > mid) update(q << 1 | 1, l, r, x); 107 else 108 { 109 update(q << 1, l, mid, x); 110 update(q<<1|1, mid + 1, r, x); 111 } 112 push_up(q); 113 } 114 115 int query(int q, int l, int r, int L, int R) 116 { 117 if (t[q].l == L) Lc = t[q].lc; 118 if (t[q].r == R) Rc = t[q].rc; 119 if (t[q].l == l && t[q].r == r) return t[q].num; 120 121 push_down(q); 122 int mid = (t[q].l + t[q].r) >> 1; 123 if (r <= mid) return query(q << 1, l, r, L, R); 124 else if (l > mid) return query(q << 1 | 1, l, r, L, R); 125 else 126 { 127 int ans = query(q << 1, l, mid, L, R) + query(q << 1 | 1, mid + 1, r, L, R); 128 if (t[q << 1].rc == t[q << 1 | 1].lc) ans--; 129 return ans; 130 } 131 push_up(q); 132 } 133 134 int solve(int u, int v, int id, int c) 135 { 136 int ans = 0; 137 if (id == 1) 138 { 139 while (top[u] != top[v]) 140 { 141 if (dep[top[u]] < dep[top[v]]) swap(u, v); 142 update(1, pos[top[u]], pos[u], c); 143 u = fa[top[u]]; 144 } 145 146 if (dep[u] > dep[v]) swap(u, v); 147 update(1, pos[u], pos[v], c); 148 } 149 else 150 { 151 int ans1 = -1, ans2 = -1; 152 while (top[u] != top[v]) 153 { 154 if (dep[top[u]] < dep[top[v]]) 155 { 156 swap(u, v); swap(ans1, ans2); 157 } 158 159 ans += query(1, pos[top[u]], pos[u], pos[top[u]], pos[u]); 160 if (Rc == ans1) ans--; 161 ans1 = Lc; u = fa[top[u]]; 162 } 163 164 if (dep[u] < dep[v]) 165 { 166 swap(u, v); 167 swap(ans1, ans2); 168 } 169 170 ans += query(1, pos[v], pos[u], pos[v], pos[u]); 171 if (Rc == ans1) ans--; 172 if (Lc == ans2) ans--; 173 } 174 return ans; 175 } 176 177 int main() 178 { 179 scanf("%d%d", &n, &m); 180 for (int i = 1; i <= n; i++) scanf("%d", &col[i]); 181 182 memset(h, -1, sizeof(h)); 183 for (int i = 1; i < n; i++) 184 { 185 int a, b; 186 scanf("%d%d", &a, &b); 187 add(a, b); 188 add(b, a); 189 } 190 191 dfs1(1, 1, 1); 192 dfs2(1, 1); 193 build(1, 1, n); 194 195 for (int i = 1; i <= n; i++) update(1, pos[i], pos[i], col[i]); 196 197 while (m--) 198 { 199 scanf("%s", str); 200 int u, v; 201 if (str[0] == 'C') 202 { 203 int c; 204 scanf("%d%d%d", &u, &v, &c); 205 solve(u, v, 1, c); 206 } 207 else 208 { 209 int u, v; 210 scanf("%d%d", &u, &v); 211 printf("%d\n", solve(u, v, 2, 0)); 212 } 213 } 214 }
【SDOI2014】旅行(题目):
每种信仰建一个线段树,每个线段树分别维护区间和和最大值两个值,询问时只查询起点城市的信仰种类的线段树
ps:节点太多 要动态开点

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 100010; 8 9 int n; 10 int rat[N], fai[N]; 11 int size1[N], fa[N], dep[N]; 12 int root[N], lc[N << 4], rc[N << 4], tot; 13 int dfn[N], pos[N], top[N], son[N], dfnnum; 14 int h[N], num[N << 1], nex[N << 1], dqx; 15 16 struct Node 17 { 18 int sum, ma; 19 }; 20 21 Node t[N << 4]; 22 23 void add(int a, int b) 24 { 25 num[dqx] = b; 26 nex[dqx] = h[a]; 27 h[a] = dqx++; 28 } 29 30 void dfs1(int u, int fath, int depth) 31 { 32 size1[u] = 1; 33 fa[u] = fath; 34 dep[u] = depth; 35 for (int i = h[u]; ~i; i = nex[i]) 36 { 37 int j = num[i]; 38 if (j == fath) continue; 39 40 dfs1(j, u, depth + 1); 41 size1[u] += size1[j]; 42 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 43 } 44 } 45 46 void dfs2(int u, int tp) 47 { 48 dfn[u] = ++dfnnum; 49 pos[dfn[u]] = u; 50 top[u] = tp; 51 52 if (son[u]) 53 { 54 dfs2(son[u], tp); 55 } 56 57 for (int i = h[u]; ~i; i = nex[i]) 58 { 59 int j = num[i]; 60 if (j == fa[u] || j == son[u]) continue; 61 62 dfs2(j, j); 63 } 64 } 65 66 void pushup(int q) 67 { 68 t[q].sum = t[lc[q]].sum + t[rc[q]].sum; 69 t[q].ma = max(t[lc[q]].ma, t[rc[q]].ma); 70 } 71 72 void modify(int& q, int l, int r, int x, int v) 73 { 74 if (!q) q = ++tot; 75 if (l == r) 76 { 77 t[q].sum = t[q].ma = v; 78 return; 79 } 80 81 int mid = (l + r) >> 1; 82 if (x <= mid) modify(lc[q], l, mid, x, v); 83 if (x > mid) modify(rc[q], mid + 1, r, x, v); 84 pushup(q); 85 } 86 87 int query_sum(int q, int l, int r, int L, int R) 88 { 89 if (!q) return 0; 90 if (L <= l && r <= R) 91 { 92 return t[q].sum; 93 } 94 95 int res = 0; 96 int mid = (l + r) >> 1; 97 if (L <= mid) res = query_sum(lc[q], l, mid, L, R); 98 if (mid < R) res += query_sum(rc[q], mid + 1, r, L, R); 99 return res; 100 } 101 102 int query_max(int q, int l, int r, int L, int R) 103 { 104 if (!q) return 0; 105 if (L <= l && r <= R) 106 { 107 return t[q].ma; 108 } 109 110 int res = 0; 111 int mid = (l + r) >> 1; 112 if (L <= mid) res = max(res, query_max(lc[q], l, mid, L, R)); 113 if (mid < R) res = max(res, query_max(rc[q], mid + 1, r, L, R)); 114 return res; 115 } 116 117 int LCA_sum(int a, int b) 118 { 119 int sum = 0; 120 int root1 = root[fai[a]]; 121 while (top[a] != top[b]) 122 { 123 if (dep[top[a]] < dep[top[b]]) swap(a, b); 124 sum += query_sum(root1, 1, n, dfn[top[a]], dfn[a]); 125 a = fa[top[a]]; 126 } 127 128 if (dep[a] > dep[b]) swap(a, b); 129 sum += query_sum(root1, 1, n, dfn[a], dfn[b]); 130 return sum; 131 } 132 133 int LCA_max(int a, int b) 134 { 135 int sum = 0; 136 int root1 = root[fai[a]]; 137 while (top[a] != top[b]) 138 { 139 if (dep[top[a]] < dep[top[b]]) swap(a, b); 140 sum = max(sum, query_max(root1, 1, n, dfn[top[a]], dfn[a])); 141 a = fa[top[a]]; 142 } 143 144 if (dep[a] > dep[b]) swap(a, b); 145 sum = max(sum, query_max(root1, 1, n, dfn[a], dfn[b])); 146 return sum; 147 } 148 149 int main() 150 { 151 int Q; 152 scanf("%d%d", &n, &Q); 153 for (int i = 1; i <= n; i++) scanf("%d%d", &rat[i], &fai[i]); 154 155 memset(h, -1, sizeof(h)); 156 for (int i = 1; i < n; i++) 157 { 158 int a, b; 159 scanf("%d%d", &a, &b); 160 add(a, b), add(b, a); 161 } 162 163 dfs1(1, 0, 1); 164 dfs2(1, 1); 165 for (int i = 1; i <= n; i++) 166 { 167 modify(root[fai[i]], 1, n, dfn[i], rat[i]); 168 } 169 170 while (Q--) 171 { 172 char op[5]; 173 int a, b; 174 scanf("%s%d%d", op, &a, &b); 175 176 if (op[0] == 'C') 177 { 178 if (op[1] == 'C') 179 { 180 modify(root[fai[a]], 1, n, dfn[a], 0); 181 fai[a] = b; 182 modify(root[fai[a]], 1, n, dfn[a], rat[a]); 183 } 184 else 185 { 186 rat[a] = b; 187 modify(root[fai[a]], 1, n, dfn[a], rat[a]); 188 } 189 } 190 else 191 { 192 if (op[1] == 'S') 193 { 194 printf("%d\n", LCA_sum(a, b)); 195 } 196 else 197 { 198 printf("%d\n", LCA_max(a, b)); 199 } 200 } 201 } 202 }
【LNOI2014】LCA (题目):
求LCA(x,y)的深度,可以将x到根的路径上的每一个点权值加一,再将求y到根的路径上的点权值和,便是LCA(x,y)的深度了。既然如此,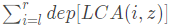 我们可以将l到r之间的点都进行一次将其到根的路径上的点的权值加一的操作,最后求z到根的路径的点权值和便是
我们可以将l到r之间的点都进行一次将其到根的路径上的点的权值加一的操作,最后求z到根的路径的点权值和便是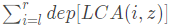 的值了。为了方便运算,先把0~l-1的所有点都进行一次操作,求得z到根的权值和f(l-1),再把l~r的点都进行一次操作求得z到根的权值和f(r),最后
的值了。为了方便运算,先把0~l-1的所有点都进行一次操作,求得z到根的权值和f(l-1),再把l~r的点都进行一次操作求得z到根的权值和f(r),最后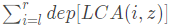 的值便是f(r)-f(l-1)。
的值便是f(r)-f(l-1)。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 2000010, mod = 201314; 8 9 int n; 10 int ans[N]; 11 int son[N], fa[N], size1[N], dep[N]; 12 int sum[N], lazy[N]; 13 int dfn[N], top[N], pos[N], dfnnum; 14 int h[N], num[N], nex[N], dqx; 15 16 struct Node 17 { 18 int id, pos, z, flag; 19 20 Node() { id = pos = z = flag = 0; } 21 Node(int id, int pos, int z, int flag) : id(id), pos(pos), z(z), flag(flag) {} 22 23 bool operator < (const Node& thr) const 24 { 25 return this->pos < thr.pos; 26 } 27 }; 28 29 Node ask[N]; 30 31 void add(int a, int b) 32 { 33 num[dqx] = b; 34 nex[dqx] = h[a]; 35 h[a] = dqx++; 36 } 37 38 void dfs1(int u, int f) 39 { 40 fa[u] = f; 41 size1[u] = 1; 42 dep[u] = dep[f] + 1; 43 44 for (int i = h[u]; ~i; i = nex[i]) 45 { 46 int j = num[i]; 47 if (j == f) continue; 48 dfs1(j, u); 49 size1[u] += size1[j]; 50 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 51 } 52 } 53 54 void dfs2(int u, int tp) 55 { 56 dfn[u] = ++dfnnum; 57 pos[dfnnum] = u; 58 top[u] = tp; 59 60 if (!son[u]) return; 61 dfs2(son[u], tp); 62 63 for (int i = h[u]; ~i; i = nex[i]) 64 { 65 int j = num[i]; 66 if (j == fa[u] || j == son[u]) continue; 67 68 dfs2(j, j); 69 } 70 } 71 72 void pushup(int q) 73 { 74 sum[q] = (sum[q << 1] + sum[q << 1 | 1]) % mod; 75 } 76 77 void pushdown(int q, int l, int r) 78 { 79 if (!lazy[q]) return; 80 81 int mid = (l + r) >> 1; 82 sum[q << 1] = (sum[q << 1] + (mid - l + 1) * lazy[q] % mod) % mod; 83 sum[q << 1 | 1] = (sum[q << 1 | 1] + (r - mid) * lazy[q] % mod) % mod; 84 lazy[q << 1] += lazy[q]; 85 lazy[q << 1 | 1] += lazy[q]; 86 lazy[q] = 0; 87 } 88 89 void update(int q, int l, int r, int L, int R) 90 { 91 if (l == L && r == R) 92 { 93 sum[q] = (sum[q] + (r - l + 1)) % mod; 94 lazy[q]++; 95 return; 96 } 97 98 pushdown(q, l, r); 99 int mid = (l + r) >> 1; 100 if (R <= mid) update(q << 1, l, mid, L, R); 101 else if (L > mid) update(q << 1 | 1, mid + 1, r, L, R); 102 else update(q << 1, l, mid, L, mid), update(q << 1 | 1, mid + 1, r, mid + 1, R); 103 pushup(q); 104 } 105 106 int query(int q, int l, int r, int L, int R) 107 { 108 if (L == l && R == r) 109 { 110 return sum[q]; 111 } 112 113 pushdown(q, l, r); 114 int mid = (l + r) >> 1; 115 if (R <= mid) return query(q << 1, l, mid, L, R); 116 else if (L > mid) return query(q << 1 | 1, mid + 1, r, L, R); 117 else return (query(q << 1, l, mid, L, mid) + query(q << 1 | 1, mid + 1, r, mid + 1, R)) % mod; 118 } 119 120 void push(int u) 121 { 122 while (top[u] != 1) 123 { 124 update(1, 1, n, dfn[top[u]], dfn[u]); 125 u = fa[top[u]]; 126 } 127 update(1, 1, n, dfn[top[u]], dfn[u]); 128 } 129 130 int get(int u) 131 { 132 int res = 0; 133 while (top[u] != 1) 134 { 135 res = (res + query(1, 1, n, dfn[top[u]], dfn[u])) % mod; 136 u = fa[top[u]]; 137 } 138 res = (res + query(1, 1, n, dfn[top[u]], dfn[u])) % mod; 139 return res; 140 } 141 142 143 int main() 144 { 145 //freopen("uot.txt", "w", stdout); 146 147 int q; 148 scanf("%d%d", &n, &q); 149 150 memset(h, -1, sizeof(h)); 151 for (int i = 2; i <= n; i++) // 为了方便 将每个节点编号加一 152 { 153 int x; 154 scanf("%d", &x); 155 x++; 156 add(i, x), add(x, i); 157 } 158 159 int cnt = 0; 160 for (int i = 1; i <= q; i++) 161 { 162 int l, r, z; 163 scanf("%d%d%d", &l, &r, &z); 164 r++, z++; // 因为最后要用f(r)-f(l-1) 所以l不用加一 165 166 ask[++cnt] = Node(i, l, z, 0); 167 ask[++cnt] = Node(i, r, z, 1); 168 } 169 sort(ask + 1, ask + 1 + cnt); 170 171 dfs1(1, 0); 172 dfs2(1, 1); 173 174 int j = 1; 175 while (ask[j].pos == 0) j++; // 注意把pos为0的ask清除,因为后边不会进行0号点 的操作 176 for (int i = 1; i <= n; i++) 177 { 178 push(i); 179 while (j <= cnt && ask[j].pos == i) 180 { 181 if (ask[j].flag) ans[ask[j].id] += get(ask[j].z); //当前这个pos是r 答案要加上 182 else ans[ask[j].id] -= get(ask[j].z); //当前这个pos是l-1 答案要减去 183 j++; 184 } 185 } 186 187 for (int i = 1; i <= q; i++) 188 { 189 printf("%d\n", (ans[i] + mod) % mod); 190 } 191 }
DSU On Tree:
如果是要解决若干个有关子树的询问,可以按照这种框架来做:
先进行重链剖分,之后对于节点x: 1、递归所有的轻孩子,每个递归返回前需要撤销递归产生的副作用 ;2、递归重孩子,并且不消除副作用 ; 3、统计所有轻孩子对答案的贡献 ;4、得到当前节点x的答案 ; 5、如果需要撤销,则撤销所有轻孩子对答案的影响。
【CF600E】 Lomsat gelral(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 typedef long long LL; 8 9 const int N = 200010; 10 11 int n; 12 LL Son, sum, Ma; 13 LL col[N], ans[N], cnt[N]; 14 LL size1[N], fa[N], son[N]; 15 int h[N], num[N], nex[N], dqx; 16 17 void add(int a, int b) 18 { 19 num[dqx] = b; 20 nex[dqx] = h[a]; 21 h[a] = dqx++; 22 } 23 24 void dfs1(LL u, LL f) 25 { 26 size1[u] = 1; 27 LL Max = 0; 28 for (int i = h[u]; ~i; i = nex[i]) 29 { 30 LL j = num[i]; 31 if (j == f) continue; 32 fa[j] = u; 33 dfs1(j, u); 34 size1[u] += size1[j]; 35 if (size1[j] > Max || !son[u]) 36 { 37 Max = size1[j]; 38 son[u] = j; 39 } 40 } 41 } 42 43 void change(LL u, LL v) 44 { 45 cnt[col[u]] += v; 46 if (cnt[col[u]] > Ma) 47 { 48 Ma = cnt[col[u]]; 49 sum = col[u]; 50 } 51 else if (cnt[col[u]] == Ma) sum += col[u]; 52 53 for (int i = h[u]; ~i; i = nex[i]) 54 { 55 LL j = num[i]; 56 if (j == fa[u] || j == Son) continue; 57 change(j, v); 58 } 59 } 60 61 void dfs2(LL u, LL pd) 62 { 63 for (int i = h[u]; ~i; i = nex[i]) 64 { 65 LL j = num[i]; 66 if (j == fa[u] || j == son[u]) continue; 67 dfs2(j, 0); 68 } 69 if (son[u]) 70 { 71 dfs2(son[u], 1); 72 Son = son[u]; 73 } 74 75 change(u, 1); 76 ans[u] = sum; 77 Son = 0; 78 if (!pd) 79 { 80 change(u, -1); 81 sum = Ma = 0; 82 } 83 } 84 85 int main() 86 { 87 scanf("%d", &n); 88 for (int i = 1; i <= n; i++) 89 { 90 scanf("%lld", &col[i]); 91 } 92 93 memset(h, -1, sizeof(h)); 94 for (int i = 1; i < n; i++) 95 { 96 int a, b; 97 scanf("%d%d", &a, &b); 98 add(a, b); 99 add(b, a); 100 } 101 102 dfs1(1, 0); 103 dfs2(1, 0); 104 for (int i = 1; i <= n; i++) printf("%lld ", ans[i]); 105 }
长链剖分:
每个非叶节点选取连向最深孩子的边作为实边
长链剖分求k级祖先:
假设已经预处理了每一个节点的2i级祖先。假设找到了询问节点的2i级祖先满足2i<k<2i+1 。求出其所在重链的节点并且按照深度列入表格。假设重链长度为d 。在预处理的时候找到每条重链的根节点的1到d级祖先,放入表格。根据长链剖分的性质,k-2i<2i<d , 可以在这条长链的表格上求出的这个节点的k级祖先。预处理倍增出2i次级祖先,同时预处理每条重链对应的表格。
长链剖分优化树上DP:
从子节点DP到根节点时,对于在与当前节点同一条长链的子节点,将子节点DP过的数据接在当前节点上(指针维护),当前节点的其他子节点则暴力合并。
【CF1009F】Dominant Indices(题目):
长链优化DP,与当前节点在同一长链的子节点与当前节点共用一个DP数组内存(子节点的DP过程直接接在当前节点上),其他子节点则暴力合并
 View Code
View Code
【POI2014】Hotels 加强版(题目):
设fi,j为满足x在i的子树中且d(x,i)= j的x的个数,gi,j为满足x,y在i的子树中且d(lca(x,y),x)=d(lca(x,y),y)=d(lca(x,y),i)+j的无序数对(x,y)的个数、
可以推出转移:
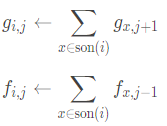
之后再用长链优化DP就行了

1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 typedef long long LL; 9 10 const int N = 100010; 11 12 int n; 13 int d[N], dep[N], son[N]; 14 int h[N], num[N << 1], nex[N << 1], dqx; 15 LL * f[N], * g[N], p[N << 2], * o = p, ans; 16 17 void add(int a, int b) 18 { 19 num[dqx] = b; 20 nex[dqx] = h[a]; 21 h[a] = dqx++; 22 } 23 24 void dfs(int u, int fa) 25 { 26 d[u] = d[fa] + 1; 27 for (int i = h[u]; ~i; i = nex[i]) 28 { 29 int j = num[i]; 30 if (j == fa) continue; 31 32 dfs(j, u); 33 if (dep[j] > dep[son[u]]) son[u] = j; 34 } 35 dep[u] = dep[son[u]] + 1; 36 } 37 38 void dp(int u, int fa) 39 { 40 if (son[u]) 41 { 42 f[son[u]] = f[u] + 1; 43 g[son[u]] = g[u] - 1; 44 dp(son[u], u); 45 } 46 47 f[u][0] = 1; 48 ans += g[u][0]; 49 for (int i = h[u]; ~i; i = nex[i]) 50 { 51 int j = num[i]; 52 if (j == fa || j == son[u]) continue; 53 54 f[j] = o; 55 o += dep[j] << 1; 56 g[j] = o; 57 o += dep[j] << 1; 58 59 dp(j, u); 60 for (int i = 0; i < dep[j]; i++) 61 { 62 if (i) ans += f[u][i - 1] * g[j][i]; 63 ans += g[u][i + 1] * f[j][i]; 64 } 65 for (int i = 0; i < dep[j]; i++) 66 { 67 g[u][i + 1] += f[u][i + 1] * f[j][i]; 68 if (i) g[u][i - 1] += g[j][i]; 69 f[u][i + 1] += f[j][i]; 70 } 71 } 72 } 73 74 int main() 75 { 76 scanf("%d", &n); 77 78 memset(h, -1, sizeof(h)); 79 for (int i = 1; i < n; i++) 80 { 81 int a, b; 82 scanf("%d%d", &a, &b); 83 add(a, b), add(b, a); 84 } 85 dfs(1, 0); 86 87 f[1] = o; 88 o += dep[1] << 1; 89 g[1] = o; 90 o += dep[1] << 1; 91 92 dp(1, 0); 93 printf("%lld", ans); 94 }
【洛谷P3899】(湖南集训)谈笑风生(题目):
设f(u,k)表示所有与u谈笑风生的v,且u是v的祖先时的答案。
可得:
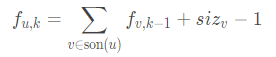
再长链剖分优化DP,最后算答案时加上当b是a的祖先时的答案。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 typedef long long LL; 8 9 const int N = 2000010; 10 11 int n; 12 LL tag[N], ans[N]; 13 int top[N], son[N], F[N]; 14 int size1[N], dep[N], undep[N]; 15 int h[N], num[N], nex[N], dqx; 16 int Q_h[N], Q_num[N], Q_id[N], Q_nex[N], qlen; 17 LL q[N]; 18 LL* f[N], * cnt = q; 19 20 struct Node 21 { 22 int u, k; 23 }; 24 25 Node que[N]; 26 27 void add(int a, int b) 28 { 29 num[dqx] = b; 30 nex[dqx] = h[a]; 31 h[a] = dqx++; 32 } 33 34 void add_query(int a, int b, int id) 35 { 36 Q_num[qlen] = b; 37 Q_id[qlen] = id; 38 Q_nex[qlen] = Q_h[a]; 39 Q_h[a] = qlen++; 40 } 41 42 void dfs1(int u, int fa) 43 { 44 F[u] = fa; 45 dep[u] = dep[fa] + 1; 46 size1[u] = 1; 47 for (int i = h[u]; ~i; i = nex[i]) 48 { 49 int j = num[i]; 50 if (j == fa) continue; 51 52 dfs1(j, u); 53 size1[u] += size1[j]; 54 if (!son[u] || undep[j] > undep[son[u]]) son[u] = j; 55 } 56 undep[u] = undep[son[u]] + 1; 57 } 58 59 void dfs2(int u, int tp) 60 { 61 top[u] = tp; 62 63 if (!son[u]) return; 64 dfs2(son[u], tp); 65 66 for (int i = h[u]; ~i; i = nex[i]) 67 { 68 int j = num[i]; 69 if (j == F[u] || j == son[u]) continue; 70 71 dfs2(j, j); 72 } 73 } 74 75 void dfs(int u) 76 { 77 if (son[u]) 78 { 79 f[son[u]] = f[u] + 1; 80 dfs(son[u]); 81 f[u][0] = 0; 82 tag[u] = tag[son[u]] + size1[son[u]] - 1; 83 } 84 85 for (int i = h[u]; ~i; i = nex[i]) 86 { 87 int j = num[i]; 88 if (j == son[u] || j == F[u]) continue; 89 90 f[j] = cnt; 91 cnt += undep[j]; 92 dfs(j); 93 tag[u] += tag[j] + size1[j] - 1; 94 95 for (int k = 1; k <= undep[j]; k++) 96 { 97 f[u][k] += f[j][k - 1]; 98 } 99 } 100 101 f[u][0] = -tag[u]; 102 for (int i = Q_h[u]; ~i; i = Q_nex[i]) 103 { 104 ans[Q_id[i]] = f[u][min(que[Q_id[i]].k, undep[u] - 1)] + tag[u]; 105 } 106 } 107 108 int main() 109 { 110 int q; 111 scanf("%d%d", &n, &q); 112 113 memset(h, -1, sizeof(h)); 114 for (int i = 1; i < n; i++) 115 { 116 int a, b; 117 scanf("%d%d", &a, &b); 118 add(a, b), add(b, a); 119 } 120 121 memset(Q_h, -1, sizeof(Q_h)); 122 for (int i = 1; i <= q; i++) 123 { 124 scanf("%d%d", &que[i].u, &que[i].k); 125 add_query(que[i].u, que[i].k, i); 126 } 127 128 dfs1(1, 0); 129 dfs2(1, 1); 130 131 f[1] = cnt; 132 cnt += undep[1]; 133 dfs(1); 134 135 for (int i = 1; i <= q; i++) 136 { 137 printf("%lld\n", ans[i] + (LL)min(dep[que[i].u] - 1, que[i].k)* (size1[que[i].u] - 1)); 138 } 139 }
PS:根据题目选择用重链还是长链
Link Cut Tree - LCT动态树
概念:
用Spaly(平衡树)维护树链剖分,对于每条实链建立一个Splay。
辅助树:
一些Splay构成了辅助树,每棵Splay维护原树中的一条路径,中序遍历一棵Splay得到的序列对应原树从上到下的一条路径。不需要维护原树,只维护辅助树即可。
有一棵树:
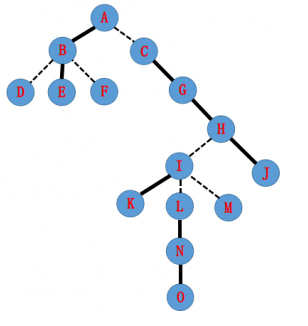
他构造出来的其中一种辅助树可能是这样(每个绿框内的子树表示一棵Splay,也为原树中的一条实链):

维护辅助树需要的函数(列题注释):
【HNOI2010】弹飞绵羊(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<stack> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 200010; 9 10 int n, m; 11 int fa[N], lc[N], rc[N]; // 父节点 左儿子 右儿子 12 int rev[N], size1[N]; // 是否需要翻转 子树大小 13 int que[N], len; // 辅助用 14 int v[N]; 15 16 17 bool is_root(int x) // 判断是否为根 18 { 19 return !fa[x] || (lc[fa[x]] != x && rc[fa[x]] != x); 20 } 21 22 void pushup(int a) // 上传 23 { 24 size1[a] = 1; 25 if (lc[a]) size1[a] += size1[lc[a]]; 26 if (rc[a]) size1[a] += size1[rc[a]]; 27 } 28 29 void pushdown(int x) // 下传 翻转左右儿子 30 { 31 if (rev[x]) 32 { 33 swap(lc[x], rc[x]); 34 if (lc[x]) rev[lc[x]] ^= 1; 35 if (rc[x]) rev[rc[x]] ^= 1; 36 rev[x] = 0; 37 } 38 } 39 40 //Splay内容 41 42 int get(int x) // 判断是父节点的哪个儿子 43 { 44 return rc[fa[x]] == x; 45 } 46 47 void rotate(int x) // 旋转操作 48 { 49 int y = fa[x], z = fa[y], b = lc[y] == x ? rc[x] : lc[x]; 50 51 if (z && !is_root(y)) (lc[z] == y ? lc[z] : rc[z]) = x; 52 fa[x] = z; 53 fa[y] = x; 54 b ? fa[b] = y : 0; 55 56 if (x == lc[y]) 57 { 58 rc[x] = y; 59 lc[y] = b; 60 } 61 else 62 { 63 lc[x] = y; 64 rc[y] = b; 65 } 66 pushup(y); 67 pushup(x); 68 } 69 70 void splay(int x) // 将当前x节点旋转到Splay的根 71 { 72 int i, y; 73 que[len = 1] = x; 74 for (y = x; !is_root(y); y = fa[y]) que[++len] = fa[y]; 75 76 for (i = len; i >= 1; i--) pushdown(que[i]); 77 78 while (!is_root(x)) 79 { 80 if (!is_root(fa[x])) 81 { 82 if (get(x) == get(fa[x])) rotate(fa[x]); 83 else rotate(x); 84 } 85 rotate(x); 86 } 87 pushup(x); 88 } 89 90 // LCT 内容 91 92 void Access(int a) // 把从根到x的路径上的子节点放在一条重链(一棵Spay)里 93 { 94 int b; 95 for (b = 0; a; b = a, a = fa[a]) 96 { 97 splay(a); 98 rc[a] = b; 99 if (b) fa[b] = a; 100 pushup(a); 101 } 102 } 103 104 int Find_root(int a) // 找x所在树的根 105 { 106 Access(a); 107 splay(a); 108 while (pushdown(a), lc[a]) a = lc[a]; 109 splay(a); 110 return a; 111 } 112 113 void Make_root(int a) // 使a旋转到树的根 114 { 115 Access(a); 116 splay(a); 117 rev[a] ^= 1; 118 } 119 120 void Link(int a, int b) // 连边 121 { 122 Make_root(a); 123 fa[a] = b; 124 } 125 126 void Cut(int a, int b) // 删边 127 { 128 Make_root(a); 129 Access(b); 130 splay(b); 131 132 lc[b] = 0; 133 fa[a] = 0; 134 pushup(b); 135 } 136 137 int Select(int a, int b) // 求从a到b的距离 138 { 139 Make_root(a); 140 Access(b); 141 splay(b); 142 return size1[b] - 1; 143 } 144 145 int main() 146 { 147 scanf("%d", &n); 148 for (int i = 1; i <= n; i++) size1[i] = 1; 149 for (int i = 1; i <= n; i++) 150 { 151 scanf("%d", &v[i]); 152 if (i + v[i] > n) Link(i, n + 1); 153 else Link(i, i + v[i]); 154 } 155 156 int q; 157 scanf("%d", &q); 158 while (q--) 159 { 160 int op; 161 scanf("%d", &op); 162 if (op == 1) 163 { 164 int x; 165 scanf("%d", &x); 166 x++; 167 printf("%d\n", Select(x, n + 1)); 168 } 169 else 170 { 171 int x, k; 172 scanf("%d%d", &x, &k); 173 x++; 174 Cut(x, x + v[x] > n ? n + 1 : x + v[x]); 175 Link(x, x + k > n ? n + 1 : x + k); 176 v[x] = k; 177 } 178 } 179 }
维护树链信息:
LCT通过split(x,y)操作,可以将从x到y的路径提取到以y为根的Splay内,这样就可以方便的维护树链信息,比树链剖分少一个O(log n)的时间复杂度。
【国家集训队】TreeⅡ(题目):
模板
辅助树每个节点的权值为左右儿子的和,进行加乘时做标记下传,求和时将要求的路径放在同一棵Slpay里,再将其中一个节点转移到树的根,当前节点的权值即为路径的和

1 #include<cstdio> 2 #include<cstring> 3 #include<stack> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 typedef unsigned long long ULL; 9 10 const int N = 100010, mod = 51061; 11 12 ULL n; 13 ULL stk[N]; 14 ULL son[N][2], fa[N], size1[N]; 15 ULL v[N], s[N], la[N], lm[N]; 16 bool rev[N]; 17 18 bool no_root(ULL a) 19 { 20 return son[fa[a]][0] == a || son[fa[a]][1] == a; 21 } 22 23 void push_add(ULL a, ULL c) 24 { 25 s[a] = (s[a] + c * size1[a]) % mod; 26 v[a] = (v[a] + c) % mod; 27 la[a] = (la[a] + c) % mod; 28 } 29 30 void push_mul(ULL a, ULL c) 31 { 32 s[a] = (s[a] * c) % mod; 33 v[a] = (v[a] * c) % mod; 34 lm[a] = (lm[a] * c) % mod; 35 la[a] = (la[a] * c) % mod; 36 } 37 38 void push_rev(ULL a) 39 { 40 swap(son[a][0], son[a][1]); 41 rev[a] ^= 1; 42 } 43 44 void pushup(ULL a) 45 { 46 s[a] = (s[son[a][0]] + s[son[a][1]] + v[a]) % mod; 47 size1[a] = size1[son[a][0]] + size1[son[a][1]] + 1; 48 } 49 50 void pushdown(ULL a) 51 { 52 if (lm[a] != 1) 53 { 54 push_mul(son[a][0], lm[a]); 55 push_mul(son[a][1], lm[a]); 56 lm[a] = 1; 57 } 58 if (la[a]) 59 { 60 push_add(son[a][0], la[a]); 61 push_add(son[a][1], la[a]); 62 la[a] = 0; 63 } 64 if (rev[a]) 65 { 66 if (son[a][0]) push_rev(son[a][0]); 67 if (son[a][1]) push_rev(son[a][1]); 68 rev[a] = 0; 69 } 70 } 71 72 void rotate(ULL a) 73 { 74 ULL b = fa[a], c = fa[b]; 75 ULL k = son[b][1] == a, w = son[a][!k]; 76 77 if (no_root(b)) son[c][son[c][1] == b] = a; 78 son[a][!k] = b; 79 son[b][k] = w; 80 81 if (w) fa[w] = b; 82 fa[b] = a; 83 fa[a] = c; 84 pushup(b); 85 } 86 87 void splay(ULL x) 88 { 89 ULL y = x, z = 0; 90 stk[++z] = y; 91 92 while (no_root(y)) stk[++z] = y = fa[y]; 93 while (z) pushdown(stk[z--]); 94 95 while (no_root(x)) 96 { 97 y = fa[x]; z = fa[y]; 98 if (no_root(y)) rotate((son[y][0] == x) ^ (son[z][0] == y) ? x : y); 99 rotate(x); 100 } 101 pushup(x); 102 } 103 104 void Access(ULL a) 105 { 106 for (ULL b = 0; a; a = fa[b = a]) 107 { 108 splay(a); 109 son[a][1] = b; 110 pushup(a); 111 } 112 } 113 114 void Make_root(ULL a) 115 { 116 Access(a); 117 splay(a); 118 push_rev(a); 119 } 120 121 void split(ULL a, ULL b) 122 { 123 Make_root(a); 124 Access(b); 125 splay(b); 126 } 127 128 void Cut(ULL a, ULL b) 129 { 130 split(a, b); 131 fa[a] = son[b][0] = 0; 132 } 133 134 void Link(ULL a, ULL b) 135 { 136 Make_root(a); 137 fa[a] = b; 138 } 139 140 int main() 141 { 142 ULL q; 143 scanf("%llu%llu", &n, &q); 144 145 for (ULL i = 1; i <= n; i++) 146 { 147 size1[i] = 1; 148 lm[i] = 1; 149 v[i] = 1; 150 } 151 152 for (ULL i = 1; i < n; i++) 153 { 154 ULL a, b; 155 scanf("%llu%llu", &a, &b); 156 Link(a, b); 157 } 158 159 while (q--) 160 { 161 char op[5]; 162 scanf("%s", op); 163 164 if (op[0] == '+') 165 { 166 ULL a, b; 167 ULL c; 168 scanf("%llu%llu%llu", &a, &b, &c); 169 split(a, b); 170 push_add(b, c); 171 } 172 else if (op[0] == '-') 173 { 174 ULL a, b; 175 scanf("%llu%llu", &a, &b); 176 Cut(a, b); 177 scanf("%llu%llu", &a, &b); 178 Link(a, b); 179 } 180 else if (op[0] == '*') 181 { 182 ULL a, b; 183 ULL c; 184 scanf("%llu%llu%llu", &a, &b, &c); 185 split(a, b); 186 push_mul(b, c); 187 } 188 else if (op[0] == '/') 189 { 190 ULL a, b; 191 scanf("%llu%llu", &a, &b); 192 split(a, b); 193 printf("%llu\n", s[b]); 194 } 195 } 196 }
【洛谷P3690】Link Cut Tree (题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<stack> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 typedef unsigned long long ULL; 9 10 const int N = 100010, mod = 51061; 11 12 ULL n; 13 ULL stk[N]; 14 ULL son[N][2], fa[N], size1[N]; 15 ULL v[N], s[N], la[N], lm[N]; 16 bool rev[N]; 17 18 bool no_root(ULL a) 19 { 20 return son[fa[a]][0] == a || son[fa[a]][1] == a; 21 } 22 23 void push_rev(ULL a) 24 { 25 swap(son[a][0], son[a][1]); 26 rev[a] ^= 1; 27 } 28 29 void pushup(ULL a) 30 { 31 s[a] = s[son[a][0]] ^ s[son[a][1]] ^ v[a]; 32 size1[a] = size1[son[a][0]] + size1[son[a][1]] + 1; 33 } 34 35 void pushdown(ULL a) 36 { 37 if (rev[a]) 38 { 39 if (son[a][0]) push_rev(son[a][0]); 40 if (son[a][1]) push_rev(son[a][1]); 41 rev[a] = 0; 42 } 43 } 44 45 void rotate(ULL a) 46 { 47 ULL b = fa[a], c = fa[b]; 48 ULL k = son[b][1] == a, w = son[a][!k]; 49 50 if (no_root(b)) son[c][son[c][1] == b] = a; 51 son[a][!k] = b; 52 son[b][k] = w; 53 54 if (w) fa[w] = b; 55 fa[b] = a; 56 fa[a] = c; 57 pushup(b); 58 } 59 60 void splay(ULL x) 61 { 62 ULL y = x, z = 0; 63 stk[++z] = y; 64 65 while (no_root(y)) stk[++z] = y = fa[y]; 66 while (z) pushdown(stk[z--]); 67 68 while (no_root(x)) 69 { 70 y = fa[x]; z = fa[y]; 71 if (no_root(y)) rotate((son[y][0] == x) ^ (son[z][0] == y) ? x : y); 72 rotate(x); 73 } 74 pushup(x); 75 } 76 77 void Access(ULL a) 78 { 79 for (ULL b = 0; a; a = fa[b = a]) 80 { 81 splay(a); 82 son[a][1] = b; 83 pushup(a); 84 } 85 } 86 87 void Make_root(ULL a) 88 { 89 Access(a); 90 splay(a); 91 push_rev(a); 92 } 93 94 void split(ULL a, ULL b) 95 { 96 Make_root(a); 97 Access(b); 98 splay(b); 99 } 100 101 int find_root(ULL x) 102 { 103 Access(x); 104 splay(x); 105 while (son[x][0]) pushdown(x), x = son[x][0]; 106 splay(x); 107 return x; 108 } 109 110 void Cut(ULL a, ULL b) 111 { 112 Make_root(a); 113 if (find_root(b) == a && fa[b] == a && son[b][0] == 0) 114 { 115 fa[b] = son[a][1] = 0; 116 pushup(a); 117 } 118 } 119 120 void Link(ULL a, ULL b) 121 { 122 Make_root(a); 123 if (find_root(b) != a) fa[a] = b; 124 } 125 126 int main() 127 { 128 ULL m; 129 scanf("%llu%llu", &n, &m); 130 for (int i = 1; i <= n; i++) scanf("%d", &v[i]); 131 132 while (m--) 133 { 134 ULL op; 135 ULL x, y; 136 scanf("%llu%llu%llu", &op, &x, &y); 137 switch (op) 138 { 139 case 0: 140 { 141 split(x, y); 142 printf("%llu\n", s[y]); 143 break; 144 } 145 case 1: 146 { 147 Link(x, y); 148 break; 149 } 150 case 2: 151 { 152 Cut(x, y); 153 break; 154 } 155 case 3: 156 { 157 splay(x); 158 v[x] = y; 159 break; 160 } 161 } 162 } 163 164 }
【SDOI2011】染色(题目):
其实单纯的树链剖分更简单
每个节点存储代表区间最左边的颜色,代表区间最右边的颜色,当前节点的颜色,颜色种数。pushup时左儿子颜色种数+右儿子颜色种数+1(当前节点),若左儿子最右边的颜色与当前节点颜色相同则要减一,右儿子同样(因为左右儿子代表的区间是不包括当前节点的,和线段树不一样)。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 100010; 8 9 int n; 10 int col[N], rcol[N], lcol[N]; 11 int fa[N], son[N][2]; 12 int tag[N], s[N]; 13 int stk[N]; 14 bool rev[N]; 15 16 bool no_root(int x) 17 { 18 return son[fa[x]][0] == x || son[fa[x]][1] == x; 19 } 20 21 void push_rev(int x) 22 { 23 if (!x) return; 24 25 rev[x] ^= 1; 26 swap(son[x][0], son[x][1]); 27 swap(lcol[x], rcol[x]); 28 } 29 30 void push_col(int x, int c) 31 { 32 if (!x) return; 33 34 tag[x] = c; 35 col[x] = rcol[x] = lcol[x] = c; 36 s[x] = 1; 37 } 38 39 void pushup(int x) 40 { 41 lcol[x] = son[x][0] ? lcol[son[x][0]] : col[x]; 42 rcol[x] = son[x][1] ? rcol[son[x][1]] : col[x]; 43 44 if (son[x][0] && son[x][1]) s[x] = s[son[x][0]] + s[son[x][1]] + 1 - (rcol[son[x][0]] == col[x]) - (lcol[son[x][1]] == col[x]); 45 else if (son[x][0]) s[x] = s[son[x][0]] + 1 - (rcol[son[x][0]] == col[x]); 46 else if (son[x][1]) s[x] = s[son[x][1]] + 1 - (lcol[son[x][1]] == col[x]); 47 else s[x] = 1; 48 } 49 50 void pushdown(int x) 51 { 52 if (rev[x]) 53 { 54 push_rev(son[x][1]); 55 push_rev(son[x][0]); 56 rev[x] = 0; 57 } 58 if (tag[x]) 59 { 60 push_col(son[x][0], tag[x]); 61 push_col(son[x][1], tag[x]); 62 tag[x] = 0; 63 } 64 } 65 66 void rotate(int x) 67 { 68 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 69 70 if (no_root(y)) son[z][son[z][1] == y] = x; 71 son[y][k] = w; 72 son[x][!k] = y; 73 if (w) fa[w] = y; 74 fa[x] = z; 75 fa[y] = x; 76 pushup(y); 77 } 78 79 void splay(int x) 80 { 81 int y = x, z = 0; 82 83 stk[++z] = y; 84 while (no_root(y)) 85 { 86 y = fa[y]; 87 stk[++z] = y; 88 } 89 while (z) pushdown(stk[z--]); 90 91 while (no_root(x)) 92 { 93 y = fa[x], z = fa[y]; 94 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 95 rotate(x); 96 } 97 pushup(x); 98 } 99 100 void Access(int x) 101 { 102 for (int y = 0; x; x = fa[y = x]) 103 { 104 splay(x); 105 son[x][1] = y; 106 pushup(x); 107 } 108 } 109 110 void Make_root(int x) 111 { 112 Access(x); 113 splay(x); 114 push_rev(x); 115 } 116 117 void split(int x, int y) 118 { 119 Make_root(x); 120 Access(y); 121 splay(y); 122 } 123 124 void Link(int x, int y) 125 { 126 Make_root(x); 127 fa[x] = y; 128 } 129 130 int main() 131 { 132 int m; 133 scanf("%d%d", &n, &m); 134 for (int i = 1; i <= n; i++) 135 { 136 scanf("%d", &col[i]); 137 rcol[i] = lcol[i] = col[i]; 138 s[i] = 1; 139 } 140 for (int i = 1; i < n; i++) 141 { 142 int x, y; 143 scanf("%d%d", &x, &y); 144 Link(x, y); 145 } 146 147 while (m--) 148 { 149 char op[5]; 150 int x, y; 151 scanf("%s%d%d", op, &x, &y); 152 153 split(x, y); 154 155 if (op[0] == 'Q') printf("%d\n", s[y]); 156 else 157 { 158 int z; 159 scanf("%d", &z); 160 push_col(y, z); 161 } 162 } 163 }
【SHOI2014】三叉神经树(题目):
预处理出每个节点的子节点的1的数量和d(i,0/1),d(i,0/1)表示若在当前节点额外输入一个0/1,它所在的链的链顶输出为什么(pushup更新特殊,代码解释)。
虽然每个节点有三个儿子,但需要修改某个节点时再将它的父亲的左/右儿子变成它,对答案没有影响。
ps:时刻注意辅助树中每个节点的左儿子在原树中是他的祖先节点,这样pushup更新就更好理解。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 2000010; 8 9 int n; 10 int a[N], s[N], b[N][2]; 11 int fa[N], son[N][2]; 12 int h[N], nex[N], dqx; 13 14 void dfs(int u) 15 { 16 for (int i = h[u]; i; i = nex[i]) 17 { 18 if (i <= n) dfs(i); 19 s[u] += a[i]; 20 } 21 22 a[u] = b[u][0] = (s[u] >= 2); 23 b[u][1] = (s[u] >= 1); 24 } 25 26 bool no_root(int x) 27 { 28 return son[fa[x]][0] == x || son[fa[x]][1] == x; 29 } 30 31 void pushup(int x) 32 { 33 b[x][0] = (s[x] >= 2); 34 b[x][1] = (s[x] >= 1); 35 36 if (son[x][1]) 37 { 38 if (b[son[x][1]][0]) b[x][0] = b[x][1]; 39 else if (!b[son[x][1]][1]) b[x][1] = b[x][0]; 40 } 41 if (son[x][0]) 42 { 43 if (b[x][0]) b[x][0] = b[x][1] = b[son[x][0]][1]; 44 else if (!b[x][1]) b[x][0] = b[x][1] = b[son[x][0]][0]; 45 else b[x][0] = b[son[x][0]][0], b[x][1] = b[son[x][0]][1]; 46 } 47 } 48 49 void rotate(int x) 50 { 51 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 52 53 if (no_root(y)) son[z][son[z][1] == y] = x; 54 son[y][k] = w; 55 son[x][!k] = y; 56 if (w) fa[w] = y; 57 fa[x] = z; 58 fa[y] = x; 59 60 b[x][0] = b[y][0]; 61 b[x][1] = b[y][1]; 62 63 pushup(y); 64 } 65 66 void splay(int x) 67 { 68 while (no_root(x)) 69 { 70 int y = fa[x], z = fa[y]; 71 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 72 rotate(x); 73 } 74 pushup(x); 75 } 76 77 void Access(int x) 78 { 79 for (int y = 0; x; x = fa[y = x]) 80 { 81 splay(x); 82 s[x] += b[son[x][1]][0]; 83 son[x][1] = y; 84 s[x] -= b[y][0]; 85 86 pushup(x); 87 } 88 } 89 90 int main() 91 { 92 scanf("%d", &n); 93 94 for (int i = 1; i <= n; i++) 95 { 96 int x; 97 scanf("%d", &x); 98 fa[x] = i; 99 nex[x] = h[i]; 100 h[i] = x; 101 102 scanf("%d", &x); 103 fa[x] = i; 104 nex[x] = h[i]; 105 h[i] = x; 106 107 scanf("%d", &x); 108 fa[x] = i; 109 nex[x] = h[i]; 110 h[i] = x; 111 } 112 for (int i = n + 1; i <= 3 * n + 1; i++) scanf("%d", &a[i]); 113 114 dfs(1); 115 116 int q; 117 scanf("%d", &q); 118 while (q--) 119 { 120 int x; 121 scanf("%d", &x); 122 123 Access(fa[x]); 124 splay(fa[x]); 125 126 a[x] ^= 1; 127 a[x] ? s[fa[x]]++ : s[fa[x]]--; 128 129 pushup(x); 130 Access(1); 131 splay(1); 132 133 printf("%d\n", b[1][0]); 134 } 135 }
维护联通性质:
使用Find(x)函数,可以方便的判断两个点是否在同一棵树上。
【SDOI2008】洞穴探测(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 100010; 8 9 int n; 10 int son[N][2], fa[N], rev[N]; 11 12 bool no_root(int x) 13 { 14 return son[fa[x]][0] == x || son[fa[x]][1] == x; 15 } 16 17 void pushdown(int x) 18 { 19 if (!rev[x]) return; 20 21 int lc = son[x][0], rc = son[x][1]; 22 if (lc) swap(son[lc][0], son[lc][1]), rev[lc] ^= 1; 23 if (rc) swap(son[rc][0], son[rc][1]), rev[rc] ^= 1; 24 rev[x] = 0; 25 } 26 27 void update(int x) 28 { 29 if (no_root(x)) update(fa[x]); 30 pushdown(x); 31 } 32 33 void rotate(int x) 34 { 35 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 36 37 if (no_root(y)) son[z][son[z][1] == y] = x; 38 son[y][k] = w; 39 son[x][!k] = y; 40 if (w) fa[w] = y; 41 fa[y] = x; 42 fa[x] = z; 43 } 44 45 void splay(int x) 46 { 47 update(x); 48 49 while (no_root(x)) 50 { 51 int y = fa[x], z = fa[y]; 52 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 53 rotate(x); 54 } 55 } 56 57 void Access(int x) 58 { 59 for (int y = 0; x; x = fa[y = x]) 60 { 61 splay(x); 62 son[x][1] = y; 63 } 64 } 65 66 void Make_root(int x) 67 { 68 Access(x); 69 splay(x); 70 swap(son[x][0], son[x][1]); 71 rev[x] ^= 1; 72 } 73 74 int Find(int x) 75 { 76 Access(x); 77 splay(x); 78 while (son[x][0]) x = son[x][0]; 79 splay(x); 80 return x; 81 } 82 83 void Link(int x, int y) 84 { 85 if (Find(x) == Find(y)) return; 86 Make_root(x); 87 fa[x] = y; 88 } 89 90 void Cut(int x, int y) 91 { 92 Make_root(x); 93 Access(y); 94 splay(y); 95 if (son[y][0] == x && !son[x][1]) fa[x] = son[y][0] = 0; 96 } 97 98 int main() 99 { 100 int m; 101 scanf("%d%d", &n, &m); 102 103 while (m--) 104 { 105 char op[10]; 106 int x, y; 107 scanf("%s%d%d", op, &x, &y); 108 if (op[0] == 'C') 109 { 110 Link(x, y); 111 } 112 else if (op[0] == 'D') 113 { 114 Cut(x, y); 115 } 116 else if (op[0] == 'Q') 117 { 118 puts(Find(x) == Find(y) ? "Yes" : "No"); 119 } 120 } 121 }
【洛谷P3950】部落冲突(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 typedef pair<int, int> PII; 9 10 const int N = 2000010; 11 12 int n; 13 int son[N][2], fa[N], rev[N]; 14 15 bool no_root(int x) 16 { 17 return son[fa[x]][0] == x || son[fa[x]][1] == x; 18 } 19 20 void pushdown(int x) 21 { 22 if (!rev[x]) return; 23 24 int lc = son[x][0], rc = son[x][1]; 25 if (lc) swap(son[lc][0], son[lc][1]), rev[lc] ^= 1; 26 if (rc) swap(son[rc][0], son[rc][1]), rev[rc] ^= 1; 27 rev[x] = 0; 28 } 29 30 void update(int x) 31 { 32 if (no_root(x)) update(fa[x]); 33 pushdown(x); 34 } 35 36 void rotate(int x) 37 { 38 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 39 40 if (no_root(y)) son[z][son[z][1] == y] = x; 41 son[y][k] = w; 42 son[x][!k] = y; 43 if (w) fa[w] = y; 44 fa[y] = x; 45 fa[x] = z; 46 } 47 48 void splay(int x) 49 { 50 update(x); 51 52 while (no_root(x)) 53 { 54 int y = fa[x], z = fa[y]; 55 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 56 rotate(x); 57 } 58 } 59 60 void Access(int x) 61 { 62 for (int y = 0; x; x = fa[y = x]) 63 { 64 splay(x); 65 son[x][1] = y; 66 } 67 } 68 69 void Make_root(int x) 70 { 71 Access(x); 72 splay(x); 73 swap(son[x][0], son[x][1]); 74 rev[x] ^= 1; 75 } 76 77 int Find(int x) 78 { 79 Access(x); 80 splay(x); 81 while (son[x][0]) x = son[x][0]; 82 splay(x); 83 return x; 84 } 85 86 void Link(int x, int y) 87 { 88 if (Find(x) == Find(y)) return; 89 Make_root(x); 90 fa[x] = y; 91 } 92 93 void Cut(int x, int y) 94 { 95 Make_root(x); 96 Access(y); 97 splay(y); 98 if (son[y][0] == x && !son[x][1]) fa[x] = son[y][0] = 0; 99 } 100 101 int main() 102 { 103 int m; 104 scanf("%d%d", &n, &m); 105 106 for (int i = 1; i < n; i++) 107 { 108 int x, y; 109 scanf("%d%d", &x, &y); 110 Link(x, y); 111 } 112 113 vector<PII> war; 114 while (m--) 115 { 116 char op[10]; 117 int x, y; 118 scanf("%s", op); 119 if (op[0] == 'U') 120 { 121 int k; 122 scanf("%d", &k); 123 k--; 124 125 x = war[k].first, y = war[k].second; 126 Link(x, y); 127 } 128 else if (op[0] == 'C') 129 { 130 scanf("%d%d", &x, &y); 131 132 Cut(x, y); 133 war.push_back(make_pair(x, y)); 134 } 135 else if (op[0] == 'Q') 136 { 137 scanf("%d%d", &x, &y); 138 puts(Find(x) == Find(y) ? "Yes" : "No"); 139 } 140 } 141 }
维护双联通分量:
新加一条边时,若两点之前并不联通,则把这条边加上,否则在LCT上遍历两个点之间的路径,将路径上的点更新并查集进行缩点操作。
【AHOI2005】航线规划(题目):
离线逆操作,将不需要删除的边全部加上,再逆向操作,每次删边相当于逆向加边。

1 #include<cstdio> 2 #include<cstring> 3 #include<map> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 200010; 9 10 11 int n, m, q, x, y, cur; 12 int f[N], ans[N]; 13 14 struct oper 15 { 16 int op, a, b; 17 } s[N]; 18 19 map<pair<int, int>, int> mp; 20 21 int findp(int x) 22 { 23 return f[x] ? f[x] = findp(f[x]) : x; 24 } 25 26 void merge(int x, int y) 27 { 28 x = findp(x); 29 y = findp(y); 30 if (x != y) f[x] = y; 31 } 32 33 struct Splay 34 { 35 int ch[N][2], fa[N], tag[N], siz[N]; 36 37 void clear(int x) 38 { 39 ch[x][0] = ch[x][1] = fa[x] = tag[x] = siz[x] = 0; 40 } 41 42 int getch(int x) 43 { 44 return ch[findp(fa[x])][1] == x; 45 } 46 47 int isroot(int x) 48 { 49 return ch[findp(fa[x])][0] != x && ch[findp(fa[x])][1] != x; 50 } 51 52 void maintain(int x) 53 { 54 clear(0); 55 if (x) siz[x] = siz[ch[x][0]] + 1 + siz[ch[x][1]]; 56 } 57 58 void pushdown(int x) 59 { 60 if (tag[x]) { 61 if (ch[x][0]) tag[ch[x][0]] ^= 1, swap(ch[ch[x][0]][0], ch[ch[x][0]][1]); 62 if (ch[x][1]) tag[ch[x][1]] ^= 1, swap(ch[ch[x][1]][0], ch[ch[x][1]][1]); 63 tag[x] = 0; 64 } 65 } 66 67 void print(int x) 68 { 69 if (!x) return; 70 pushdown(x); 71 print(ch[x][0]); 72 printf("%d ", x); 73 print(ch[x][1]); 74 } 75 76 void update(int x) 77 { 78 if (!isroot(x)) update(findp(fa[x])); 79 pushdown(x); 80 } 81 82 void rotate(int x) 83 { 84 x = findp(x); 85 86 int y = findp(fa[x]), z = findp(fa[y]), chx = getch(x), chy = getch(y); 87 fa[x] = z; 88 89 if (!isroot(y)) ch[z][chy] = x; 90 ch[y][chx] = ch[x][chx ^ 1]; 91 fa[ch[x][chx ^ 1]] = y; 92 ch[x][chx ^ 1] = y; 93 fa[y] = x; 94 95 maintain(y); 96 maintain(x); 97 if (z) maintain(z); 98 } 99 100 void splay(int x) 101 { 102 x = findp(x); 103 update(x); 104 for (int f = findp(fa[x]); f = findp(fa[x]), !isroot(x); rotate(x)) 105 if (!isroot(f)) rotate(getch(x) == getch(f) ? f : x); 106 } 107 108 void Access(int x) 109 { 110 for (int f = 0; x; f = x, x = findp(fa[x])) 111 splay(x), ch[x][1] = f, maintain(x); 112 } 113 114 void Make_root(int x) 115 { 116 x = findp(x); 117 Access(x); 118 splay(x); 119 tag[x] ^= 1; 120 swap(ch[x][0], ch[x][1]); 121 } 122 123 int find(int x) 124 { 125 x = findp(x); 126 Access(x); 127 splay(x); 128 while (ch[x][0]) x = ch[x][0]; 129 splay(x); 130 return x; 131 } 132 133 void dfs(int x) 134 { 135 pushdown(x); 136 if (ch[x][0]) dfs(ch[x][0]), merge(ch[x][0], x); 137 if (ch[x][1]) dfs(ch[x][1]), merge(ch[x][1], x); 138 } 139 } st; 140 141 int main() 142 { 143 scanf("%d%d", &n, &m); 144 145 for (int i = 1; i <= n; i++) st.maintain(i); 146 for (int i = 1; i <= m; i++) 147 { 148 scanf("%d%d", &x, &y); 149 mp[{x, y}] = mp[{y, x}] = 1; 150 } 151 152 while (scanf("%d", &s[++q].op)) 153 { 154 if (s[q].op == -1) 155 { 156 q--; 157 break; 158 } 159 scanf("%d%d", &s[q].a, &s[q].b); 160 if (!s[q].op) mp[{s[q].a, s[q].b}] = mp[{s[q].b, s[q].a}] = 0; 161 } 162 163 reverse(s + 1, s + q + 1); 164 for (map<pair<int, int>, int>::iterator it = mp.begin(); it != mp.end(); it++) 165 { 166 if (it->second) 167 { 168 mp[{it->first.second, it->first.first}] = 0; 169 170 x = findp(it->first.first); 171 y = findp(it->first.second); 172 173 if (st.find(x) != st.find(y)) st.Make_root(x), st.fa[x] = y; 174 else 175 { 176 if (x == y) continue; 177 178 st.Make_root(x); 179 st.Access(y); 180 st.splay(y); 181 st.dfs(y); 182 183 int t = findp(y); 184 st.fa[t] = findp(st.fa[y]); 185 st.ch[t][0] = st.ch[t][1] = 0; 186 st.maintain(t); 187 } 188 } 189 } 190 191 for (int i = 1; i <= q; i++) 192 { 193 if (s[i].op == 0) 194 { 195 x = findp(s[i].a); 196 y = findp(s[i].b); 197 198 st.Make_root(x); 199 st.Access(y); 200 st.splay(y); 201 st.dfs(y); 202 203 int t = findp(y); 204 st.fa[t] = st.fa[y]; 205 st.ch[t][0] = st.ch[t][1] = 0; 206 st.maintain(t); 207 } 208 if (s[i].op == 1) 209 { 210 x = findp(s[i].a); 211 y = findp(s[i].b); 212 213 st.Make_root(x); 214 st.Access(y); 215 st.splay(y); 216 ans[++cur] = st.siz[y] - 1; 217 } 218 } 219 for (int i = cur; i >= 1; i--) printf("%d\n", ans[i]); 220 return 0; 221 }
维护边权:
若两个点之间有边,则新建一个节点,节点的权值为边权,该节点再分别连接边的两个端点。不代表边的节点权值为无穷大。
【洛谷P4234】最小差值生成树(题目):
将边从小到大遍历,遍历到某条边时,若该边的两个端点未联通,则正常加边,否则把两个端点之间的路径中边权最小的边删除,若所有点都联通则更新答案。
此题中的pushup操作为更新以当前节点为根的子树中权值最小的点(原图中的边)。

1 #include<cstdio> 2 #include<cstring> 3 #include<set> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 2000010; 9 10 int n, m; 11 int fa[N], son[N][2]; 12 int minn[N], val[N]; 13 int rev[N]; 14 15 16 struct Node 17 { 18 int a, b, v; 19 }; 20 21 Node s[N]; 22 23 multiset<int> st; 24 25 bool no_root(int x) 26 { 27 return son[fa[x]][0] == x || son[fa[x]][1] == x; 28 } 29 30 void pushup(int x) 31 { 32 if (!x) return; 33 minn[x] = x; 34 35 if (son[x][0]) 36 { 37 if (val[minn[son[x][0]]] < val[minn[x]]) minn[x] = minn[son[x][0]]; 38 } 39 if (son[x][1]) 40 { 41 if (val[minn[son[x][1]]] < val[minn[x]]) minn[x] = minn[son[x][1]]; 42 } 43 } 44 45 void pushdown(int x) 46 { 47 if (!rev[x]) return; 48 49 int lc = son[x][0], rc = son[x][1]; 50 if (lc) swap(son[lc][0], son[lc][1]), rev[lc] ^= 1; 51 if (rc) swap(son[rc][0], son[rc][1]), rev[rc] ^= 1; 52 rev[x] = 0; 53 } 54 55 void update(int x) 56 { 57 if (no_root(x)) update(fa[x]); 58 pushdown(x); 59 } 60 61 void rotate(int x) 62 { 63 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 64 65 if (no_root(y)) son[z][son[z][1] == y] = x; 66 son[y][k] = w; 67 son[x][!k] = y; 68 if (w) fa[w] = y; 69 fa[y] = x; 70 fa[x] = z; 71 72 pushup(y); 73 pushup(x); 74 if (z) pushup(z); 75 } 76 77 void splay(int x) 78 { 79 update(x); 80 while (no_root(x)) 81 { 82 int y = fa[x], z = fa[y]; 83 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 84 rotate(x); 85 } 86 } 87 88 void Access(int x) 89 { 90 for (int y = 0; x; x = fa[y = x]) 91 { 92 splay(x); 93 son[x][1] = y; 94 pushup(x); 95 } 96 } 97 98 void Make_root(int x) 99 { 100 Access(x); 101 splay(x); 102 rev[x] ^= 1; 103 swap(son[x][0], son[x][1]); 104 } 105 106 void Link(int x, int y) 107 { 108 Make_root(x); 109 fa[x] = y; 110 } 111 112 void Cut(int x, int y) 113 { 114 Make_root(x); 115 Access(y); 116 splay(y); 117 son[y][0] = fa[x] = 0; 118 pushup(y); 119 } 120 121 int Find(int x) 122 { 123 Access(x); 124 splay(x); 125 while (son[x][0]) x = son[x][0]; 126 splay(x); 127 return x; 128 } 129 130 bool com(Node a, Node b) 131 { 132 return a.v < b.v; 133 } 134 135 int main() 136 { 137 scanf("%d%d", &n, &m); 138 for (int i = 1; i <= n; i++) 139 { 140 val[i] = 2e9 + 7; 141 pushup(i); 142 } 143 for (int i = 1; i <= m; i++) scanf("%d%d%d", &s[i].a, &s[i].b, &s[i].v); 144 sort(s + 1, s + m + 1, com); 145 for (int i = 1; i <= m; i++) 146 { 147 val[i + n] = s[i].v; 148 pushup(i + n); 149 } 150 151 int num = 0, ans = 0; 152 for (int i = 1; i <= m; i++) 153 { 154 int x, y; 155 x = s[i].a, y = s[i].b; 156 157 if (x == y) continue; 158 if (Find(x) != Find(y)) 159 { 160 num++; 161 Link(x, i + n); 162 Link(i + n, y); 163 st.insert(s[i].v); 164 if (num == n - 1) ans = s[i].v - (*(st.begin()++)); 165 } 166 else 167 { 168 Make_root(x); 169 Access(y); 170 splay(y); 171 172 int t = minn[y] - n; 173 Cut(s[t].a, t + n); 174 Cut(t + n, s[t].b); 175 st.erase(st.find(s[t].v)); 176 Link(x, i + n); 177 Link(i + n, y); 178 st.insert(s[i].v); 179 if (num == n - 1) ans = min(ans, s[i].v - (*(st.begin()++))); 180 } 181 } 182 183 printf("%d", ans); 184 }
【WC2006】水管局长(题目):
把所有操作存入之后逆向离线操作,不会被删掉的边先加上,当边足够形成一个最小生成树时便逆向遍历所有操作,操作中每次删边相当于加边,每次加边时判断加上后答案会不会更小,会的话就加上,不会就忽略。表示边的节点权值为边的权值,其他店权值为0。
此题中pushup操作为更新以当前节点为根的子树中权值最大的点(原图中的边)。

1 #include<cstdio> 2 #include<cstring> 3 #include<map> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 typedef pair<int, int> PII; 9 10 const int N = 2000010; 11 12 int n, m; 13 int fa[N], son[N][2]; 14 int mx[N], val[N]; 15 int rev[N]; 16 int ans[N]; 17 bool vis[N]; 18 19 struct Node 20 { 21 int a, b, v; 22 }; 23 24 Node s[N]; 25 26 struct Task 27 { 28 int x, y, op, id; 29 }; 30 31 Task tas[N]; 32 33 map<PII, int> id; 34 35 bool no_root(int x) 36 { 37 return son[fa[x]][0] == x || son[fa[x]][1] == x; 38 } 39 40 void pushup(int x) 41 { 42 if (!x) return; 43 mx[x] = val[x]; 44 45 if (s[mx[son[x][0]]].v > s[mx[x]].v) mx[x] = mx[son[x][0]]; 46 if (s[mx[son[x][1]]].v > s[mx[x]].v) mx[x] = mx[son[x][1]]; 47 } 48 49 void pushdown(int x) 50 { 51 if (!rev[x]) return; 52 53 int lc = son[x][0], rc = son[x][1]; 54 if (lc) swap(son[lc][0], son[lc][1]), rev[lc] ^= 1; 55 if (rc) swap(son[rc][0], son[rc][1]), rev[rc] ^= 1; 56 rev[x] = 0; 57 } 58 59 void update(int x) 60 { 61 if (no_root(x)) update(fa[x]); 62 pushdown(x); 63 } 64 65 void rotate(int x) 66 { 67 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 68 69 if (no_root(y)) son[z][son[z][1] == y] = x; 70 son[y][k] = w; 71 son[x][!k] = y; 72 if (w) fa[w] = y; 73 fa[y] = x; 74 fa[x] = z; 75 76 pushup(y); 77 pushup(x); 78 if (z) pushup(z); 79 } 80 81 void splay(int x) 82 { 83 update(x); 84 while (no_root(x)) 85 { 86 int y = fa[x], z = fa[y]; 87 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 88 rotate(x); 89 } 90 } 91 92 void Access(int x) 93 { 94 for (int y = 0; x; x = fa[y = x]) 95 { 96 splay(x); 97 son[x][1] = y; 98 pushup(x); 99 } 100 } 101 102 void Make_root(int x) 103 { 104 Access(x); 105 splay(x); 106 rev[x] ^= 1; 107 swap(son[x][0], son[x][1]); 108 } 109 110 void split(int x, int y) 111 { 112 Make_root(x); 113 Access(y); 114 splay(y); 115 } 116 117 void Link(int x, int y) 118 { 119 Make_root(x); 120 fa[x] = y; 121 } 122 123 void Cut(int x, int y) 124 { 125 Make_root(x); 126 Access(y); 127 splay(y); 128 son[y][0] = fa[x] = 0; 129 pushup(y); 130 } 131 132 int Find(int x) 133 { 134 Access(x); 135 splay(x); 136 while (son[x][0]) x = son[x][0]; 137 splay(x); 138 return x; 139 } 140 141 bool cmp(Node a, Node b) 142 { 143 return a.v < b.v; 144 } 145 146 void init(int x, int y) 147 { 148 fa[x] = son[x][0] = son[x][1] = val[x] = 0; 149 mx[x] = val[x] = y; 150 } 151 152 int main() 153 { 154 int q; 155 scanf("%d%d%d", &n, &m, &q); 156 157 for (int i = 1; i <= m; i++) 158 { 159 scanf("%d%d%d", &s[i].a, &s[i].b, &s[i].v); 160 if (s[i].a > s[i].b) swap(s[i].a, s[i].b); 161 } 162 163 sort(s + 1, s + 1 + m, cmp); 164 for (int i = 1; i <= m; i++) id[make_pair(s[i].a, s[i].b)] = i; 165 166 for (int i = 1; i <= q; i++) 167 { 168 scanf("%d%d%d", &tas[i].op, &tas[i].x, &tas[i].y); 169 if (tas[i].x > tas[i].y) swap(tas[i].x, tas[i].y); 170 if (tas[i].op == 2) 171 { 172 int d = id[make_pair(tas[i].x, tas[i].y)]; 173 tas[i].id = d; 174 vis[d] = 1; 175 } 176 } 177 178 for (int i = 1; i <= n + m; i++) init(i, i <= n ? 0 : (i - n)); 179 180 int sum = 0; 181 for (int i = 1; i <= m; i++) 182 { 183 if (!vis[i]) 184 { 185 if (sum == n - 1) break; 186 int x = s[i].a, y = s[i].b; 187 if (Find(x) == Find(y)) continue; 188 Link(x, i + n), Link(i + n, y); 189 sum++; 190 } 191 } 192 193 for (int i = q; i; i--) 194 { 195 int x = tas[i].x, y = tas[i].y; 196 if (tas[i].op == 1) 197 { 198 split(x, y); 199 ans[i] = s[mx[y]].v; 200 } 201 else 202 { 203 split(x, y); 204 int d = tas[i].id, t = mx[y]; 205 if (s[d].v < s[t].v) 206 { 207 Cut(x, t + n), Cut(y, t + n); 208 Link(x, d + n), Link(d + n, y); 209 } 210 } 211 } 212 213 for (int i = 1; i <= q; i++) 214 { 215 if (tas[i].op == 1) printf("%d\n", ans[i]); 216 } 217 }
【NOI2014】魔法森林(题目):
以Ai为关键字将每条边排序,再动态加边,每条路径的代价为其中B的最大值。

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 2e5 + 5; 9 10 int n, m; 11 int fa[N], lc[N], rc[N]; 12 int rev[N], que[N], len, val[N], sm[N], f[N]; 13 14 struct Node 15 { 16 int a, b, x, y; 17 } ask[N]; 18 19 int cx(int x) 20 { 21 if (f[x] != x) f[x] = cx(f[x]); 22 return f[x]; 23 } 24 25 void zm(int x, int y) 26 { 27 int ix = cx(x), iy = cx(y); 28 if (ix != iy) f[iy] = ix; 29 } 30 31 bool cmp(Node a, Node b) 32 { 33 return a.y < b.y; 34 } 35 36 int which(int x) 37 { 38 return rc[fa[x]] == x; 39 } 40 41 bool is_root(int x) 42 { 43 return !fa[x] || (lc[fa[x]] != x && rc[fa[x]] != x); 44 } 45 46 void upt(int x) 47 { 48 sm[x] = x; 49 if (lc[x] && val[sm[lc[x]]] > val[sm[x]]) sm[x] = sm[lc[x]]; 50 if (rc[x] && val[sm[rc[x]]] > val[sm[x]]) sm[x] = sm[rc[x]]; 51 } 52 53 void down(int x) 54 { 55 if (rev[x]) { 56 swap(lc[x], rc[x]); 57 if (lc[x]) rev[lc[x]] ^= 1; 58 if (rc[x]) rev[rc[x]] ^= 1; 59 rev[x] = 0; 60 } 61 } 62 63 void rotate(int x) 64 { 65 int y = fa[x], z = fa[y], b = lc[y] == x ? rc[x] : lc[x]; 66 if (z && !is_root(y)) (lc[z] == y ? lc[z] : rc[z]) = x; 67 fa[x] = z; fa[y] = x; b ? fa[b] = y : 0; 68 if (lc[y] == x) rc[x] = y, lc[y] = b; 69 else lc[x] = y, rc[y] = b; upt(y); upt(x); 70 } 71 72 void splay(int x) 73 { 74 int i, y; 75 que[len = 1] = x; 76 for (y = x; !is_root(y); y = fa[y]) que[++len] = fa[y]; 77 for (i = len; i >= 1; i--) down(que[i]); 78 79 while (!is_root(x)) 80 { 81 if (!is_root(fa[x])) 82 { 83 if (which(x) == which(fa[x])) rotate(fa[x]); 84 else rotate(x); 85 } 86 rotate(x); 87 } 88 upt(x); 89 } 90 91 void Access(int x) 92 { 93 int y; 94 for (y = 0; x; y = x, x = fa[x]) 95 { 96 splay(x); 97 rc[x] = y; 98 if (y) fa[y] = x; 99 upt(x); 100 } 101 } 102 103 int Find_Root(int x) 104 { 105 Access(x); 106 splay(x); 107 while (down(x), lc[x]) x = lc[x]; 108 splay(x); 109 return x; 110 } 111 112 void Make_Root(int x) 113 { 114 Access(x); 115 splay(x); 116 rev[x] ^= 1; 117 } 118 119 void Link(int x, int y) 120 { 121 Make_Root(x); 122 fa[x] = y; 123 } 124 125 void Cut(int x, int y) 126 { 127 Make_Root(x); 128 Access(y); 129 splay(y); 130 lc[y] = 0; 131 fa[x] = 0; 132 upt(y); 133 } 134 135 int Select(int x, int y) 136 { 137 Make_Root(x); 138 Access(y); 139 splay(y); 140 return sm[y]; 141 } 142 143 int main() 144 { 145 int ans = 2e9; 146 scanf("%d%d", &n, &m); 147 for (int i = 1; i <= m; i++) 148 { 149 int a, b, x, y; 150 scanf("%d%d%d%d", &a, &b, &x, &y); 151 ask[i].a = a, ask[i].b = b; 152 ask[i].x = x, ask[i].y = y; 153 } 154 155 sort(ask + 1, ask + m + 1, cmp); 156 for (int i = 1; i <= n + m; i++) f[i] = sm[i] = i; 157 for (int i = n + 1; i <= n + m; i++) val[i] = ask[i - n].x; 158 159 for (int i = 1; i <= m; i++) 160 { 161 int u = ask[i].a, v = ask[i].b; bool flag = 1; 162 if (cx(u) == cx(v)) 163 { 164 int w = Select(u, v); 165 if (val[w] > ask[i].x) Cut(ask[w - n].a, w), Cut(w, ask[w - n].b); 166 else flag = 0; 167 } 168 else zm(u, v); 169 170 if (flag) Link(u, i + n), Link(i + n, v); 171 if (cx(1) == cx(n)) ans = min(ans, ask[i].y + val[Select(1, n)]); 172 } 173 174 if (ans < 2e9) printf("%d\n", ans); 175 else printf("-1\n"); 176 return 0; 177 }
维护子树信息:
每个节点统计所有的虚儿子(父亲为x,但x在splay中的左右儿子不包括它)所代表的子树的贡献,pushup时对虚儿子和左右儿子同时更新。
【BJOI2014】大融和(题目):
模板

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 2e5 + 5; 9 10 int n, m; 11 int fa[N], lc[N], rc[N]; 12 int rev[N], que[N], len, val[N], sm[N], f[N]; 13 14 struct Node 15 { 16 int a, b, x, y; 17 } ask[N]; 18 19 int cx(int x) 20 { 21 if (f[x] != x) f[x] = cx(f[x]); 22 return f[x]; 23 } 24 25 void zm(int x, int y) 26 { 27 int ix = cx(x), iy = cx(y); 28 if (ix != iy) f[iy] = ix; 29 } 30 31 bool cmp(Node a, Node b) 32 { 33 return a.y < b.y; 34 } 35 36 int which(int x) 37 { 38 return rc[fa[x]] == x; 39 } 40 41 bool is_root(int x) 42 { 43 return !fa[x] || (lc[fa[x]] != x && rc[fa[x]] != x); 44 } 45 46 void upt(int x) 47 { 48 sm[x] = x; 49 if (lc[x] && val[sm[lc[x]]] > val[sm[x]]) sm[x] = sm[lc[x]]; 50 if (rc[x] && val[sm[rc[x]]] > val[sm[x]]) sm[x] = sm[rc[x]]; 51 } 52 53 void down(int x) 54 { 55 if (rev[x]) { 56 swap(lc[x], rc[x]); 57 if (lc[x]) rev[lc[x]] ^= 1; 58 if (rc[x]) rev[rc[x]] ^= 1; 59 rev[x] = 0; 60 } 61 } 62 63 void rotate(int x) 64 { 65 int y = fa[x], z = fa[y], b = lc[y] == x ? rc[x] : lc[x]; 66 if (z && !is_root(y)) (lc[z] == y ? lc[z] : rc[z]) = x; 67 fa[x] = z; fa[y] = x; b ? fa[b] = y : 0; 68 if (lc[y] == x) rc[x] = y, lc[y] = b; 69 else lc[x] = y, rc[y] = b; upt(y); upt(x); 70 } 71 72 void splay(int x) 73 { 74 int i, y; 75 que[len = 1] = x; 76 for (y = x; !is_root(y); y = fa[y]) que[++len] = fa[y]; 77 for (i = len; i >= 1; i--) down(que[i]); 78 79 while (!is_root(x)) 80 { 81 if (!is_root(fa[x])) 82 { 83 if (which(x) == which(fa[x])) rotate(fa[x]); 84 else rotate(x); 85 } 86 rotate(x); 87 } 88 upt(x); 89 } 90 91 void Access(int x) 92 { 93 int y; 94 for (y = 0; x; y = x, x = fa[x]) 95 { 96 splay(x); 97 rc[x] = y; 98 if (y) fa[y] = x; 99 upt(x); 100 } 101 } 102 103 int Find_Root(int x) 104 { 105 Access(x); 106 splay(x); 107 while (down(x), lc[x]) x = lc[x]; 108 splay(x); 109 return x; 110 } 111 112 void Make_Root(int x) 113 { 114 Access(x); 115 splay(x); 116 rev[x] ^= 1; 117 } 118 119 void Link(int x, int y) 120 { 121 Make_Root(x); 122 fa[x] = y; 123 } 124 125 void Cut(int x, int y) 126 { 127 Make_Root(x); 128 Access(y); 129 splay(y); 130 lc[y] = 0; 131 fa[x] = 0; 132 upt(y); 133 } 134 135 int Select(int x, int y) 136 { 137 Make_Root(x); 138 Access(y); 139 splay(y); 140 return sm[y]; 141 } 142 143 int main() 144 { 145 int ans = 2e9; 146 scanf("%d%d", &n, &m); 147 for (int i = 1; i <= m; i++) 148 { 149 int a, b, x, y; 150 scanf("%d%d%d%d", &a, &b, &x, &y); 151 ask[i].a = a, ask[i].b = b; 152 ask[i].x = x, ask[i].y = y; 153 } 154 155 sort(ask + 1, ask + m + 1, cmp); 156 for (int i = 1; i <= n + m; i++) f[i] = sm[i] = i; 157 for (int i = n + 1; i <= n + m; i++) val[i] = ask[i - n].x; 158 159 for (int i = 1; i <= m; i++) 160 { 161 int u = ask[i].a, v = ask[i].b; bool flag = 1; 162 if (cx(u) == cx(v)) 163 { 164 int w = Select(u, v); 165 if (val[w] > ask[i].x) Cut(ask[w - n].a, w), Cut(w, ask[w - n].b); 166 else flag = 0; 167 } 168 else zm(u, v); 169 170 if (flag) Link(u, i + n), Link(i + n, v); 171 if (cx(1) == cx(n)) ans = min(ans, ask[i].y + val[Select(1, n)]); 172 } 173 174 if (ans < 2e9) printf("%d\n", ans); 175 else printf("-1\n"); 176 return 0; 177 }
【洛谷P4299】首都(题目):
每次修改用二分查找树的重心的位置。

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 100009, INF = 2e9 + 7; 8 9 int f[N], son[N][2]; 10 int si[N], s[N], h[N]; 11 bool r[N]; 12 13 bool no_root(int x) 14 { 15 return son[f[x]][0] == x || son[f[x]][1] == x; 16 } 17 18 void pushup(int x) 19 { 20 s[x] = s[son[x][0]] + s[son[x][1]] + si[x] + 1; 21 } 22 23 void pushdown(int x) 24 { 25 if (r[x]) 26 { 27 int t = son[x][0]; 28 son[x][0] = son[x][1]; 29 son[x][1] = t; 30 r[son[x][0]] ^= 1; 31 r[son[x][1]] ^= 1; 32 r[x] = 0; 33 } 34 } 35 36 void update(int x) 37 { 38 if (no_root(x)) update(f[x]); 39 pushdown(x); 40 } 41 42 void rotate(int x) 43 { 44 int y = f[x], z = f[y], k = son[y][1] == x, w = son[x][!k]; 45 46 if (no_root(y)) son[z][son[z][1] == y] = x; 47 f[f[f[son[son[x][!k] = y][k] = w] = y] = x] = z; 48 49 pushup(y); 50 } 51 52 void splay(int x) 53 { 54 update(x); 55 int y; 56 while (no_root(x)) 57 { 58 if (no_root(y = f[x]))rotate((son[f[y]][0] == y) ^ (son[y][0] == x) ? x : y); 59 rotate(x); 60 } 61 pushup(x); 62 } 63 64 void Access(int x) 65 { 66 for (int y = 0; x; x = f[y = x]) 67 { 68 splay(x); 69 si[x] += s[son[x][1]]; 70 si[x] -= s[son[x][1] = y]; 71 pushup(x); 72 } 73 } 74 75 void Make_root(int x) 76 { 77 Access(x); 78 splay(x); 79 r[x] ^= 1; 80 } 81 82 void split(int x, int y) 83 { 84 Make_root(x); 85 Access(y); 86 splay(y); 87 } 88 89 void Link(int x, int y) 90 { 91 split(x, y); 92 si[f[x] = y] += s[x]; 93 pushup(y); 94 } 95 96 int geth(int x) 97 { 98 if (h[x] == x)return x; 99 return h[x] = geth(h[x]); 100 } 101 102 int push(int x) 103 { 104 int l, r; 105 int ji = s[x] & 1; 106 int sum = s[x] >> 1, lsum = 0, rsum = 0; 107 int newp = INF, nowl, nowr; 108 109 while (x) 110 { 111 pushdown(x); 112 nowl = s[l = son[x][0]] + lsum; nowr = s[r = son[x][1]] + rsum; 113 if (nowl <= sum && nowr <= sum) 114 { 115 if (ji) 116 { 117 newp = x; 118 break; 119 } 120 else if (newp > x) newp = x; 121 } 122 if (nowl < nowr) lsum += s[l] + si[x] + 1, x = r; 123 else rsum += s[r] + si[x] + 1, x = l; 124 } 125 splay(newp); 126 return newp; 127 } 128 129 int main() 130 { 131 int n, m; 132 int x, y, z, ans = 0; 133 scanf("%d%d", &n, &m); 134 135 for (int i = 1; i <= n; ++i) s[i] = 1, h[i] = i, ans ^= i; 136 while (m--) 137 { 138 char op[4]; 139 scanf("%s", op); 140 141 switch (op[0]) 142 { 143 case 'A': 144 { 145 scanf("%d%d", &x, &y); 146 147 Link(x, y); 148 149 split(x = geth(x), y = geth(y)); 150 z = push(y); 151 152 ans = ans ^ x ^ y ^ z; 153 h[x] = h[y] = h[z] = z; 154 break; 155 } 156 157 case 'Q': 158 { 159 scanf("%d", &x); 160 printf("%d\n", geth(x)); 161 break; 162 } 163 case 'X': 164 { 165 printf("%d\n", ans); 166 } 167 } 168 } 169 }
【SP2939 QTREE5】Query on a tree V(题目):
lsum[x]表示x所在的splay深度最浅的点到白点的距离,rsum[x]表示x所在的splay深度最深的点到白点的距离。询问时进行一次Access和Splay后,x就在当前splay的根且没有右儿子,相当于splay中深度最深的点,它的rsum就是它到白点的最短距离。修改时进行这两个操作后x没有父节点,直接修改即可。
维护子树信息时用一个multiset来维护,设当前节点的虚儿子为x,x因为与父节点连的边是虚边,而且x是父节点的虚儿子,所以在x所在的splay中x没有左儿子,所以x即为splay中深度最浅的点,所以lsum[x]便是x到白点的距离。每次Access时要把之前的实儿子变为虚儿子,要将之前的实儿子的lsum存入multiset,要将之前的虚儿子的lsum从multiset中删除。
ps:这里说的深度是将splay按中序遍历后得到的链的深度。

1 #include<cstdio> 2 #include<cstring> 3 #include<set> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 8 const int N = 1000010, INF = 2e9 + 7; 9 10 int n; 11 int fa[N], son[N][2], col[N]; 12 int size1[N], lsum[N], rsum[N]; 13 int h[N], num[N], nex[N], dqx; 14 15 multiset<int> s[N]; 16 17 bool no_root(int x) 18 { 19 return son[fa[x]][1] == x || son[fa[x]][0] == x; 20 } 21 22 int get(int x) 23 { 24 return (!s[x].empty()) ? (*s[x].begin()) : INF; 25 } 26 27 void pushup(int x) 28 { 29 if (!x) return; 30 31 int ls = son[x][0], rs = son[x][1]; 32 size1[x] = size1[ls] + size1[rs] + 1; 33 lsum[x] = min(lsum[ls], size1[ls] + min(col[x] ? 0 : INF, min(get(x), lsum[rs] + 1))); 34 rsum[x] = min(rsum[rs], size1[rs] + min(col[x] ? 0 : INF, min(get(x), rsum[ls] + 1))); 35 } 36 37 void rotate(int x) 38 { 39 int y = fa[x], z = fa[y], k = son[y][1] == x, w = son[x][!k]; 40 41 if (no_root(y)) son[z][son[z][1] == y] = x; 42 son[y][k] = w; 43 son[x][!k] = y; 44 if (w) fa[w] = y; 45 fa[x] = z; 46 fa[y] = x; 47 pushup(y); 48 } 49 50 void splay(int x) 51 { 52 while (no_root(x)) 53 { 54 int y = fa[x], z = fa[y]; 55 if (no_root(y)) rotate((son[y][1] == x) ^ (son[z][1] == y) ? x : y); 56 rotate(x); 57 } 58 pushup(x); 59 } 60 61 multiset<int> ::iterator it; 62 63 void Access(int x) 64 { 65 for (int y = 0; x; x = fa[y = x]) 66 { 67 splay(x); 68 s[x].insert(lsum[son[x][1]] + 1); 69 son[x][1] = y; 70 71 it = s[x].lower_bound(lsum[son[x][1]] + 1); 72 if ((it != s[x].end()) && (*it) == lsum[son[x][1]] + 1) s[x].erase(it); 73 pushup(x); 74 } 75 } 76 77 78 void add(int a, int b) 79 { 80 num[dqx] = b; 81 nex[dqx] = h[a]; 82 h[a] = dqx++; 83 } 84 85 void dfs(int u, int fath) 86 { 87 for (int i = h[u]; ~i; i = nex[i]) 88 { 89 int j = num[i]; 90 if (j == fath) continue; 91 92 s[u].insert(INF + 1); 93 fa[j] = u; 94 pushup(u); 95 dfs(j, u); 96 } 97 } 98 99 int main() 100 { 101 scanf("%d", &n); 102 103 lsum[0] = rsum[0] = INF; 104 105 memset(h, -1, sizeof(h)); 106 for (int i = 1; i < n; i++) 107 { 108 int x, y; 109 scanf("%d%d", &x, &y); 110 add(x, y), add(y, x); 111 } 112 113 dfs(1, 0); 114 115 int m; 116 scanf("%d", &m); 117 while (m--) 118 { 119 int op, x; 120 scanf("%d%d", &op, &x); 121 if (op) 122 { 123 Access(x); 124 splay(x); 125 printf("%d\n", rsum[x] > n ? -1 : rsum[x]); 126 } 127 else 128 { 129 Access(x); 130 splay(x); 131 col[x] ^= 1; 132 pushup(x); 133 } 134 } 135 }


