Codeforces Round #581 (Div. 2)-E. Natasha, Sasha and the Prefix Sums-动态规划+组合数学
Codeforces Round #581 (Div. 2)-E. Natasha, Sasha and the Prefix Sums-动态规划+组合数学
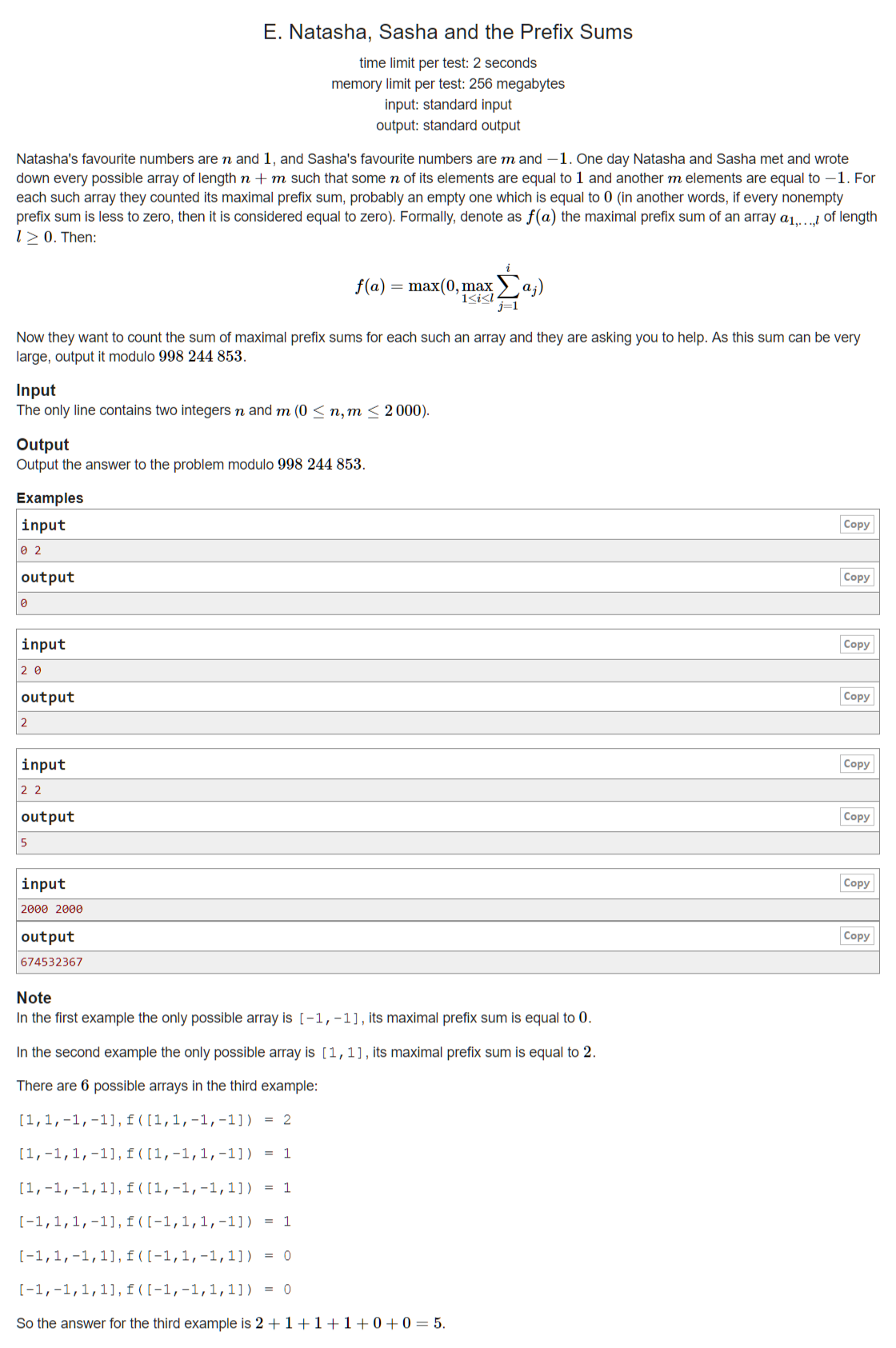
【Problem Description】
给你\(n\)个\(1\)，\(m\)个\(-1\)，他们任意排列有\(\frac{(n+m)!}{n!\cdot m!}\)中排列，每种排列都有一个最大前缀和（可能为\(0\)），求所有排列的最大前缀和之和为多少。
【Solution】
定义\(dp[i][j]\)表示有\(i\)个\(1\)，\(j\)个\(-1\)时所有排列的最大前缀和之和为\(dp[i][j]\)。则状态转移方程为：\(dp[i][j]=dp[i-1][j]+C_{i+j-1}^{j}+dp[i][j-1]-C_{i+j-1}^{i}+k[i][j]\)。其中\(k[i][j]\)表示有\(i\)个\(1\)，\(j\)个\(-1\)时最大前缀和为\(0\)的排列的个数。
其中\(dp[i-1][j]+C_{i+j-1}^j\)表示新增加一个数字\(1\)时，将其放到所有排列的最前端，则所有排列的最大前缀和都增加\(1\)，且总共有\(C_{i+j-1}^j\)种排列，所以在原来基础上增加了\(C_{i+j-1}^j\)。
\(dp[i][j-1]-C_{i+j-1}^i+k[i][j]\)表示新增加一个数字\(-1\)时，同上所有排列的最大前缀和减少\(1\)，除了最大前缀和为\(0\)的排列。
那为什么\(i-1\)个\(1\)，\(j\)个\(-1\)的所有排列个数为\(C_{i+j-1}^j\)呢？是因为根据多重集合的排列公式\(\frac{((i-1)+j)!}{(i-1)!\cdot j!}\)得到的。
最大前缀和\(k[i][j]\)怎么求呢？\(k[i][j]=k[i-1][j]+k[i][j-1]\)。表示在保证\(i\le j\)的情况下，新增加一个数字\(1\)，将其放到末端的排列数加上新增加一个\(-1\)，将其放在末端的排列数。
最后一个问题，为什么\(dp\)数组中\(1,-1\)要放在前端，\(k\)数组中\(1,-1\)要放在末端，并且为什么不能同时放在前端和后端以及任意其他位置？\(dp\)数组中放在前端是因为要求最大前缀和最大，比如将多出的\(1\)放在后端一定不可能使得最大前缀和最大，\(k\)数组中放在后端是因为要求最大前缀和为\(0\)，比如将多出的\(1\)放在前端，那么最大前缀和最小就等于\(1\)。
不能同时放在其他位置是因为只要放一个位置就包含了所有可能的排列，若同时放在其他位置就重复计算了可能出现的排列数。例如有\(i\)个\(1\)，\(j\)个\(-1\)，可知它们的所有排列个数为\(C_{i+j}^j\)，若有\(i-1\)个\(1\)，\(j\)个\(-1\)，则共有的排列个数为\(C_{i+j-1}^j\)，若有\(i\)个\(1\)，\(j\)个\(-1\)，则共有的排列个数为\(C_{i+j-1}^i=C_{i+j-1}^{j-1}\)。它们之间的关系就是：
由帕斯卡公式可知上式一定成立。所以可以知道由数组的含义决定了放在哪个位置，由上述关系决定了只能放\(1\)个位置。
【Code】
/*
* @Author: Simon
* @Date: 2019-08-28 19:32:35
* @Last Modified by: Simon
* @Last Modified time: 2019-08-28 20:26:23
*/
#include<bits/stdc++.h>
using namespace std;
typedef int Int;
#define int long long
#define INF 0x3f3f3f3f
#define maxn 2005
const int mod=998244853;
int dp[maxn][maxn]/*i个1，j个-1的所有排列的最大前缀和之和为dp[i][j]*/,k[maxn][maxn]/*i个1，j个-1的所有排列的最大前缀和为0的个数*/;
int bit[maxn<<1],C[maxn<<1][maxn<<1]/*组合数组*/;
Int main(){
#ifndef ONLINE_JUDGE
//freopen("input.in","r",stdin);
//freopen("output.out","w",stdout);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
int n,m;cin>>n>>m;
bit[0]=1;C[0][0]=1;
for(int i=1;i<=n+m;i++) bit[i]=bit[i-1]*i%mod,C[i][0]=1;
for(int i=1;i<=m;i++) k[0][i]=1;
for(int i=1;i<=n+m;i++){ //预处理
for(int j=1;j<=n+m;j++){
if(j>=i&&i<=n&&j<=m) k[i][j]=(k[i-1][j]+k[i][j-1])%mod;
if(i>=j) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}
for(int i=1;i<=n;i++) dp[i][0]=i;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=((dp[i-1][j]+C[i+j-1][j]+dp[i][j-1]-C[i+j-1][i]+k[i][j-1])%mod+mod)%mod;
}
}
cout<<(dp[n][m]+mod)%mod<<endl;
#ifndef ONLINE_JUDGE
cout<<endl;system("pause");
#endif
return 0;
}
