RSA算法及数学基础
RSA算法及数学基础
1. 公钥体制数学基础
由于传统密钥体制出现了困难,例如2000个用户保密通信每个人需要保存1999个密钥(两两保密通信需要共(2000*19999)/2 = 1999000个密钥,每人保管1999个),在密钥管理分配上有困难。另外由于数字签名(身份认证)的需要增加。
公钥体制解决了上述两个问题,即每个人有一对密钥(公钥和私钥),将公钥公开,私钥自己保管,这样每人只要保管好自己的私钥就可以了。通信时使用收信方的公钥进行加密,收信方使用私钥进行解密。在身份认证时,签名者使用私钥签名,验证签名者使用签名者的公钥验签。当然在实际应用时还有其他的问题需要保证,例如抗抵赖,保持信息的完整性等密码学问题。在本文中先不考虑。
有上述公钥体制的任务中我们知道,区别于其他密钥体制算法,公钥算法需要做到的是将加密密钥(公钥)和加密算法公开,破坏者也不能由公钥和密文破译出明文。只有使用解密密钥(私钥)和解密算法才能解出明文。而且保证通过公钥不能推出私钥。
上述内容可以通过所谓的“单向函数”来实现。(传统的密钥体制中加密算法和解密算法是互逆的。)所谓“单向函数”是指加密函数E和解密函数D。但是已知加密函数E推导其逆运算却非常困难(也就是推导私钥的过程)。所以若不知道解密函数(或私钥)不可能解出明文。
单向函数的实现依赖的是大整数因子分解的难度,根据
算数基本定理:任何大于1的整数都可以分解成素数乘积的形式,并且,如果不计分解式中素数的次序,该分解式是唯一的[微软中国1] 。
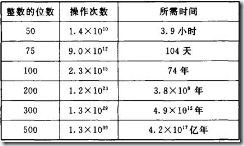
这个定理在理论上十分漂亮,但是操作起来却非常困难下表列出了现代最快的分解算法在大型计算机上分解一个大数所用的时间。
2. RSA相关的数论知识
1. 一个大于1的整数p,若除1和起本身之外没有其他正整数因数(约数),称P为素数。
2. 若整数a和b最大公约数为1,则称a,b互素,记为(gcd(a,b)= 1)。
3. 设n为正整数,a和b为整数,若a和b被n除后所得余数相同,称a和b模n同余,记为a≡b(mod n)。此式被称为同余式。若n能整除a则同余式表示为a≡0(mod n)。
两个整数模n同余的等价说法有:a和b被n除余数相同。a-b被n整除。a和b在模n的同一个剩余类中。存在整数s使得a=sn+b。
4. 同余式的一些运算性质,
(1) 若a≡b(mod n),c≡d(mod n)则有ac≡bd(mod n)。特别的有,ka≡kb(mod n),k为任意整数。
(2) 若a≡b(mod n),d是a,b,n的公因数,则(a/d) ≡(b/d)(mod n/d)。特别的有an≡bn(mod n),n为正整数。[微软中国2]
(3) 若ka≡kb(mod n),且k与n互素时,有a≡b(mod n)。(同余式消去律)
5. 设n为正整数 ,则任何一个整数被n除 ,余数必为0,1,2,…,n-1中的某一个,把整数集中被n除余数相同的数分别归为一类,记为[0],[1],[2]…,[n-1],这样就按模是否同余把整数集分成n类,其中每一类都称为模n的一个剩余类。显然,每个整数必属于上述类中的一类,被n除余数不同的数必属于上述的不同类中。若a0,a1,a3…,an-1分别取自上述类的不同类中,称a0,a1,a3…,an-1为模n的一个完全剩余系,该剩余系中的数两两模n不同余。
6. 含有未知量的同余式称为同余方程。一次同余方程是最简单的一种,其一般形式为ax≡b(mod n)。若a,n的最大公约数d能整除b,则ax≡b(mod n)有解。且恰有d个解。若a,n的最大公约数d不能能整除b,则ax≡b(mod n)无解。例如同余方程7x≡1(mod 5)。7与5最大公约数为1,能被b=1整除,故有一个解。7x≡1(mod 5)≡6≡11≡21(mod5)。由于7与5互素有消去律得x=3。.[微软中国3]
一般地 解同余方程的步骤为 ①判断解的情况 ②当同余方程的a,b,n有公因数时 ,约去公因数化简方程 ③利用同余的定义和消去律求方程的解。
7. 费马小定理:设任意整数a和素数p互素[微软中国4] ,则ap-1 ≡1(mod p)。
8. 欧拉定理:若n,a为正整数,且n,a互质,(a,n) = 1,则a^φ(n) ≡ 1 (mod n)。
9. 模运算极其性质:
基本概念:
给定一个正整数p,任意一个整数n,一定存在等式 n = kp + r ;
其中k、r是整数,且 0 ≤ r < p,称呼k为n除以p的商,r为n除以p的余数。
对于正整数p和整数a,b,定义如下运算:
取模运算:a % p(或a mod p),表示a除以p的余数。
模p加法:(a + b) % p ,其结果是a+b算术和除以p的余数,也就是说,(a+b) = kp +r,则(a + b) % p = r。
模p减法:(a-b) % p ,其结果是a-b算术差除以p的余数。
模p乘法:(a * b) % p,其结果是 a * b算术乘法除以p的余数。
说明:
1. 同余式:正整数a,b对p取模,它们的余数相同,记做 a ≡ b % p或者a ≡ b (mod p)。
2. n % p得到结果的正负由被除数n决定,与p无关。例如:7%4 = 3, -7%4 = -3, 7%-4 = 3, -7%-4 = -3。
(1)若p|(a-b),则a≡b (% p)。例如 11 ≡ 4 (% 7), 18 ≡ 4(% 7)
(2)(a % p)=(b % p)意味a≡b (% p)
(3)对称性:a≡b (% p)等价于b≡a (% p)
(4)传递性:若a≡b (% p)且b≡c (% p) ,则a≡c (% p)
模运算与基本四则运算有些相似,但是除法例外。其规则如下:
(a + b) % p = (a % p + b % p) % p (1)
(a - b) % p = (a % p - b % p) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
(a^b) % p = ((a % p)^b) % p (4)
结合率: ((a+b) % p + c) % p = (a + (b+c) % p) % p (5)
((a*b) % p * c)% p = (a * (b*c) % p) % p (6)
交换率: (a + b) % p = (b+a) % p (7)
(a * b) % p = (b * a) % p (8)
分配率: ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p (9)
重要定理
若a≡b (% p),则对于任意的c,都有(a + c) ≡ (b + c) (%p);(10)
若a≡b (% p),则对于任意的c,都有(a * c) ≡ (b * c) (%p);(11)
若a≡b (% p),c≡d (% p),则 (a + c) ≡ (b + d) (%p),(a - c) ≡ (b - d) (%p),
(a * c) ≡ (b * d) (%p),(a / c) ≡ (b / d) (%p); (12)
若a≡b (% p),则对于任意的c,都有ac≡ bc (%p); (13)
3. RSA算法及证明:
1. RSA定理证明:
定理:设p,q是不同的素数,n=pq记φ(n)=(p-1)(q-1),如果e,d是与φ(n)互素[微软中国5] 的两个正整数(e,d<φ(n)),并满足ed≡1(mod φ(n)),则对于每个整数x,都有xed≡x(mod n)。
分析:为了证明xed≡x(mod n),只要证明φ(n)是xed-x的因数即可。又因为n=pq,而p,q都是素数,故只要证明p和q都是xed-x的因数即可[微软中国6] ,即
xed≡x(mod p) (1)
xed≡x(mod q) (2)
证明:证明式1,若p是x的因数则式1必然成立
若p不是x的因数,则由ed≡1(mod φ(n))得ed-1=k(p-1)(q-1),k为任意整数。则xed=xk(p-1)(q-1)+1 = x*(xp-1)k(q-1)
根据费马小定理因为x与p互素所以xp-1≡1(mod p)
所以xed≡x*(1)k(q-1) ≡x(mod p)[微软中国7]
同理可证xed≡x(mod q)
2. RSA定理与RSA加密算法:
RSA加密算法为:
(1) 取两个大素数p,q (保密);
(2) 计算 n=p*q (公开), φ(n)=(p-1)*(q-1) (保密);
(3) 随机选取整数e,满足 gcd(e, φ(n))=1 (e与φ(n)互素)(公开);
(4) 计算 d 满足 d*e≡1 (mod φ(n)) (保密);
(5) {e,n}为公钥,{d,n}为私钥,也可以用{e,d}表示密钥对
(6) 加密时c = xe mod n ;解密时 x = cd mod n
(7) 签名时c = xd mod n ;解密时 x = ce mod n
问题:为什么xed≡x(mod n) 就能保证(6)和(7)正确?
分析:解xed≡x(mod n)同余式方程,该方程可能有n个解[微软中国8] ,这n个解都在模n的同一个剩余类中,小于n的解只有一个,由于明文小于n[微软中国9] ,则该解即是明文x。而xed mod n得到的就是小于n的那个解。
另外,注意密文c并不等于xe而是c≡xe(mod n)。这里有上一段中我们知道要想求出明文x,解同余式方程xed≡x(mod n)可得,这时只要等式左边的数与X同余就能得到正确的明文。由于c≡xe(mod n),所以可得cd≡xed(mod n),所以cd≡xe(mod n)。
3. 从另一个角度解释为什么RSA加密和解密过程是互逆的:
将问题改为证明:A^e mod n = B^(e*d)mod n-----------1
即B^(e*d)mod n = B
其中A为密文,B为明文。
证明:因为ed+1=(p-1)(q-1)所以B^(e*d)=B^(k(p-1)(q-1)+1),
当B与n互素时,根据欧拉定理有:
B^(k(p-1)(q-1)+1) mod n
= B*B^ k(p-1)(q-1) mod n
= (B mod n )*((B^(p-1)(q-1))^k mod n)
= (B mod n ) * (((B^(p-1)(q-1)) mod n) ^ k ) mod n)
= B * (1^k mod n)
=B[微软中国10]
当B与n不互素时,由于n=p*q,B必然能被p或者q整除,假设B=k*p[微软中国11] ,则B与q互素。再运用费马定理有:
B^(q-1) = 1 mod q,
则(B^(q-1))^(p-1)K = 1^(p-1)K mod q = 1 mod q,
即B^k(p-1)(q-1) mod q =1。
两边同时乘以B,得到
B^(k(p-1)(q-1)+1) mod q = B
也就是B^(e*d)mod n = B
4. RSA算法举例:
公钥体制中,单向函数的构造基于大整数n因数分解的困难 ,因而n的两个因数p与q都应取大素数。为便于理解,我们选取两个较小的素数来说明该体制的实施。
例:给定两个素数p=13,q=17
(1)为用户A和B设计公钥和私钥。
(2)用户A将明文x=3 加密。
(3)用户A将明文x=3 加密并签名后发给B,B解密并验证签名试把加密通信过程详细写出。
解:(1)计算得n=p*q=221,φ(n)=(p-1)*(q-1)=12*16=192。
随机选取与φ(n)=192互素的两个数e1=7和e2=13,并建立同余方程
7x≡1(mod 192)
13x≡1(mod 192)
由于7和192;13和192都互素,7x ≡1 ≡ 193 ≡ 385 mod 192,根据消去律得到x = 55即d1=55,同理得到d2 =133.
将密钥{7,55}和{13.133}交给A和B两个人。将n,e1,e2公开,d1,d2交给A和B各自秘密保管。φ(n)=192由密钥制作者保管。
(2)A在公钥簿上查询到B的公钥e2=13,得到加密函数
E2(x) ≡ x^13 (mod 221),对信息x=3进行加密得到密文y≡ 3^13 (mod 221)
因为3^2≡9(mod 221);3^4≡9*9≡81(mod 221);3^8≡81*81≡6561≡152(mod 221)[微软中国12]
所以,3^13 ≡ 3^(8+4+1) ≡152*81*3 ≡ 29 (mod 221)
A将密文29发出给B。
B使用自己的私钥133进行解密x = D2(y)≡ y^133 ≡ 29^133(mod 221). 用上述方法计算得29^4 ≡ 81 (mod 221); 29^128 ≡ 35 (mod 221);所以,29^133 ≡ 29^(128+4+1) ≡ 35*81*29 ≡ 3 (mod 221)。
B得到明文3。
计算得z=211。
B得到密文后,先查到A的公钥7,用7解密密文z=211,得到y。在使用自己的私钥对y进行验证得到信息x=3。[微软中国13]
[微软中国1]分解式中因数的个数是固定的吗?
是,因为素数不能再分了。即使已知一个大数能分成俩个素数的乘积(已知因数个数)其分解仍然很难吗?
[微软中国2]自己想的
[微软中国3]同余方程中若a与n互素则方程必有且只有一个解,这也是RSA加解密函数中使用的。
[微软中国4]即使两个和数也可以互素例如8和27
[微软中国5]为什么e要与φ(n)互素?因为只有e和φ(n)互素了,同余方程ed≡1(mod φ(n))才有且仅有一个解。
[微软中国6]两个数的最小公倍数=p*q/两个数的最大公约数,若两个数互素(不一定非得全是素数)则两数最大公约数为1,即互素的两个数的最小公倍数就是这两个数的积。而两个数的公倍数都是其最小公倍数的倍数。所以n=pq是p和q的最小公倍数,而只要证明xed-x是p和q的公倍数(即q和p都是xed-x的因数)就可以证明n是xed-x的因数。
前提是xed-x > n???
[微软中国7]根据上述同余式的运算性质(2):
因为xp-1≡1(mod p),
所以(xp-1)k(q-1) ≡1(mod p)
根据同余式的运算性质(1):
所以x*(xp-1)k(q-1)≡x(mod p)
[微软中国8]为什么必有解?因为a是b的倍数?因为未知数本身就是模n的剩余类,而模n的剩余类肯定是存在的。
[微软中国9]注意明文必须小于n。
[微软中国10]参考模运算规则。
[微软中国11]Why?
[微软中国12]与直接求3^13不同
[微软中国13]先签名在加密。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号