[文档].艾米电子 - 算术运算电路，Verilog

对读者的假设

已经掌握：

内容

1 算术电路

Verilog HDL中，+、-、*、/、%都是可以综合的，其消耗的资源视器件资源不同而不同。譬如：+、-都会被综合成Adder，每一位大约消耗一个LE（Cyclone II）；*则会被综合成乘法器，若器件内含有乘法器，则底层被映射成乘法器，否则使用LE实现。下面慢慢讨论。

1.1 加法运算 +

代码1.1 加法运算（可综合）

module arithmetic(
  input  [7 :0] iA,
  input  [7 :0] iB,
  output [8 :0] oAdd 
);
assign oAdd = iA + iB;
endmodule

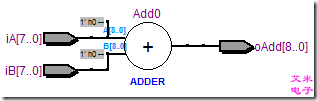
图1.1 加法运算综合的RTL视图及资源消耗

如图1.1 所示加法运算被综合成ADDER，其资源消耗约1 LE/位（对应Cyclone II的LUT-4结构的LE）。

代码1.2 加法运算的testbench（不可综合，仅用于仿真）

`timescale 1ns/1ns
module arithmetic_tb;
reg [7:0] i_a = 8'b1011_0111;
reg [7:0] i_b = 8'b0100_1000;

wire [8:0] o_add;

initial #100 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iB   (i_b),    
  .oAdd (o_add)   
);

endmodule

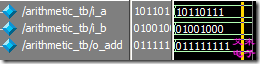
图1.2 加法运算的功能仿真

1.2 乘法运算 *

代码1.3 乘法运算代码

module arithmetic(
  input  [7:0] iA,
  input  [7:0] iB,
  output [15:0] oMul 
);
assign oMul = iA * iB;
endmodule

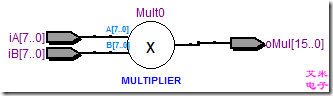
图1.3 乘法运算直接调用lpm_mult

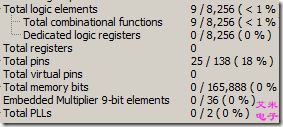
图1.4 乘法运算综合的RTL视图及资源消耗

观察综合后的结果，我们发现，Cylone II的x被直接映射到了乘法器。此处为Embedded Multiplier 9-bit elements，实际上Cyclone II嵌入的乘法器为18位的，每一个乘法器又可以拆成2个9位的乘法器使用。

代码1.4 乘法运算的testbench

`timescale 1ns/1ns
module arithmetic_tb;
reg [7:0] i_a = 8'b1011_0111;
reg [7:0] i_b = 8'b0100_1000;

wire [15:0] o_mul;

initial #100 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iB   (i_b),    
  .oMul (o_mul)   
);

endmodule

图1.5 乘法运算的功能仿真波形

1.3 除法运算 /

代码1.5 除法运算

module arithmetic(
  input  [7:0] iA,
  input  [7:0] iB,
  output [7:0] oDiv 
);
assign oDiv = iA / iB;
endmodule

综合之后，我们发现除法运算是直接调用的lpm_divide来实现的。

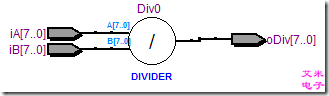
图1.5 除法运算直接调用lpm_divide

图1.6 除法运算综合的RTL视图及资源消耗

由图1.6所示，除法运算虽然可以直接调用宏，但是其资源消耗也是非常巨大，大约每一位除法消耗10个LE。

代码1.6 除法运算的testbench

`timescale 1ns/1ns
module arithmetic_tb;
reg [7:0] i_a = 8'b1011_0111;
reg [7:0] i_b = 8'b0100_1000;

wire [7:0] o_div;

initial #100 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iB   (i_b),    
  .oDiv (o_div)   
);

endmodule

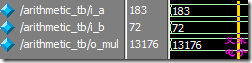
图1.7 除法运算的功能仿真波形

1.4 取余运算 %

代码1.7 取余运算

module arithmetic(
  input  [7:0] iA,
  input  [7:0] iB,
  output [7:0] oMod 
);
assign oMod = iA % iB;
endmodule

同除法运算一样，取余运算也是直接调用的lpm_divide来实现的。

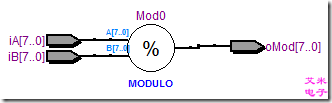
图1.8 取余运算直接调用宏实现

图1.9 取余运算综合的RTL视图及资源消耗

代码1.8 取余运算的testbench

`timescale 1ns/1ns
module arithmetic_tb;
reg [7:0] i_a = 8'b1011_0111;
reg [7:0] i_b = 8'b0100_1000;

wire [7:0] o_mod;

initial #100 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iB   (i_b),    
  .oMod (o_mod)   
);

endmodule

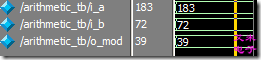
图1.10 取余运算的功能仿真波形

2 数据比较器

代码2.1 数据比较器（可综合）

module arithmetic(
  input [3:0] iA,
  input [3:0] iB,
  output oEQ,       // 等于
  output oNEQ,      // 不等于
  output oGT,       // 大于
  output oGT_EQ,    // 大于等于
  output oLT,       // 小于
  output oLT_EQ     // 小于等于
);

assign oEQ    = (iA == iB),
       oNEQ   = (iA != iB),
       oGT    = (iA >  iB),
       oGT_EQ = (iA >= iB),
       oLT    = (iA <  iB),
       oLT_EQ = (iA <= iB);

endmodule

观察第12~17行，数据比较器的描述方法与C语言非常一致。

assign oEQ    = (iA == iB),
       oNEQ   = (iA != iB),
       oGT    = (iA >  iB),
       oGT_EQ = (iA >= iB),
       oLT    = (iA <  iB),
       oLT_EQ = (iA <= iB);

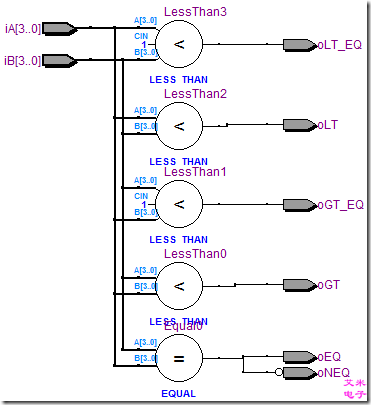
图2.1 综合后的数据比较器的RTL视图

代码2.2 数据比较器的testbench（不可综合，仅用于仿真）

`timescale 1ns/1ns
module arithmetic_tb;
reg [3:0] i_a;
reg [3:0] i_b;
wire o_eq,
     o_neq,
     o_gt,
     o_gt_eq,
     o_lt,
     o_lt_eq;

initial begin
  i_a = 5;
  i_b = 5;
  #20 i_a = 6;
  #20 i_a = 4;
  #20 $stop;
end

arithmetic arithmetic_inst(
  .iA     (i_a),
  .iB     (i_b),
  .oEQ    (o_eq),       
  .oNEQ   (o_neq),      
  .oGT    (o_gt),       
  .oGT_EQ (o_gt_eq),    
  .oLT    (o_lt),       
  .oLT_EQ (o_lt_eq)     
);

endmodule

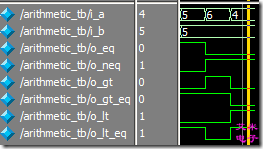
图2.2 数据比较器的功能仿真波形

3 移位运算

Veirlog HDL 2001支持逻辑移位及算术移位。

3.1 逻辑移位

代码3.1 逻辑移位（可综合）

module arithmetic(
  input [7:0] iA,
  input  [2:0] iBit,    // 移位的位数 0~7
  output [7:0] oSLL,    // 逻辑左移
  output [7:0] oSRL     // 逻辑右移
); 

assign oSLL = (iA << iBit),
       oSRL = (iA >> iBit); 

endmodule

第8~9行，逻辑移位的符号和C语言也是一致的：>>（逻辑右移，shift right logical）；<<（逻辑左移，shift left logical）。assign关键字后，若有多条语句，则可以使用逗号隔开；也可以分开使用两个assign语句来描述。

assign oSLL = (iA << iBit),
       oSRL = (iA >> iBit);

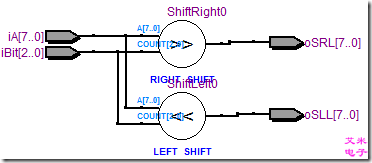
图3.1 逻辑移位的RTL视图

代码3.2 逻辑移位的testbench

`timescale 1ns/1ns
module arithmetic_tb;
reg [7:0] i_a = 8'b1011_0111;
reg [2:0] i_bit = 0;

wire [7:0] o_sll,
           o_srl;

initial while(i_bit<7) #20 i_bit = i_bit + 1'b1;
initial #160 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iBit (i_bit),    
  .oSLL (o_sll),    
  .oSRL (o_srl)    
);

endmodule

第3~4行，在声明reg类型的信号时，同时赋初值。

reg [7:0] i_a = 8'b1011_0111;
reg [2:0] i_bit = 0;

第6~7行，同一类型及等位宽的信号，可以使用逗号隔开声明，也可以分开声明。

wire [7:0] o_sll,
           o_srl;

第9行，采用while语句来生成激励，其用法与C语言一致。

initial while(i_bit<7) #20 i_bit = i_bit + 1'b1;

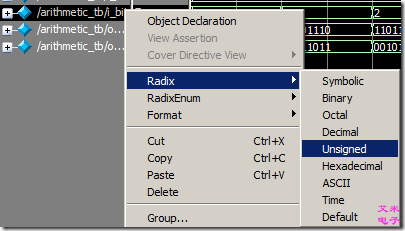
右键所需观察的信号，选择Radix>Unsigned，以无符号十进制形式查看i_bit。如图3.2所示。

图3.2 以无符号十进制形式查看i_bit

图3.3 逻辑移位的功能仿真波形

3.2 算术移位

算术移位与逻辑移位的区别见参考3。

代码3.3 有符号数的逻辑移位与算术移位（可综合）

module arithmetic(
  input signed [7:0] iA,
  input  [2:0] iBit,        // 移位的位数 0~7
  output signed [7:0] oSLL, // 逻辑左移
  output signed [7:0] oSRL, // 逻辑右移
  output signed [7:0] oASL, // 算术左移
  output signed [7:0] oASR  // 算术右移
); 

assign oSLL = (iA <<  iBit),
       oSRL = (iA >>  iBit),
       oASL = (iA <<< iBit),
       oASR = (iA >>> iBit);

endmodule

第2~7行，移位的位数被声明成无符号数，而移位的数据及其结果被声明成有符号数。

  input signed [7:0] iA,
  input  [2:0] iBit,        // 移位的位数 0~7
  output signed [7:0] oSLL, // 逻辑左移
  output signed [7:0] oSRL, // 逻辑右移
  output signed [7:0] oASL, // 算术左移
  output signed [7:0] oASR  // 算术右移

第10~13行，与逻辑移位不同，算术移位的运算符是：<<<（算术左移，arithmetic shift left）；>>>（算术右移，arithmetic shift right）。

assign oSLL = (iA <<  iBit),
       oSRL = (iA >>  iBit),
       oASL = (iA <<< iBit),
       oASR = (iA >>> iBit);

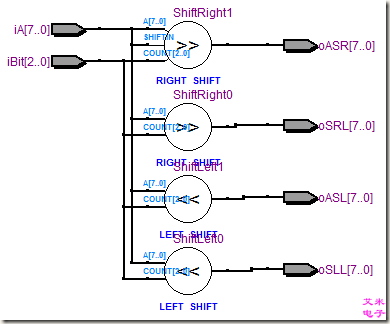
图3.4 有符号数的逻辑移位与算术移位的RTL视图

代码3.4 有符号数的逻辑移位与算术移位的testbench（不可综合，仅用于仿真）

`timescale 1ns/1ns
module arithmetic_tb;
reg signed [7:0] i_a = 8'sb1011_0111;
reg signed [2:0] i_bit = 0;

wire signed [7:0] o_sll,
                  o_srl,
                  o_asl,
                  o_asr;

initial while(i_bit<7) #20 i_bit = i_bit + 1'b1;
initial #160 $stop;

arithmetic arithmetic_inst(
  .iA   (i_a),
  .iBit (i_bit),    
  .oSLL (o_sll),    
  .oSRL (o_srl),
  .oASL (o_asl),
  .oASR (o_asr)   
);

endmodule

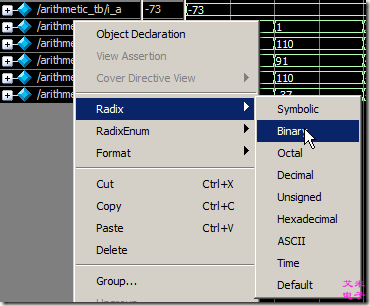
全选所有信号，右键选择Radix>Binary，以二进制形式查看。如图3.5所示。