数据挖掘经典算法——最大期望算法

算法定义

      最大期望算法（Exception Maximization Algorithm，后文简称EM算法）是一种启发式的迭代算法，用于实现用样本对含有隐变量的模型的参数做极大似然估计。已知的概率模型内部存在隐含的变量，导致了不能直接用极大似然法来估计参数，EM算法就是通过迭代逼近的方式用实际的值带入求解模型内部参数的算法。

算法描述

      算法的形式如下：

随机对参数赋予初值；

    While(求解参数不稳定){

       E步骤：求在当前参数值和样本下的期望函数Q；

       M步骤：利用期望函数重新计算模型中新的估计值；

}

      上面的伪代码形式可能过于抽象，就结合一个实际的例子来说明。

      例子：存在3枚硬币A,B和C，抛出正面的概率是π,p和q。进行如下抛硬币的试验：先抛硬币A，如果A是正面则需要抛硬币B，否则就抛硬币C。如果B或C是正面结果为1，否则结果为0；独立进行n次试验。取n = 10，得到的观测结果如下：

                            1,1,0,1,0,0,1,0,1,1

      每一枚硬币的分布都是一个二项分布，而A,B,C三个硬币对应的事件之间又潜在有某种联系。用Y表示观测变量，对于第i次观测结果的值记作y_i，用向量θ来表示整个模型中的未知参数π,p和q，则整个三币模型的概率可以表示为：

                              

      如果采用最大似然估计法来求解公式(1)，以此来估计模型中的参数，即求解下式：

                              

        由于公式(1)内部包含了+号，很难直接求偏导求解得到参数的估计值。必须寻求其他的办法解决这个问题，现引入一个隐含变量Z表示在试验中抛掷A硬币的结果（1代表正面，0代表反面），就可以将原先的似然函数转换成下式：

                           

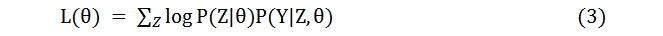
         我们给出E步骤中期望函数Q的定义如下，具体的证明会放到下一节：

                                 

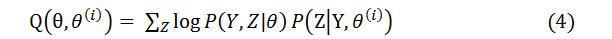
对于上面的例子， P(Z|Y, θ⁽ⁱ⁾) =(zπp^y(1-p)^1-y + (1-z)(1-π)q^y(1-q)^1-y)/ P(Y|θ)，上式中没有未知的参数（Z的值在每次累加时被确定），所以可以直接算出具体的值。将计算出的结果带入(4)式我们就得到了期望函数。

         在M步骤中，分别对θ向量的每一个分量求其偏导，另偏导数的值等于零求出极大值得到新的参数估计值，重复以上两个步骤，直到收敛。

 理论与推导

       在推导EM算法之前，有一些基本的数学概念需要重新梳理一下，以便可以透彻得理解EM算法。

     a) 极大似然估计

　　极大似然估计是最常用的一种点估计方法，极大似然估计基于的一个直观想法就是“概率最大的事件最有可能出现”。假设有一系列事件A1,A2,…,An被观测到发生了，且事件Ai发生的概率为pi，就有理由相信事件序列A1,A2,…,An的理论概率是最大的，所以有max pi(1<=i<=n)，以此可以估计出概率模型中参数。

　　利用极大似然估计方法进行参数估计，必须知道总体的概率分布类型。构造一个似然函数，将样本的观察值带入似然函数，对某一个参数求偏导数另其为零，算出极值点的参数值就是估计得到的参数结果，用θ表示需要估计的参数向量，x_i表示第i个样本的观测结果，似然函数的形式可以是：

 　　　　　　　　　　　　　　　　　　　　

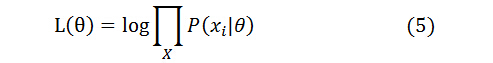
　　b) Jessen不等式

　　Jessen不等式的形式如下：

　　f(E(X)) ≥ E[f(x)]，当函数f(x)是一个凹函数时成立，且等号只有满足对于任意x，都有E(X) = x时取到。

　　要理解Jessen不等式，可以参考下图。在图中曲线f(x)上取任意两点x,y，有不等式f(1/2(x+y))≥ 1/2[f(x) + f(y)]恒成立，将这个不等式推广到多维向量且考虑向量分布不均匀的情况，不等式左边就是f(E(X))，右边就是E(f(x))。

　　

　　c) 最大下界函数

　　　要用极大似然估计方法来确定模型中的参数，就是要计算在似然函数L(θ)最大化的时候对应的参数的值，上一节中已经提过对于含有隐含变量的模型，直接通过求偏导数的方法来确定似然函数的极大值是很困难的。在EM算法的求解过程中，每一次迭代构造了一个新的下界函数，最大化这个下界函数来逼近实际的似然函数，求解得到一个局部最优的极值。

　　　假设在EM算法的求解过程中，经过第i次迭代后得到的参数向量为θ⁽ⁱ⁾，这里我们以这组参数值作为观测点，以此估计隐含变量的概率分布；将这个分布带入似然函数的公式得到近似的L(θ⁽ⁱ⁾)，考虑真实的似然函数与近似似然函数之间的差值：

　　　　　　　　　　　　

　　　　　　　　　　

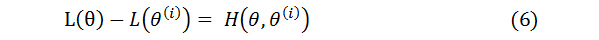
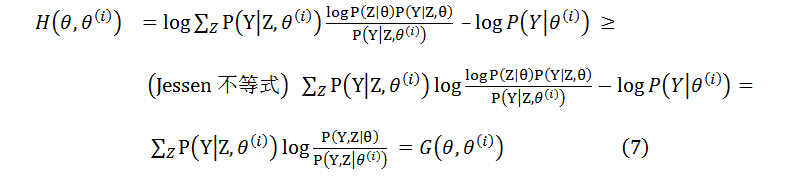
　　　　由(6)和(7)可以构造似然函数的一个下界函数B(θ, θ⁽ⁱ⁾)，有如下结论：

　　　　　　　　　　　　　　　　  

现在仔细回忆一下，模型中的参数之所以难以直接求解的根本原因是：在这一类问题中，实际上存在两类参数，一类是模型自带的参数向量θ，第二类是受这个参数影响的隐藏变量Z。在EM算法的第i次迭代的过程中，利用θ⁽ⁱ⁾构造了隐含变量Z的分布有效得消除了Z对结果的影响，同时根据Jessen不等式的性质，我们也能够保证构造的下界函数与似然函数之间必然有交点，且始终处于了似然函数图像的下方。

总结EM算法的E步骤，包含了如下几个操作：

1. 1. 将当前轮次得到的参数θ⁽ⁱ⁾作为固定的观测点；
   2. 利用参数θ⁽ⁱ⁾计算出隐含变量Z的分布；
   3. 将隐含变量Z的分布带入构造似然函数在当前观测点下的下界函数；

　　之后再M步骤中，通过极大化下界函数得到一组新的参数向量θ⁽ⁱ⁺¹⁾，如此循环既可以求出似然函数的一个局部最优。用一幅图像更直观得展现这第i次迭代的过程：

 

 

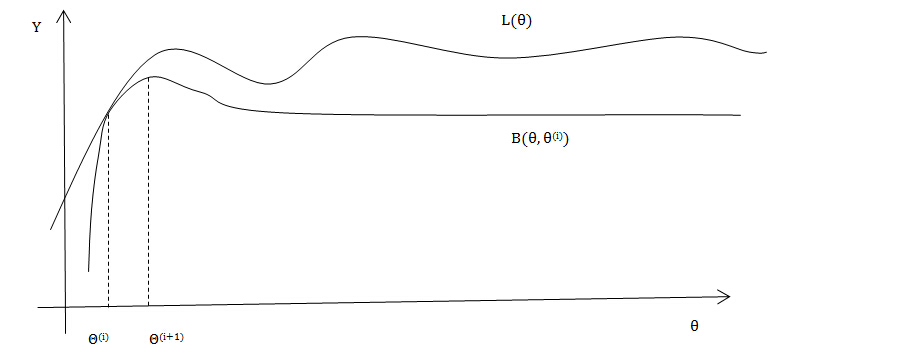
　　由公式(8)可知，下界函数由两个部分组成，在参数θ⁽ⁱ⁾确定的条件下，L(θ⁽ⁱ⁾)就是一个常量，极大化下界函数等价于极大化公式(7)中的G(θ,θ⁽ⁱ⁾)，同时将G(θ,θ⁽ⁱ⁾)在log内部的对求极大值没有影响的常量部分P(Y,Z|θ⁽ⁱ⁾)，即证最大化下界函数等价于证明公式(4)中的Q(θ,θ⁽ⁱ⁾)。

　　补充几点关于EM算法的细节，从图中也可以清晰得看出：

　　a) EM算法是一种初始值敏感的算法，选取不同初始参数会有不同的最终结果；

　　b) EM算法得到的不会是全局最优，每次迭代逼近的都是当前的局部最优。

　　d)算法的收敛性

　　　　　　之前已经证明了可以通过定点参数值估计隐含变量的分布，并以此来构造下界函数，通过极大化下界函数来逼近似然函数的极大值。要证明EM算法的合理性，还有一个关键点就是，是不是每一次迭代都必定能比之前更优，即证明算法的收敛性。

　　　　　

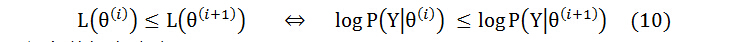
　　　　　　已知条件概率公式：

　　　　　

　　　　　　将公式(11) 带入(10)中并且在两边同时乘以P(Z|Y, θ⁽ⁱ⁾)，可以得到下式：

　　　　

　　　　　　解释一下上面的公式，第一个不等号是调用了Jessen不等式，在EM算法M步骤中θ⁽ⁱ⁺¹⁾是使Q(θ,θ⁽ⁱ⁾)取极大值的参数，所以φ必定是大于等于零的值。

参考资料

[1].     《统计学习方法》李航

[2].     https://www.coursera.org/course/ml

[3].     http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

[4].     http://www.cnblogs.com/mindpuzzle/archive/2013/04/05/2998746.html

后记

　　　整理完成这篇文章前前后后花了本人接近半个月的时间（各期间种杂事，还生病静养了好几天），写得也是断断续续，但是总算是基本完成了。EM算法虽然看似结构简单，但是其证明和内部的数学原理理解起来还是相对有些难度的。期间找了相当多的资料进行参考，发现很多文章里都夹杂了过多复杂的公式，看着也很头疼。在整理的过程中，我也尽量的避免大范围得套用数学数学公式。