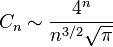组合数学

1. 全排列的数目是n ！，当 n=10 时， n ！ =3628800 ，接近穷举极限。

2. N个元素的子集为 2^n ，非空子集为 2^n-1 ，非空真子集为 2^n-2 ，当 n=20 时， 2^n=1048576 接近穷举极限。

3. 研究若干可重复元素所组成的序列。假设有m 种元素，则有 m^n 个长度为 n 的序列（也就是每个位置上有 m 种取法，共 n 个位置），另外，长度为 n 的二元串（也就是只包含两种不同字符）的个数等于 n 个不同元素的子集数目（每个位置有 2 种取法，所以有 2^n ，根据上一条，显然等于个数为 n 个的不同元素的子集数目）

 

一、 二项式系数

1. 从n 个人中选出 k 个人答案为 C(n,k)

2. 穿越网格的路径数：从一个n*m 的网格的左上角走到右下角，很显然要走 n+m 步， n 次往下， m 次往右，从中选择 n 步往下，所以是 C(n+m,n) ，同理，也可以从中选择 m 步往右，因此有 C(n+m,m)=C(n+m,n) 可得 C(n,k)=C(n,n-k) 。

3. 顾名思义，二项式系数即为(a+b)^n 的系数，同样意义为从 n 个因子中选择 k 个因子 a 的方案数，为 C(n,k) 。

4. 杨辉三角。该表为二项式系数，第(n+1) 行第 i 个数为 C(n,i) 的值。另外，第 (n+1) 行之和为 2^n ，也就是说 C(n,0)+C(n,1)+...+C(n,n)=2^n 。另外很显然在杨辉三角中，一个数是由上两个数相加得到（非边界情况），所以有公式 C(n,k)=C(n-1,k-1)+C(n-1,k) ，有效预防用阶乘相除溢出的情况（ ps ： C(n,k)=n!/[(n-k)!k!] ），然后边界为 C(n,0)=C(n,n)=1 。代码如下（递归函数）：

int C(int n,int k)

{

if (n==k || n==0) return 1;

return C(n-1,k)+C(n-1,k-1);

}

同样可以用递推写

for (i=0;i<=n;i++)

{

for (j=0;j<=i;j++)

{

if (j==0 || i==j) c[i][j]=1;

else c[i][j]=c[i-1][j]+c[i-1][j-1];

}

}

二、 斐波那契数列（兔子问题……）

1. 递推公式：Fn=Fn-1+Fn-2,F0=0,F1=1

2. 封闭形式： F(n)=(1/√5)*{[(1+√5)/2]^(n+1) - [(1-√5)/2]^(n+1)}。 （误差正负 1 ）

3. 楼梯问题：一段楼梯有n 级台阶，一次只能跨 1-2 级，问有多少种走法。要么跨一级，也就是 Fn-1 种，要么跨两级 Fn-2 种，相加正好为斐波那契数列。

 

三、 Catalan数

卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。

卡塔兰数的一般项公式为 C_n = \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{(n+1)!n!}                      另类递归式：  h(n)=((4*n-2)/(n+1))*h(n-1);

前几项为 （OEIS中的数列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

[编辑]性质

Cn的另一个表达形式为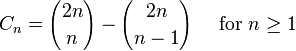C_n = {2n\choose n} - {2n\choose n-1} \quad\mbox{ for }n\ge 1 所以，Cn是一个自然数；这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)

卡塔兰数满足以下递推关系

C_0 = 1 \quad \mbox{and} \quad C_{n+1}=\sum_{i=0}^{n}C_i\,C_{n-i}\quad\mbox{for }n\ge 0.

它也满足

C_0 = 1 \quad \mbox{and} \quad C_{n+1}=\frac{2(2n+1)}{n+2}C_n,

这提供了一个更快速的方法来计算卡塔兰数。

卡塔兰数的渐近增长为

C_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}

它的含义是左式除以右式的商趋向于1当n → ∞。（这可以用n!的斯特灵公式来证明。）

所有的奇卡塔兰数Cn都满足n = 2k − 1。所有其他的卡塔兰数都是偶数。

[编辑]应用

组合数学中有非常多.的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用Cn=3和Cn=4举若干例：

  • Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
  • 将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数:
((())) ()(()) ()()() (())() (()())
  • Cn表示有n+1个叶子的二叉树的个数。

                                                                       

  • Cn表示所有不同构的含n个分枝结点的满二叉树的个数。（一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树。）

证明：

令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有{2n \choose n}个，下面考虑不满足要求的数目.

考虑一个含n个1、n个0的2n位二进制数，扫描到第2m+1位上时有m+1个0和m个1（容易证明一定存在这样的情况），则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0，则对应一个n+1个0和n-1个1的二进制数。反之亦然（相似的思路证明两者一一对应）。

从而C_n = {2n \choose n} - {2n \choose n + 1} = \frac{1}{n+1}{2n \choose n}。证毕。

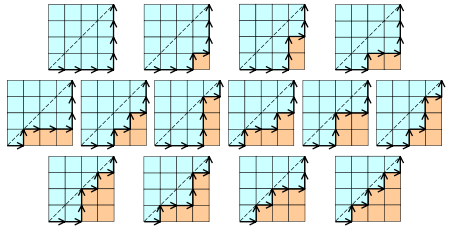
  • Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数： X代表“向右”，Y代表“向上”。下图为n = 4的情况：
  •                                                                         
  • Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n = 4的情况：

                                                                                 

  • Cn表示对{1, ..., n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ..., n), 其中S(w)递归定义如下：令w = unv，其中n为w的最大元素，u和v为更短的数列；再令S(w) =S(u)S(v)n，其中S为所有含一个元素的数列的单位元。
  • Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为 n = 4的情况:

                                                                                          



百度百科资料:
简介

　　中文:卡特兰数
　　Catalan数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
　　原理：
　　令h(0)=1,h(1)＝1,catalan数满足递归式：
　　h(n)= h(0)*h(n-1) + h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
　　该递推关系的解为：
　　h(n)=C(2n,n)/(n + 1) (n=1,2,3,)
       另类递归式：  h(n)=((4*n-2)/(n+1))*h(n-1);
　　
　　前几项为 （OEIS中的数列A000108）: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 
应用

　　我总结了一下，最典型的四类应用：（实质上却都一样，无非是递归等式的应用，就看你能不能分解问题写出递归式了）
1.括号化问题。

　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)
2.出栈次序问题。

　　一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
　　类似：
　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。

　　将一个凸多边形区域分成三角形区域的方法数?
　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
　　从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
4.给顶节点组成二叉树的问题。

　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树!
　　先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +  + h(n-1)h(0)=h(n))
　　（能构成h（N）个）

 

1. 通项公式 　

　令h(1)＝1,h(0)=1，catalan数满足递归式：

　　h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (其中n>=2)

　　另类递归式：

　　h(n)=((4*n-2)/(n+1))*h(n-1);

　　该递推关系的解为：

　　h(n)=C(2n,n)/(n+1) (n=1,2,3,...) 其中， C0=1，前几项为： 2,5,14,42,132,429,1430 。

2. 递归公式： h(n)= h(0)*h(n-1) + h(1)*h(n-2) + ... + h(n-1)h(0) (其中 n>=2)  

3. 括号问题：n 对括号可以构造出多少平衡的括号表达式？平衡的表达式就是说括号互相配对，例如 n=3 有 ((())) ， ()(()) ， (())() ， (()()) ， ()()() 五种，假设其中一个括号为 s ，那么与他配对的括号为 t ，则 s 和 t 将表达式分成三个平衡的部分，也就是括号内部，括号左边，括号右边，以右括号为分界线，那么则可以说分成两个平衡部分，括号内部和括号左边合并为一个部分。所以假设右边有 k 个括号，左边有 n-k-1 个括号（因为我们正在用一个括号 s 和 t ），所以有 Cn 通项公式的前半部分。可以将此问题拓展为连乘或连加的加括号种类问题。

4. 出栈次序问题，问1--n 入栈，有多少种出栈情况。很显然第一次可以一次性出栈 1 、 1.2 、 .... 、 1.2..k ，有 h(k) 种情况，之后剩下的就是 h(n-k) 种情况，枚举 k 后可以得到 Catalan 数的递归式。该问题可以推广如下问题：圆上 2n 个点成对连起来，求 n 条线段不想交情况；商店卖 5 元物品， n 个顾客手中有 5 元钞票， n 个顾客有十元钞票，售货员没有任何零钱。问有多少种方法使得只要十元钞票的顾客来买东西，售货员就有五元钱可以找。（可以看做持 5 元的顾客买东西为 5 元入栈，持 10 元顾客买东西为 5 元出栈）；一位大城市的市民在他所住地方的东北方（往东 n 个街区，往北 n 个街区）上班，如果他不穿越对角线，有几种走法（同样可以构造往东走为入栈，往北走为出栈）

5. 多边形三角剖分（经典的dp 题！只不过这里只要求剖分情况）一条线可以将多边形剖为两个多边形，之后递归求出两个多边形的剖分情况，最后固定一个点，枚举另一个点确定这一条线的情况数即可。

6. 给出顶点个数问能构造多少二叉树。同样枚举左边和右边子树的顶点个数，之后递归求出左右子树构造二叉树的情况。

 

四、 欧拉数（ps ：有很多欧拉数啊，不要搞混了…） F(n,k) 表示 1.2...n 的排列中恰好包含 k 次下降或者包含 k+1 次上升（例如 {3,6,1,4,5,2} 中有两个下降 {6,1}{5,2} ，三个上升 {3,6}{1,4,5},{2} ， ps ：单个数字算上升啊…）的排列个数，那么假设前 n-1 的排列中有 k 次下降，那么现在 n 插入的位置就要插到上升序列的后面（因为 n 最大，上升序列后面必为下降序列，而 n 与后面的下降数列结合还是下降数列，所以不会造成下降数列变多）因此有 k 种方法，另外假设前 n-1 的排列有 k-1 个下降，所以要放在上升序列的中间或者整个序列的开头才能保证多一个下降序列，因此有 (n-k) 种方法，递推公式为 F(n,k)=(k+1)F(n-1,k)+(n-k)F(n-1,k-1) 。

 

五、 第一类Stirling 数

设|S(n,k)| 为包含 n 个元素的集合分做 k 个环的方法数目，而 S(n,k)=S(n-1,k-1)+(n-1)S(n-1,k) 。

 

六、 第二类Stirling 数

1. 设S(n,k) 表示把 n 个元素划分成 k 个非空集合的方案数，那么假设已经分好了 n-1 个数，之后第 k 个数要么自己独立分成一个集合，要么和其他的集合合并成一个新的集合，因此有 S(n,k)=S(n-1,k-1)+k*S(n-1,k) 。其中 S(n,2)=2^(n-1)-1 ，因为设 {1}{2..n} ，那么 {2..n} 的子集有 2^(n-1) 种，也就是说 1 可以和这个子集合并形成新的集合划分，那么那个减一是如果 {2..n} 全部选上与 {1} 合并，那么就只剩下一个集合了，与题意不符。这类数的变种例如将 n 个不同的球放入 k 个相同的盒子里，且盒子不允许为空。

 

七、整数拆分，就是说整数可以分若干数之和的种类数。设F(n,k) 为将 n 拆分最大数不大于 k 的拆分法，所以要么最大数等于 k ，有 F(n-k,k) 种情况（取走一个 k ，剩下 n-k ），要么最大数小于 k ，有 F(n,k-1) 种情况。边界条件为 F(n,1)=1 ， F(0,0)=1 ， F(1,1)=1 ， F(n,k)=F(n,n)(k>n)

posted @ 2011-08-27 17:00  qingyezhu  阅读(1814)  评论(4)  编辑  收藏  举报