图

1.学习总结(2分)

1.1图的思维导图

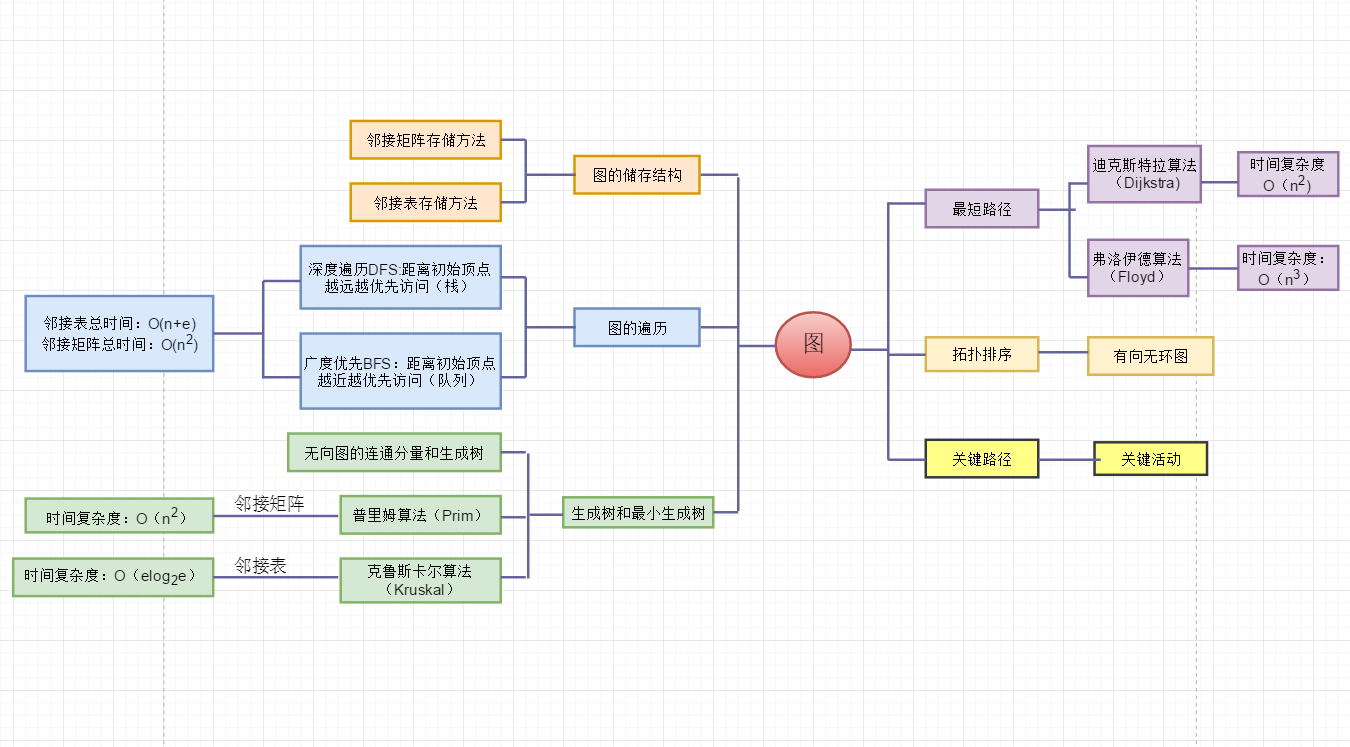
1.2 图结构学习体会

（1）深度遍历算法：距离初始顶点越远越优先访问

　　深度优先遍历过程：

　　　1）从图中某个初始顶点v出发，首先访问初始顶点v。
　　（2）选择一个与顶点v相邻且没被访问过的顶点w，再从w出发进行深度优先搜索，直到图中与当前顶点v邻接的所有顶点都被访问过为止。

　　算法设计思路：

　　（1）深度优先遍历的过程体现出后进先出的特点：用栈或递归方式实现。

　　（2）设置一个visited[] 全局数组， visited[i]=0表示顶点i没有访问； visited[i]=1表示顶点i已经访问过。

（2）广度遍历算法：距离初始顶点越近越优先访问

　　广度优先遍历的过程：

　　（1）访问初始点v，接着访问v的所有未被访问过的邻接点v1，v2，…，vt。
　　（2）按照v1，v2，…，vt的次序，访问每一个顶点的所有未被访问过的邻接点。　　　
　　（3）依次类推，直到图中所有和初始点v有路径相通的顶点都被访问过为止。

　　算法设计思路：

　　（1）广度优先搜索遍历体现先进先出的特点，用队列实现

　　（2）设置一个visited[] 数组， visited[i]=0表示顶点i没有访问； visited[i]=1表示顶点i已经访问过。

（3）Prim和Kruscal算法

　　Prim算法

　　（1）初始化U={v}。v到其他顶点的所有边为候选边；
       （2）重复以下步骤n-1次，使得其他n-1个顶点被加入到U中：
           从候选边中挑选权值最小的边输出，设该边在V-U中的顶点是k，将k加入U中；
           考察当前V-U中的所有顶点j，修改候选边：若(j，k)的权值小于原来和顶点k关联的候选边，则用(k，j)取代后者作为候选边。

　　Kruscal算法

　　（1）置U的初值等于V（即包含有G中的全部顶点），TE的初值为空集（即图T中每一个顶点都构成一个连通分量）。
      （2）将图G中的边按权值从小到大的顺序依次选取：
             若选取的边未使生成树T形成回路，则加入TE；
             否则舍弃，直到TE中包含(n-1)条边为止。

（4）Dijkstra算法

　　算法特点：

　　（1）不适用于求最长路径

　　（2）不适用于带负权值的带权图求单源最短路径

　　求解思路：

　　第1组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径v，… ，u，就将u加入到集合S中，直到全部顶点都加入到S中，算法就结束了）。
　　第2组为其余未求出最短路径的顶点集合（用U表示）。

（5）拓扑排序算法

　　（1）从有向图中选择一个没有前驱（即入度为0）的顶点并且输出它。
       （2）从图中删去该顶点，并且删去从该顶点发出的全部有向边。
       （3）重复上述两步，直到剩余的图中不再存在没有前驱的顶点为止。

2.PTA实验作业（4分）

---

2.1 题目1：图着色问题

2.2 设计思路

 while(n--)

{　

　　输入无向图的顶点数、边数、以及颜色数

　　一条边的两个端点的编号

　　待检查的颜色分配方案的个数

　　V个顶点的颜色（第i个数字表示第i个顶点的颜色）

　　是图着色问题的一个解则输出Yes，

　　否则输出No

}

2.3 代码截图

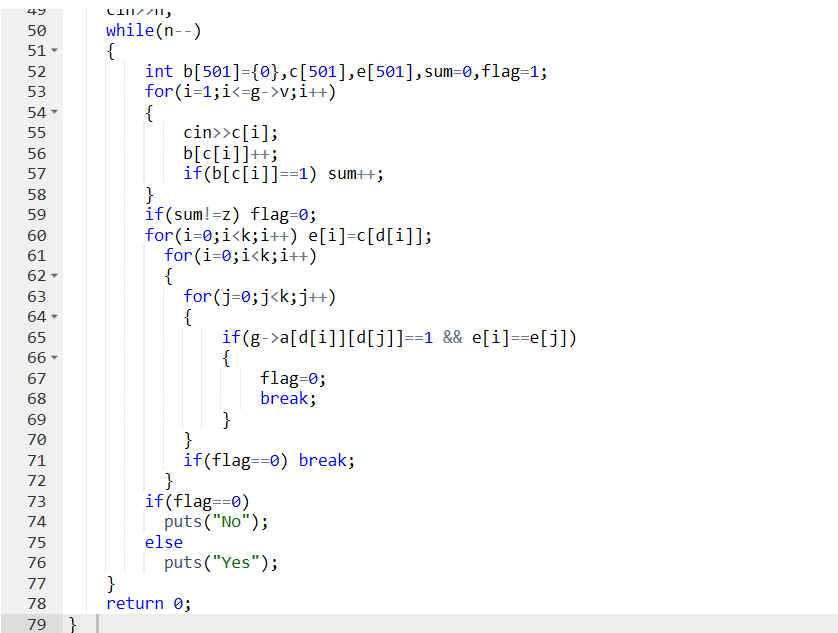
2.4 PTA提交列表说明。

 

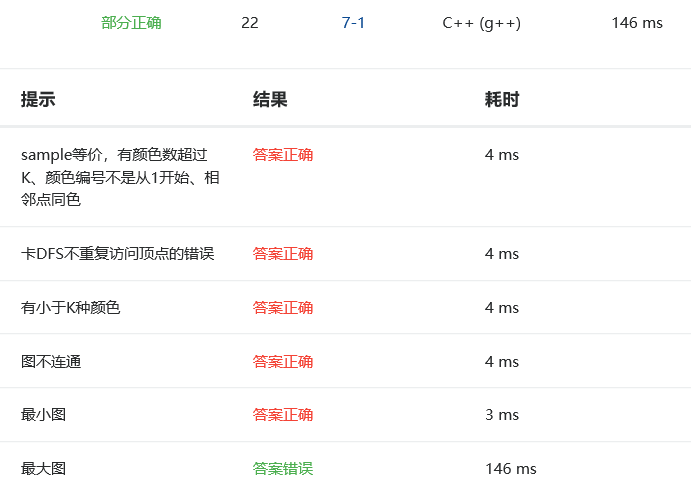
　　最大图的测试点没有过主要是一开始无向图的顶点数、边数、以及颜色数的定义不对，因为题目中说了无向图顶点数V大于0小于等于500

所以在数组定义中也认为是500，数组下标是从0开始的，把数组定义中最大界改为501就行，并且规定初始点。

题目2：排座位

2.2 设计思路

 for

{

　　如果两位宾客之间是朋友，且没有敌对关系

　　输出No problem

　　如果他们之间并不是朋友，但也不敌对

　　输出OK

　　如果他们之间有敌对，然而也有共同的朋友

　　输出OK but...

　　如果他们之间只有敌对关系

　　输出No way

}

2.3 代码截图

 

2.4 PTA提交列表说明

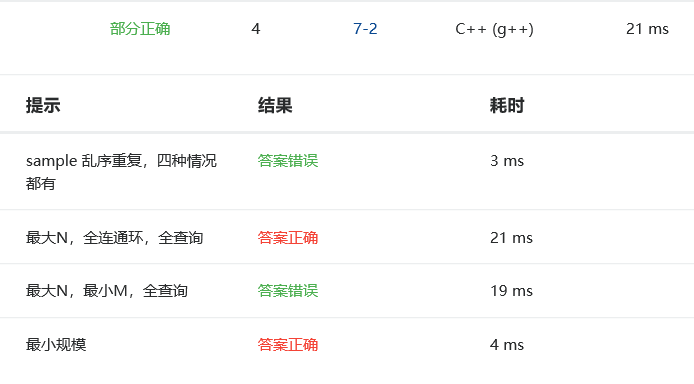
 这题有两个测试点没过，一个是乱序重复的四种情况，也就是朋友和敌对关系这两个关系的四种乱序重复另一种是最大N,最小M,全查询的情况。

如果他们之间有敌对，然而也有共同的朋友，输出OK but...；如果他们之间只有敌对关系，输出No way这两个情况时没有写上maps[x][y]==-1，

尤其是后一种情况，加上就没问题了。

题目3：公路村村通

2.2 设计思路

　　城镇数目正整数N和候选道路数目M

　　M行对应M条道路

　　该条道路直接连通的两个城镇的编号以及该道路改建的预算成本

　　如果输入数据不足以保证畅通，则输出−1

2.3 代码截图

 

 

2.4 PTA提交列表说明。

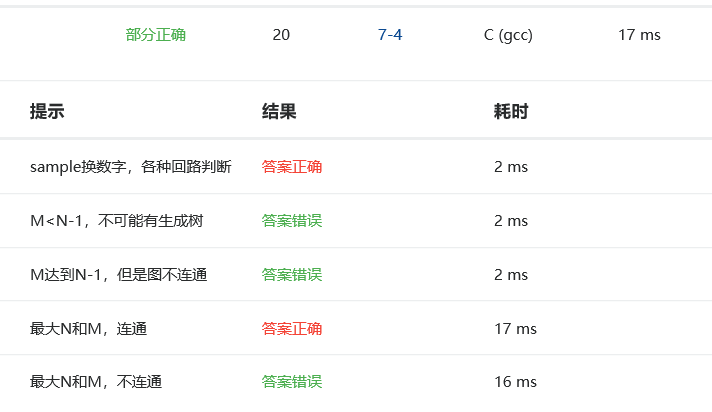
 五个测试点有三个测试点没过，M<N-1,不可能有生成树；M到达N-1，但是图不连通；最大N和M，不连通；这三种情况。

其实最重要的还是在g[i][j]=g[j][i]=999999;之前写的是99999，其实不是很懂为什么会是这里出问题了，修改之后，三个测

试点就都能通过了。

3.截图本周题目集的PTA最后排名（3分）

3.1 PTA排名（截图带自己名字的排名）

 

3.2 我的总分：110

4. 阅读代码

采用邻接矩阵或邻接表作为存储结构，完成有向图和无向图的DFS和BFS操作

#include<string.h>
#include<ctype.h>
#include<malloc.h> 
#include<limits.h>
#include<stdio.h> 
#include<stdlib.h> 
#include<io.h> 
#include<math.h> 
#include<process.h> 

//函数结果状态代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1

//#define OVERFLOW -2 因为在math.h 中已定义OVERFLOW 的值为3,故去掉此行
typedef int Status; //Status 是函数的类型,其值是函数结果状态代码，如OK 等
typedef int Boolean;// Boolean 是布尔类型,其值是TRUE 或FALSE 


#define MAX_VERTEX_NUM 20
typedef enumGraphKind; 
typedef struct ArcNode
{
	int adjvex; /* 该弧所指向的顶点的位置*/
	struct ArcNode *nextarc; /* 指向下一条弧的指针*/
	InfoType *info; /* 网的权值指针） */
}ArcNode; /* 表结点*/

typedef struct
{
	VertexType data; /* 顶点信息*/
	ArcNode *firstarc; /* 第一个表结点的地址,指向第一条依附该顶点的弧的指针*/
}VNode,AdjList[MAX_VERTEX_NUM]; /* 头结点*/
	
	typedef struct
	{
	AdjList vertices;
	int vexnum,arcnum; /* 图的当前顶点数和弧数*/
	int kind; /* 图的种类标志*/
}ALGraph;

/*ALGraphAlgo.cpp 图的邻接表存储(存储结构由ALGraphDef.h 定义)的基本操作*/
int LocateVex(ALGraph G,VertexType u)
{ 	/* 初始条件: 图G 存在,u 和G 中顶点有相同特征*/
	/* 操作结果: 若G 中存在顶点u,则返回该顶点在图中位置;否则返回-1 */
	int i;
	for(i=0;i<G.vexnum;++i)
	if(strcmp(u,G.vertices[i].data)==0)
	return i;
	return -1;
}

Status CreateGraph(ALGraph &G)
{ 	/* 采用邻接表存储结构,构造没有相关信息的图G(用一个函数构造4 种图) */
	int i,j,k;
	int w; /* 权值*/
	VertexType va,vb;
	ArcNode *p;
	printf("请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): ");
	scanf("%d",&(G.kind));
	printf("请输入图的顶点数,边数: ");
	scanf("%d,%d",&(G.vexnum),&(G.arcnum));
	printf("请输入%d 个顶点的值(<%d 个字符):\n",G.vexnum,MAX_NAME);
	for(i=0;i<G.vexnum;++i) /* 构造顶点向量*/
	{
		scanf("%s",G.vertices[i].data);
		G.vertices[i].firstarc=NULL;
	}
	if(G.kind==1||G.kind==3) /* 网*/
		printf("请顺序输入每条弧(边)的权值、弧尾和弧头(以空格作为间隔):\n");
	else /* 图*/
		printf("请顺序输入每条弧(边)的弧尾和弧头(以空格作为间隔):\n");
	for(k=0;k<G.arcnum;++k) /* 构造表结点链表*/
	{
		if(G.kind==1||G.kind==3) /* 网*/
			scanf("%d%s%s",&w,va,vb);
		else /* 图*/
			scanf("%s%s",va,vb);
		i=LocateVex(G,va); /* 弧尾*/
		j=LocateVex(G,vb); /* 弧头*/
		p=(ArcNode*)malloc(sizeof(ArcNode));
		p->adjvex=j;
		if(G.kind==1||G.kind==3) /* 网*/
		{
			p->info=(int *)malloc(sizeof(int));
			*(p->info)=w;
		}
		else
			p->info=NULL; /* 图*/
			p->nextarc=G.vertices[i].firstarc; /* 插在表头*/
			G.vertices[i].firstarc=p;
		if(G.kind>=2) /* 无向图或网,产生第二个表结点*/
		{
			p=(ArcNode*)malloc(sizeof(ArcNode));
			p->adjvex=i;
			if(G.kind==3) /* 无向网*/
			{
				p->info=(int*)malloc(sizeof(int));
				*(p->info)=w;
			}
		else
			p->info=NULL; /* 无向图*/
			p->nextarc=G.vertices[j].firstarc; /* 插在表头*/
			G.vertices[j].firstarc=p;
		}
	}
	return OK;
}

void DestroyGraph(ALGraph &G)
{ 	/* 初始条件: 图G 存在。操作结果: 销毁图G */
	int i;
	ArcNode *p,*q;
	G.vexnum=0;
	G.arcnum=0;
	for(i=0;i<G.vexnum;++i)
	{
		p=G.vertices[i].firstarc;
		while(p)
		{
			q=p->nextarc;
			if(G.kind%2) /* 网*/
				free(p->info);
			free(p);
			p=q;
		}
	}
}

VertexType* GetVex(ALGraph G,int v)
{ 	/* 初始条件: 图G 存在,v 是G 中某个顶点的序号。操作结果: 返回v 的值*/
	if(v>=G.vexnum||v<0)
		exit(ERROR);
	return &G.vertices[v].data;
}

int FirstAdjVex(ALGraph G,VertexType v)
{ 	/* 初始条件: 图G 存在,v 是G 中某个顶点*/
	/* 操作结果: 返回v 的第一个邻接顶点的序号。若顶点在G 中没有邻接顶点,则返回-1 */
	ArcNode *p;
	int v1;
	v1=LocateVex(G,v); /* v1 为顶点v 在图G 中的序号*/
	p=G.vertices[v1].firstarc;
	if(p)
		return p->adjvex;
	else
		return -1;
}

int NextAdjVex(ALGraph G,VertexType v,VertexType w)
{ 	/* 初始条件: 图G 存在,v 是G 中某个顶点,w 是v 的邻接顶点*/
	/* 操作结果: 返回v 的(相对于w 的)下一个邻接顶点的序号。*/
	/* 若w 是v 的最后一个邻接点,则返回-1 */
	ArcNode *p;
	int v1,w1;
	v1=LocateVex(G,v); /* v1 为顶点v 在图G 中的序号*/
	w1=LocateVex(G,w); /* w1 为顶点w 在图G 中的序号*/
	p=G.vertices[v1].firstarc;
	while(p&&p->adjvex!=w1) /* 指针p 不空且所指表结点不是w */
		p=p->nextarc;
	if(!p||!p->nextarc) /* 没找到w 或w 是最后一个邻接点*/
		return -1;
	else /* p->adjvex==w */
		return p->nextarc->adjvex; /* 返回v 的(相对于w 的)下一个邻接顶点的序号*/
}

Boolean visited[MAX_VERTEX_NUM]; /* 访问标志数组(全局量) */
void(*VisitFunc)(char* v); /* 函数变量(全局量) */
void DFS(ALGraph G,int v)
{ /* 从第v 个顶点出发递归地深度优先遍历图G。算法7.5 */
	int w;
	VertexType v1,w1;
	strcpy(v1,*GetVex(G,v));
	visited[v]=TRUE; /* 设置访问标志为TRUE(已访问) */
	VisitFunc(G.vertices[v].data); /* 访问第v 个顶点*/
	for(w=FirstAdjVex(G,v1);w>=0;w=NextAdjVex(G,v1,strcpy(w1,*GetVex(G,w))))
		if(!visited[w])
			DFS(G,w); /* 对v 的尚未访问的邻接点w 递归调用DFS */
}
void DFSTraverse(ALGraph G,void(*Visit)(char*))
{ /* 对图G 作深度优先遍历。算法7.4 */
	int v;
	VisitFunc=Visit; /* 使用全局变量VisitFunc,使DFS 不必设函数指针参数*/
	for(v=0;v<G.vexnum;v++)
		visited[v]=FALSE; /* 访问标志数组初始化*/
	for(v=0;v<G.vexnum;v++)
		if(!visited[v])
			DFS(G,v); /* 对尚未访问的顶点调用DFS */
	printf("\n");
}

typedef int QElemType; /* 队列类型*/
#include"LinkQueueDef.h"
#include"LinkQueueAlgo.h"
void BFSTraverse(ALGraph G,void(*Visit)(char*))
{	/*按广度优先非递归遍历图G。使用辅助队列Q 和访问标志数组visited。算法7.6 */
	int v,u,w;
	VertexType u1,w1;
	LinkQueue Q;
	for(v=0;v<G.vexnum;++v)
		visited[v]=FALSE; /* 置初值*/
	InitQueue(Q); /* 置空的辅助队列Q */
	for(v=0;v<G.vexnum;v++) /* 如果是连通图,只v=0 就遍历全图*/
		if(!visited[v]) /* v 尚未访问*/
		{
			visited[v]=TRUE;
			Visit(G.vertices[v].data);
			EnQueue(Q,v); /* v 入队列*/
			while(!QueueEmpty(Q)) /* 队列不空*/
			{
				DeQueue(Q,u); /* 队头元素出队并置为u */
				strcpy(u1,*GetVex(G,u));
				for(w=FirstAdjVex(G,u1);w>=0;w=NextAdjVex(G,u1,strcpy(w1,*GetVex(G,w))))
				if(!visited[w]) /* w 为u 的尚未访问的邻接顶点*/
				{
					visited[w]=TRUE;
					Visit(G.vertices[w].data);
					EnQueue(Q,w); /* w 入队*/
				}
			}
		}
	printf("\n");
}

void Display(ALGraph G)
{	 /* 输出图的邻接矩阵G */
	int i;
	ArcNode *p;
	switch(G.kind)
	{ 	case DG: printf("有向图\n"); break;
		case DN: printf("有向网\n"); break;
		case AG: printf("无向图\n"); break;
		case AN: printf("无向网\n");
	}
	printf("%d 个顶点：\n",G.vexnum);
	for(i=0;i<G.vexnum;++i)
		printf("%s ",G.vertices[i].data);
	printf("\n%d 条弧(边):\n",G.arcnum);
	for(i=0;i<G.vexnum;i++)
	{
		p=G.vertices[i].firstarc;
		while(p)
		{
				if(G.kind<=1) /* 有向*/
				{
					printf("%s→%s ",G.vertices[i].data,G.vertices[p->adjvex].data);
					if(G.kind==DN) /* 网*/
						printf(":%d ",*(p->info));
				}
			else /* 无向(避免输出两次) */
			{
				if(i<p->adjvex)
				{
					printf("%s－%s ",G.vertices[i].data,G.vertices[p->adjvex].data);
					if(G.kind==AN) /* 网*/
						printf(":%d ",*(p->info));
				}
			}
			p=p->nextarc;
		}
		printf("\n");
	}
}
	
	
#include "pubuse.h"
#define MAX_NAME 3 /* 顶点字符串的最大长度+1 */
typedef int InfoType; /* 存放网的权值*/
typedef char VertexType[MAX_NAME]; /* 字符串类型*/
#include"ALGraphDef.h"
#include"ALGraphAlgo.h"
void print(char *i)
{
    printf("%s ",i);
}

void main()
{
	int i,j,k,n;
	ALGraph g;
	VertexType v1,v2;
	printf("请选择有向图\n");
	CreateGraph(g);
	Display(g);
	printf("深度优先搜索的结果:\n");
	DFSTraverse(g,print);
	printf("广度优先搜索的结果:\n");
	BFSTraverse(g,print);
	DestroyGraph(g); /* 销毁图*/
}