不等式选讲习题
(1)\((a+b)(a^5+b^5)\ge 4\)
分析:证明过程当中你必然得想着,要设法用上已知的条件\(a>0,b>0,a^3+b^3=2\),
所以可以这样
\((a+b)(a^5+b^5)=a^6+b^6+ab^5+a^5b=(a^3+b^3)^2-2a^3b^3+ab^5+a^5b\)
\(=4+ab(a^4-2a^2b^2+b^4)=4+ab(a^2-b^2)^2\ge 4\)
当且仅当\(a=b\)时取到等号。命题得证。
(2)\(a+b\leq 2\)
分析:\(a+b\leq 2\Longleftrightarrow (a+b)^3\leq 2^3\),这样思考是为了用上已知条件。
\((a+b)^3=a^3+3a^2b+3ab^2+b^3=2+3ab(a+b)\leq 2+3\times (\cfrac{a+b}{2})^2\times(a+b)\)
\(=2+3\times\cfrac{(a+b)^3}{4}\)
故,转化为\(\cfrac{1}{4}(a+b)^3\leq 2\),即\((a+b)^3\leq 8\),故\(a+b\leq 2\)。命题得证。
(1)当\(a=1\)时,求不等式\(f(x)\ge g(x)\)的解集。
法1:零点分区间讨论法,我们先转化函数\(g(x)\)为分段函数,分别令\(x+1=0\)和\(x-1=0\),得到\(x=-1\)和\(x=1\),这样这两个实数就把数轴分成了三段,分三类情况讨论如下
\(g(x)=\begin{cases}-x-1-x+1,&x\leq -1\\x+1-x+1,&-1<x<1\\x+1+x-1,&x\ge 1\end{cases}\),整理得到\(g(x)=\begin{cases}-2x,&x\leq -1\\2,&-1<x<1\\2x,&x\ge 1\end{cases}\),
当\(a=1\)时,\(f(x)=-x^2+x+4\),则\(f(x)\ge g(x)\)就等价转化为以下三个不等式组:
\(\begin{cases}x\leq -1\\-x^2+x+4\ge -2x\end{cases}\)或者\(\begin{cases}-1< x< 1\\-x^2+x+4\ge 2\end{cases}\)或者\(\begin{cases}x\ge 1\\-x^2+x+4\ge 2x\end{cases}\)
分别解得\(x\leq -1\)或\(-1<x<1\)或\(1\leq x\leq \cfrac{\sqrt{17}-1}{2}\),求其并集得到原不等式的解集为\([-1,\cfrac{\sqrt{17}-1}{2}]\)。

法2:分别作出两个函数的图像,再求得交点,有图像可以直观的看到原不等式的解集为\([-1,\cfrac{\sqrt{17}-1}{2}]\)。
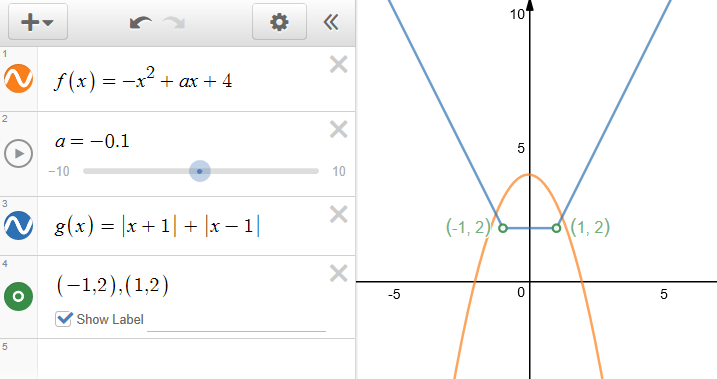
(2)若不等式\(f(x)\ge g(x)\)的解集包含\([-1,1]\),求\(a\)的取值范围。
法1:数形结合法,函数\(f(x)=-x^2+ax+4\),对称轴为\(x=\cfrac{a}{2}\),开口向下,由有图可知,要使得不等式\(f(x)\ge g(x)\)的解集包含\([-1,1]\),只需要满足条件\(\begin{cases}f(-1)\ge 2\\f(1)\ge 2\end{cases}\),解得\(\begin{cases}a\leq 1\\a\ge -1\end{cases}\),故\(a\)的取值范围为\([-1,1]\)。
法2:转化为不等式恒成立求解,当\(x\in [-1,1]\)时,\(g(x)=2\),由题目可知,不等式\(f(x)\ge 2\)的解集包含\([-1,1]\),即当\(x\in [-1,1]\)时,\(f(x)\ge 2\)恒成立,即\(-x^2+ax+2\ge 0\)恒成立,
令\(h(x)=-x^2+ax+2\),则只需满足条件\(\begin{cases}h(-1)\ge 0\\h(x)\ge 0\end{cases}\),解得\(-1\leq a \leq 1\),故\(a\)的取值范围为\([-1,1]\)。
法3:恒成立+分离参数法
当转化得到\(x\in [-1,1]\)时,\(f(x)\ge 2\)恒成立,即\(-x^2+ax+2\ge 0\)恒成立,接下来准备分离参数:
\(1^。\)当\(x=0\)时,代入得到\(2\ge 0\),即\(a\in R\);
\(2^。\)当\(x<0\)时,由\(ax\ge x^2-2\)分离参数得到\(a\leq \cfrac{x^2-2}{x}=x-\cfrac{2}{x}\),令\(h(x)=x-\cfrac{2}{x}\),\(h(x)\)在区间\((-1,0)\)上单调递增,故\(h(x)_{min}\rightarrow h(-1)=1\)即\(a\leq 1\);
\(3^。\)当\(x>0\)时,由\(ax\ge x^2-2\)分离参数得到\(a\ge \cfrac{x^2-2}{x}=x-\cfrac{2}{x}\),令\(h(x)=x-\cfrac{2}{x}\),\(h(x)\)在区间\((0,1)\)上单调递增,故\(h(x)_{max}\rightarrow h(1)=-1\)即\(a\ge -1\);
综上所述,由于三种情形下都要成立,故需要取其交集得到\(a\)的取值范围为\([-1,1]\)。
法1:分段函数法,由上可知,\(g(x)=\begin{cases}-2x,&x\leq -1\\2,&-1<x<1\\2x,&x\ge 1\end{cases}\),
在每一段上求其最小值,就得到整个定义域上的函数\(g(x)_{min}=2\);
法2:图像法,作出函数\(g(x)\)的图像,由图像可知,\(g(x)_{min}=2\);
法3:绝对值不等式法,\(g(x)=|x+1|+|x-1|\ge |(x+1)-(x-1)|=2\),
当且仅当\(-1\leq x\leq 1\)时取等号。故\(g(x)_{min}=2\);
法4:绝对值的几何意义法,如图所示

由数轴图可知,当实数\(x\)所对应的点\(C\)位于点\(A\)(对应实数\(-1\))和\(B\)(对应实数\(1\))之间时 ,\(|x+1|+|x-1|=|AC|+|BC|=|AB|=2\);
当实数\(x\)所对应的点\(C\)位于点\(A\)左侧,或者点\(B\)右侧时 ,\(|x+1|+|x-1|=|AC|+|BC|>|AB|=2\);
故我们能直观的知道函数\(g(x)=|x+1|+|x-1|\)的最小值为\(2\)。
法1:分段函数法,仿上例完成;\(h(x)_{min}=-2;h(x)_{max}=2\);
法2:图像法,\(h(x)_{min}=-2;h(x)_{max}=2\);

法3:绝对值不等式法,由于\(||x+1|-|x-1||\leq |(x+1)-(x-1)|=2\),故\(-2\leq |x+1|-|x-1|\leq 2\);故\(h(x)_{min}=-2;h(x)_{max}=2\);
(1)求不等式\(f(x)\ge 1\)的解集;
法1:分段函数法,仿照上面2017全国卷1文科理科第23题法1的解法,我们可以很容易得到分段函数\(f(x)=\begin{cases}-3,&x<-1\\2x-1,&-1\leq x\leq 2\\3&x>2\end{cases}\),这样不等式\(f(x)\ge 1\)等价于以下三个不等式组:
\(\begin{cases}x< -1\\-3\ge1\end{cases}\)或者\(\begin{cases}-1\leq x\leq 2\\2x-1\ge 1\end{cases}\)或者\(\begin{cases}x>2\\3\ge1\end{cases}\)

分别解得\(x\in\varnothing\),或\(1\leq x \leq 2\),或\(x>2\),求并集得到解集\(x\in [1,+\infty)\)。
法2:数形结合图像法,其中红色的是函数\(f(x)=|x+1|-|x-2|\)图像,蓝色的是函数\(g(x)=1\)的图像由图像可以直观看出解集为\(x\in [1,+\infty)\)。
(2)若不等式\(f(x)\ge x^2-x+m\)的解集非空,求\(m\)的取值范围;
分析:已知不等式解集非空求参数范围类题目,我们常常转化为分离参数+能成立,比如先分离参数得到\(m\leq f(x)-x^2+x=h(x)\),接下来想办法求新构造函数\(h(x)\)的最大值就可以了。
法1:【高考给定解法】\(h(x)=f(x)-x^2+x=|x+1-|x-2|-x^2+x\leq |x|+1+|x|-2-x^2+|x|=-(|x|-\frac{3}{2})^2+\cfrac{5}{4}\leq \cfrac{5}{4}\);且当\(x=\cfrac{3}{2}\)时,\(|x+1|-|x-2|-x^2+x= \cfrac{5}{4}\),故\(m\)的取值范围是\((-\infty, \cfrac{5}{4}]\)。
说明:本解法用到了放缩法,不太好掌握。
法2:将\(h(x)\)转化为分段函数求其最大值。
\(h(x)=f(x)-x^2+x=\begin{cases}-x^2+x-3,&x<-1\\-x^2+x+2x-1,&-1\leq x\leq 2\\-x^2+x+3,&x>2 \end{cases} =\begin{cases}-(x-\frac{1}{2})^2-\frac{11}{4},&x<-1\\ -(x-\frac{3}{2})^2+\frac{5}{4},&1\leq x\leq 2\\-(x-\frac{1}{2})^2+\frac{13}{4},&x>2 \end{cases}\)
故\(h(x)_{max}=\begin{cases}-3,&x<-1\\ \frac{5}{4},&1\leq x \leq 2\\1,&x>2\end{cases}\),故在整个定义域上\(h(x)_{max}=\cfrac{5}{4}\);
故要使得\(m\leq h(x)\)的解集非空,必须满足\(m\leq \cfrac{5}{4}\),即\(m\)的取值范围是\((-\infty, \cfrac{5}{4}]\)。
柯西不等式:\((a^2+b^2)(c^2+d^2)\ge (ac+bd)^2,a,b,c,d\in R\);
绝对值不等式:\(||a|-|b||\leq |a+b|\leq |a|+|b|\);
分析:\(2^c=2^a+2^b\ge 2\sqrt{2^a\cdot 2^b}\),
即\(2^c\ge 2\sqrt{2^{a+b}}\)
即\(2^{2c}\ge 2^2\cdot 2^{a+b}=2^{2+a+b}\),
则\(a+b-2c\leq -2\),当且仅当\(a=b,c=a+1\)时取到。
故\((a+b-2c)_{max}=-2\)。
反思:本题目还可以考虑两边同除以\(2^c\) ,变形为\(2^{a-c}+2^{b-c}=1\)。
则\(1\ge 2\sqrt{2^{a-c}2^{b-c}}\),即\(1\ge 2\sqrt{2^{a+b-2c}}\)
即\(1\ge 2^2\cdot 2^{a+b-2c}\),即\(2^{-2}\ge 2^{a+b-2c}\)
即\(a+b-2c\leq 2c\),其余同上法。
(1)当\(a=1\)时,求不等式\(f(x)\ge 0\)的解集。
分析:分区间讨论法,解集为\([-2,3]\),详解过程略。
(2)若\(f(x)\leq 1\),求\(a\)的取值范围。
分析:本题目没有给定解集\(D\),却需要求参数\(a\)的取值范围,那我们可以这样想,
对于未知解集\(D\)内的任意一个\(x\),必然满足\(f(x)\leq 1\),即对解集\(D\)而言,不等式\(f(x)\leq 1\)恒成立,
即\(5-|x+a|-|x-2|\leq 1\)恒成立,即\(|x+a|+|x-2|\ge 4\)恒成立,
这样难点就转换为求\((|x+a|+|x-2|)_{min}\),
又\(|x+a|+|x-2|\ge |(x+a)-(x-2)|=|a+2|\),
即\((|x+a|+|x-2|)_{min}=|a+2|\),
即\(|a+2|\ge 4\),则\(a+2\ge 4\)或\(a+2\leq -4\)
解得\(a\leq -6\)或\(a\ge 2\)。
分析:由柯西不等式可知,\((x^2+y^2+z^2)\cdot (2^2+3^2+1^2)\ge (2\cdot x+3\cdot y+1\cdot z)^2\)
当且仅当\(\cfrac{x}{2}=\cfrac{y}{3}=\cfrac{z}{1}\)时取到等号;
即\(14(x^2+y^2+z^2)\ge 49\),即\(x^2+y^2+z^2\ge \cfrac{49}{14}\);
(1)求不等式\(f(x)<8\)的解集;
提示:分区间讨论法,转化为分段函数不等式求解,解集\((-3,1)\)。
(2)若\(a>0\),\(b>0\),且方程\(f(x)=3a+2b\)有且仅有一个实数根,求\(\cfrac{9}{2a+b}+\cfrac{4}{a+b}\)的最小值;
分析:由(1)可知,\(f(x)=\left\{\begin{array}{l}{-3x-1,x\leqslant -2}\\{x+7,-2<x<3}\\{3x+1,x\geqslant 3}\end{array}\right.\)
故函数\(f(x)\)在\((-\infty,-2)\)上单调递减,在\([-2,+\infty)\)上单调递增,
由于方程\(f(x)=3a+2b\)有且仅有一个实数根,故可知\(3a+2b=f(-2)=5\),
[备注:此时\(3a+2b\)理解为一个整体,比如\(3a+2b=m\),即方程\(f(x)=m\)有且仅有一个根,即函数\(y=f(x)\)与\(y=m\)仅有一个交点。]
即\((2a+b)+(a+b)=5\),且\(a>0\),\(b>0\),求\(\cfrac{9}{2a+b}+\cfrac{4}{a+b}\)的最小值;
\(\cfrac{9}{2a+b}+\cfrac{4}{a+b}=\cfrac{1}{5}(\cfrac{9}{2a+b}+\cfrac{4}{a+b})\times 5\)\(\cfrac{1}{5}(\cfrac{9}{2a+b}+\cfrac{4}{a+b})[(2a+b)+(a+b)]\)
\(=\cfrac{1}{5}(9+4+\cfrac{9(a+b)}{2a+b}+\cfrac{4(2a+b)}{a+b})\geqslant \cfrac{13}{5}+\cfrac{1}{5}\times 2\sqrt{\frac{9(a+b)}{2a+b}\times \frac{4(2a+b)}{a+b}}\)\(=\cfrac{13}{5}+\cfrac{12}{5}=5\)
当且仅当\(\cfrac{9(a+b)}{2a+b}=\cfrac{4(2a+b)}{a+b}\),即\(a=b=1\)时取等号。
故\(\cfrac{9}{2a+b}+\cfrac{4}{a+b}\)的最小值为\(5\).
(1).解关于\(x\)的不等式\(f(x)+a-1>0(a\in R)\);
分析:不等式\(f(x)+a-1>0\),即\(|x-2|+a-1>0\),即\(|x-2|>1-a\),
当\(a=1\)时,解集为\(x\neq 2\),即\((-\infty,2)\cup(2,+\infty)\);
当\(a>1\)时,解集为全体实数\(R\);
当\(a<1\)时,由\(|x-2|>1-a\)可得,\(x-2>1-a\)或\(x-2<a-1\),则得到\(x>3-a\)或\(x<a+1\),
故解集为\((-\infty,a+1)\cup(3-a,+\infty)\).
(2).若函数\(f(x)\)的图象恒在函数\(g(x)\)图象的上方,求\(m\)的取值范围.
分析:\(f(x)\)的图象恒在函数\(g(x)\)图象的上方,即为\(|x-2|>-|x+3|+m\)对任意实数\(x\)恒成立,即\(|x-2|+|x+3|>m\)恒成立.
又对任意实数\(x\)恒有\(|x-2|+|x+3|\geqslant |(x-2)-(x+3)|=5\),于是得\(m<5\),
即\(m\)的取值范围是\((-\infty,5)\).
(1).当\(a=1\)时,求不等式\(f(x)\geqslant 5\)的解集;
分析:用分区间讨论法,求解得到解集为\(\{x\mid x\leqslant -3或x\geqslant 2\}\).
(2).若\(f(x)\leqslant 3-x\)的解集为\(A\)且\([-4,-2]\)是集合\(A\)的子集,求\(a\)的取值范围。
分析:由题意可知,\(f(x)\leqslant 3-x\)在区间\([-4,-2]\)上恒成立,
即\(|ax-1|-x-2\leqslant 3-x\)在区间\([-4,-2]\)上恒成立,即\(|ax-1|\leqslant 5\)在区间\([-4,-2]\)上恒成立,
即\(-4\leqslant ax\leqslant 6\)在区间\([-4,-2]\)上恒成立,由于\(x\in [-4,-2]\)
则\(\left\{\begin{array}{l}{-4\leqslant -4a\leqslant 6}\\{-4\leqslant -2a\leqslant 6}\end{array}\right.\quad\) 即\(\left\{\begin{array}{l}{-\cfrac{3}{2}\leqslant a\leqslant 1}\\{-3\leqslant a\leqslant 2}\end{array}\right.\),解得即\(-\cfrac{3}{2}\leqslant a\leqslant 1\)
故\(a\)的取值范围是\([-\cfrac{3}{2},1]\).




 不等式选讲习题
不等式选讲习题

