统计01：概述

作者：Vamei 出处：http://www.cnblogs.com/vamei 严禁转载。 

 

完成了概率论之后，数据之旅的下一站就是统计。统计是研究数据的学科。它包括了数据很多方面，比如如何描述数据、如何通过抽样推测整体的信息、如何通过数据判断假设的真伪。近年来，“数据科学”成为一门显学。统计随之风生水起，成为人们竞相谈论的话题。文艺作品自然不会错过这个热点。在电影“点球成金”中，布拉德·皮特饰演的球队经理，就利用统计方法来搜寻球员和管理球队，最终造就了一支劲旅。

《点球成金》

 

我将在这篇文章中将对统计进行概述，以便于你在深入学习统计之前，对统计有一个基本概念。

 

统计的历史

其实在统计诞生之前，很多人已经有了数据意识。刘邦占领咸阳后，萧何先去王宫中收集的，正是户籍、地理、人口等手册。后来楚霸王项羽来了，抢夺的却是金银珠宝。可以说，在楚汉相争开始之前，刘邦已经在信息上胜了项羽。英国的“征服者”威廉也很有数据意识。威廉以旺盛的精力统治着英格兰。他派遣手下，走遍英格兰的每个村庄，编纂成《统计书》 (Domesday Book)，详细的记录了英格兰每个地区的人口、地理和物产，甚至于精确到每家养殖的牲口数目。当然，威廉收集数据的目的并不单纯。只有掌握了这些数据，他才能清楚地知道贵族的财产，然后就可以不客气的征税。

 

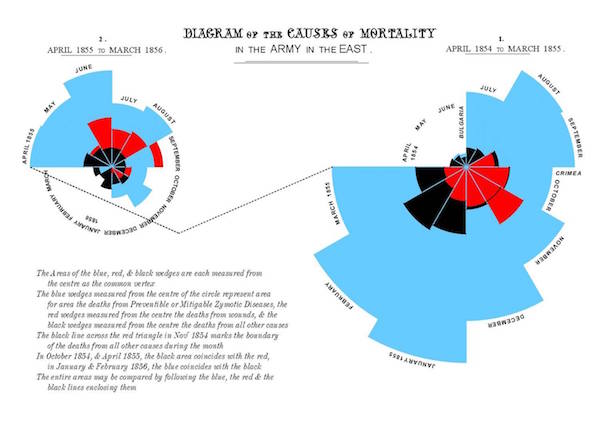
现代意义的统计学诞生于近代的欧洲，主要服务于政府部门。“统计”英文是statistics，词根就源于state，也就是“国家”。近代欧洲战火不断，耗资巨大。政府必须搜刮到足够多的税收，才能弥补国库亏空。“统计”因此成了君王不可或缺的工具。另一方面，以经验主义为基础的现代科学开始孵化。对于伽利略和培根这样的科学家来说，实验产生的数据是科学的唯一基石。统计方法作为整理和描述数据的手段，变得不可或缺。在政府行政和科学发展的双料刺激下，统计发展成一门独立的学科，其思想影响到诸多领域。南丁格尔在议会演讲时，就用统计图的方式，向议员们说明克里米亚前线糟糕的卫生状况，促使了战地医院的诞生。

南丁格尔的统计图。用以说明卫生改善后，兵营中感染数目的减少。

 

但在很长的历史时期里，统计并不被认为是数学的分支。人们只是把统计当做数据收集和数据描述的代名词。十七世纪的科学家甚至有轻视数据的倾向。这个时代的科学家普遍信奉“决定论”。他们认为，所谓的数据是由绝对精确的物理规律产生出来的，数据中的落差都是由于“不完美”的实验设计。到了十八世纪，科学理论进一步发展，用于验证理论的观测也变得越来越精细。科学家必须排除数据中的随机因素，才能验证理论的真伪。这个时代的拉普拉斯就因为找不到足够多的数据，否定了自己的潮汐理论。不过，统计的理论基础依然很粗糙。

 

到了二十世纪初，概率论完成了理论体系的建设，统计学家才看到严格化统计学的希望。统计学家把抽样理解为概率论中的“随机事件”，从而在概率论和统计之间建立了桥梁。统计因此找到了坚实的理论基础，正式成为一门数学分支。以此为起点，统计学的影响力进一步扩大。日本二战后的“产业奇迹”，就离不开统计带来的高水平生产管控。在农业育种和药物实验方面，统计也是最常用的数学工具。在生物工程、网络安全、人工智能等新兴领域，统计也都起到了关键作用。可以说，统计已经成为现代社会不可或缺的基础设施。

 

群体

统计研究的对象是某个群体(population)。群体包括了与问题相关的所有个体。我们想了解世界人口，那么群体就由世界上所有的人组成。如果我们想了解学生的身高，那么群体就包括了所有学生的身高值。收集群体中所有个体的数据，是了解一个群体最完备的方法。这个文件中就包括了一个学校所有学生的身高值。对此有兴趣的人，当然可以打开文件逐行查看。但人脑存储和处理信息的能力有限，因此往往看不了几行就会头晕脑胀。我们需要描述群体数据的办法。

 

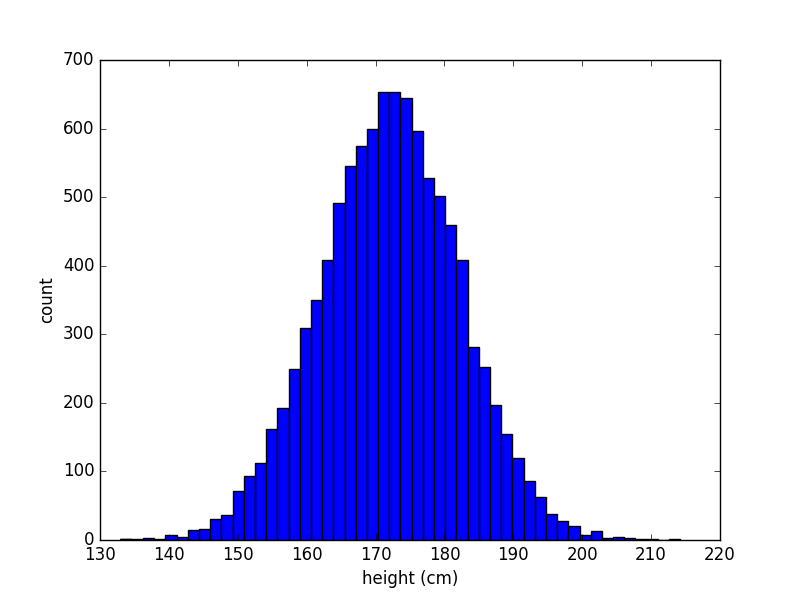
一种办法是画图。画图可以把数字信息变得几何化，从而让统计数据变得容易理解。我们用常见的条形分布图来画学生身高的分布：

 

这种条形分布图把身高在某个范围内的学生总数绘成一个竖直的长条。这个长条的宽度是身高的范围，高度是学生总数。数据绘图一定程度上简化了数据的信息量。从这种图中，你没法完整得获得原始数据。不过，这样的简化让数据变得更容易读。上面的绘图很容易编程实现，绘图程序为：

import numpy as np
import matplotlib.pyplot as plt

with open("xiangbei_height.txt", "r") as f:
    lines = f.readlines()

x = list(map(float, lines))

plt.hist(x, 50)
plt.xlabel("height (cm)")
plt.ylabel("count")
plt.show()

 

另一个办法是根据群体来计算群体参数(population parameter)，比如群体的平均值和方差。这些参数用一个单一数字来代表群体某一方面的信息。群体平均值(population mean)可以反映群体总体状况。它的定义如下：

$$\mu=\frac{1}{N} \sum_{i=1}^N x_i$$

 

群体方差(population variance)则可以反映群体的离散状况，定义如下：

$$\sigma^2=\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2$$

 

从群体平均值和群体方差就可以读出很多信息。比如下面列出两所学校的群体参数。可以看出，陵南的学生总体身高比较高，而湘北不同学生之间身高差异比较大：

	陵男中学	湘北中学
群体平均值	178	172
群体方差	16	100

 

群体参数还有很多，比如群体总和、群体中位数等等。这些参数都可以从群体数据中计算出来，并反映出群体的某个特性，从而方便人们理解群体的信息。

 

统计推断

我们来看一个典型的统计问题：工厂生产了1万个产品，要如何检查产品的合格率？

 

最直接的想法是，一个一个地检查每个产品，也就是收集整个群体的数据。统计中的数据描述就起到了类似的作用。我们可以用表格或绘图的方式来描述群体数据，比如：

不合格	合格
50	9950

 

 

如果能完整地收集到群体的数据，那么统计就变得简单了很多。但很多时候，我们难以准确地获得群体的数据。就拿世界人口来说，由于每一秒都有人出生和死亡，所以很难即时的搜集群体的信息。再拿全球气温来说，也很难在整个地球上布满温度传感器，获得所有的温度数据。而在一些情境下，就算可以收集整个群体的数据，人们也会因为效率放弃。回到工厂的例子。工厂的生产往往遵守事件安排。如果检测1万个产品需要耗费很长时间，那么就会变得不可行。这时候，工厂经理想到一个朴素的办法：抽样(sampling)。

 

工厂经理从1万个产品中拿出1000个进行检测。根据他的经验，如果这1000个都没有问题，那么整批产品很可能没有什么问题。如果这1000个中有很多都是不合格的，那么整批产品很可能出了大问题。所谓的抽查，就是从群体中抽取一个子集作为样本(sample)。用方文山的歌词来总结抽样，再贴切不过：

繁华如三千东流水，我只取一瓢饮。

 

工厂经理随后的推论，就是在用样本来推测群体的信息。这被称为统计推断(statistical inference)。然而，样品是从群体抽取的部分个体，抽样的结果受到随机性影响。就拿我们在表格中记录的群体信息为例。工厂经理可能正好没有抽到任何次品，也可能在样本中包括了所有的次品。即使群体没有发生变化，统计推断也会因为样品的随机性而发生变化。这会带来恼人的问题，比如说车间主任会质疑经理的抽样结果，认为经理的推断受到随机性影响。因此，经理有必要定量化推论的不确定性。幸运的是，统计学家已经给出了一套大家都接受的方法，车间主任也不用老是和工厂经理扯皮。

 

样本

把抽样看作一个随机事件，是统计向概率论靠拢的关键。抽样所有可能的结果，就构成了我们的样本空间。当我们从N个群体成员中抽取n个样品成员时，就有[$ \left( \begin{array}{c} N \\ n \end{array} \right) $]种可能的结果。这些结果就构成了样本空间。

 

举例来说，放在罐子里的甲、乙、丙三个球作为群体，从中抽取两个球。样本空间就包含了三个元素：

[$\{ 甲球和乙球, 甲球和丙球, 乙球和丙球 \}$]

在这个例子中，群体中包含了3个成员，样本抽取了其中的两个。

 

如果抽样时等概率事件，即三种抽样结果的概率都是1/3：

$$P(甲球和乙球) = 1/3$$

$$P(甲球和丙球) = 1/3$$

$$P(乙球和丙球) = 1/3$$

 

我们再进一步，考虑每个成员的取值。我们抽样时，感兴趣的往往是群体某个方面的特征。比如球的颜色，或者学生的身高。群体成员的取值情况，就构成了群体的分布。如果样本中包含了n个成员，我们就用[$X_1,X_2,...,X_n$]表示成员们的取值。群体中的成员各不相同，但取值却完全有可能相同。这样的话，取值的概率分布就会变得非常多样化。甲、乙、丙球分别取红、黄、蓝颜色时，第一个抽样成员[$X_1$]的分布：

$$P(X_1=红)=1/3$$

$$P(X_1=黄)=1/3$$

$$P(X_1=蓝)=1/3$$

 

如果在另一个罐子中，群体的配色发生了变化。甲、乙球取红色，丙球取蓝色，那么抽样成员[$X_1$]的分布就变成了：

$$P(X_1=红)=2/3$$

$$P(X_1=蓝)=1/3$$

也就是说，群体取值的变化，会造成样品取值概率分布的变化。三个球的系统中，群体就有下面10种可能：

红 黄 蓝
1  1  1
2  1  0
2  0  1
1  2  0
0  2  1
1  0  2
0  1  2
0  0  3
0  3  0
3  0  0

每种情况下，[$X_1, X_2$]都会有一种特定的概率分布。

 

为了研究方便，统计中经常采用理想化的抽样方法，也就是所谓的简单随机抽样（simple random sampling）。简单随机抽样中，[$X_1, X_2, ..., X_n$]相互独立，并且有相同的分布(iid random variables)。简单随机抽样产生的样品被称为随机样品（random sample）。值得注意的是，在上面抽小球的例子中，尽管[$X_1$]和[$X_2$]有相同的分布，但两者之间不独立，所以并非简单随机抽样。在实际操作上来说，抽样大部分是不重复的。当某个成员被抽中时，会影响到其他成员被抽中的概率，很难让成员取值相互独立。不过，当样品大小远远小于群体大小时，可以近似地认为是随机抽样。

 

样品统计量

建立在样品之上，还有一个简单而重要的概念，就是样品统计量(sample static)。我们知道，样品成员的取值构成了一组随机变量[$X_1, X_2, ..., X_n$]。所谓的样品统计量，就是定义在这组随机变量上的函数，即

$$sample\ static=T(X_1, X_2, ..., X_n)$$

通过之前在概率论中的学习，我们知道随机变量的函数也是随机变量。因此，样品统计量也是有一定概率分布的随机变量。当[$X_1, X_2, ..., X_n$]的分布确定时，样品统计量的分布也就确定了下来。样品平均值和样品方差都是常见的样品统计量：

$$\overline{X} = \frac{1}{n} \sum_{i=1}^n X_i$$

$$S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \overline{X})^2$$

 

应该注意到，样品统计量和群体参数之间的不同。样品统计量是一个随机变量，而群体参数却是一个具体的数字。但两者之间又有联系。对于随机样品来说，如果它来自的群体平均值为[$\mu$]、方差为[$\sigma^2$]，那么可以证明：

$$E(\overline{X})=\mu$$

$$E(S^2)=\sigma^2$$

当然，这也并非巧合。样品统计量只是定义在样品上的函数，所以可以灵活地选择形式。统计学家有意设计了样品统计量的形式，以便于它们的期望正好等于某些群体参数。这能为很多统计处理带来便利。

 

统计研究的一般思路

我们一直沿着从群体到样品的思路。这就好像已经知道了整个宇宙的真相，然后再把视野局限到地球上。我们知道了群体的分布，自然很容易推导出样本取值的分布。然而，我们在生活中，往往是从样品推测群体。这就好像我们看到了一片叶子，然后去想象整个植物的样子。

 

在罐子中抽小球的问题中，群体的分布可能只有10种。我们求出其一种情况下[$X_1, X_2$]的分布，然后进行真实的抽样，看得到结果是不是符合该分布。我们假设红、蓝、黄各有一个，每次抽两个球。如果抽样100次，都没有出现一个蓝球。在三色球各有一个的情况下，这种结果出现的概率只有[$ (1/3)^{100} $]，是一个非常小的概率。因此，我们一开始的假设很可能错了。我们因此可以排除那些“猜错了”的群体分布。

 

这种类似于“穷举”的办法非常笨拙，在很多问题中完全不可行。如果群体的成员有无限多个，那么分布的情况也会有无限多种。对于连续取值，比如学校学生的身高，群体的分布也会变成无限多种。在这种情况下，统计学家只好降低期望，只研究所有可能分布中的一小部分，甚至局限于同一类分布的不同参数取值。最终的研究目标，也从完整的群体分布，降低到群体分布的一些参数，例如群体的平均值和方差。统计中很多看似复杂的数学方法，其实都是出于这一无奈的苦衷。

 

总结

到这里，我介绍了统计的基础概念：群体和样本、统计推断，并且描述了统计的研究思路。在后面的文章中，我会继续讲解统计的具体方法。我们将看到，这些统计方法，既可以解决了特定类型的问题，但也有其局限性。在数学严格性的限制下，我们不可能根据样本回答所有关于群体的问题。但了解其中的细微严格之处，也是学习统计的一大乐趣所在。

 

欢迎继续阅读“数据科学”系列文章