神经网络学习笔记 - 激活函数的作用、定义和微分证明
神经网络学习笔记 - 激活函数的作用、定义和微分证明
看到知乎上对激活函数(Activation Function)的解释。
我一下子迷失了。
因此，匆匆写下我对激活函数的理解。
激活函数被用到了什么地方
目前为止，我见到使用激活函数的地方有两个。
- 逻辑回归(Logistic Regression)
- 神经网络(Neural Network)
这两处，激活函数都用于计算一个线性函数的结果。
了解激活函数
激活函数的作用：就是将权值结果转化成分类结果。
2类的线性分类器
先说一个简单的情况 - 一个2类的线性分类器。
了解激活函数，先要明确我们的问题是："计算一个（矢量）数据的标签（分类）"。
以下图为例：
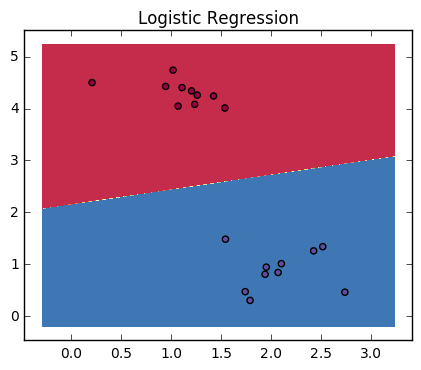
训练
训练的结果，是一组\((w,b)\)，和一个线性函数\(f(x) = wx + b\)。
预测
我们现在仔细考虑一下，如何在预测函数中使用这个线性函数\(f(x)\)。
先从几何方面理解一下，如果预测的点在分割线\(wx + b = 0\)上，那么\(f(x) = wx + b = 0\)。
如果，在分割线的上方某处，\(f(x) = wx + b = 8\)(假设是8)。
8可以认为是偏移量。
注：取决于(w, b)，在分割线上方的点可以是正的，也可能是负的。
例如： y - x =0，和 x - y = 0，这两条线实际上是一样的。
但是，应用点(1, 9)的结果， 第一个是8, 第二个是 -8。
问题
然后，你该怎么办？？？
如何用这个偏移量来得到数据的标签？
激活函数
激活函数的作用是：将8变成红色。
怎么变的呢？比如：我们使用sigmoid函数，sigmoid(8) = 0.99966464987。
sigmoid函数的结果在区间(0, 1)上。如果大于0.5，就可以认为满足条件，即是红色。
3类分类器的情况
我们再看看在一个多类分类器中，激活函数的作用。
以下图为例：
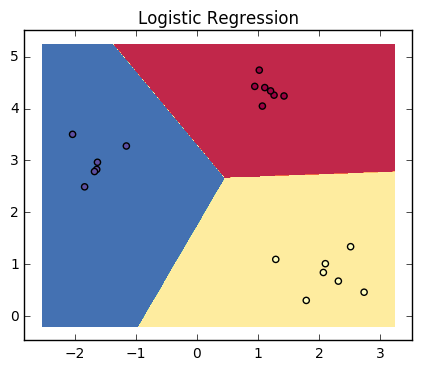
训练
3类\({a, b, c}\)分类器的训练结果是3个\((w, b)\)，三个\(f(x)\)，三条分割线。
每个\(f(x)\)，可以认为是针对一个分类的model。因此：
预测
对于预测的点\(x\)，会得到三个偏移量\([f_a(x), f_b(x), f_c(x)]\)。
使用激活函数sigmoid:
\(sigmoid([f_a(x), f_b(x), f_c(x)])\)
会得到一个向量, 记为：\([S_a, S_b, S_c]\)。
这时的处理方法是：再次使用激活函数（没想到吧）
一般会使用激活函数softmax。
激活函数，在这里的作用是：计算每个类别的可能性。
最后使用argmax函数得到：最大可能性的类。
注：上面差不多是Logistic Regression算法的一部分。
注：softmax也经常被使用于神经网络的输出层。
激活函数的来源
在学习神经网络的过程中，激活函数的灵感来自于生物神经网络，被认为是神经元对输入的激活程度。
最简单的输出形式是：一个开关，\({0, 1}\)。 要么\(0\)，要么\(1\)。
也就是一个单位阶跃函数(Heaviside step function)。
这种思想主要是一种灵感来源，并不是严格的推理。
常用的激活函数有哪些
| 名称 | 公式 | 取值范围 | 微分 | 图 |
|---|---|---|---|---|
| sigmoid - S型 |
$$
\begin{align}
\sigma(x) & = \frac{e^x}{1 + e^x} \\
& = \frac{1}{1 + e^{-x}}
\end{align}
$$
|
$(0, 1)$ |
$$
\sigma'(x) = (1 - \sigma(x))\sigma(x)
$$
|
|
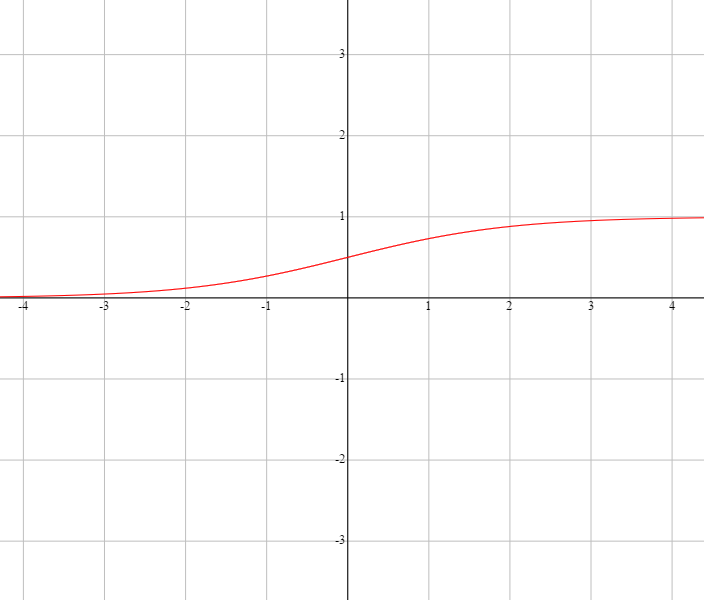
| tanh(hyperbolic tangent) - 双曲正切 |
$$
\begin{align}
tanh(x)
& = sinh(x)/cosh(x) \\
& = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\
& = \frac{e^{2x} - 1}{e^{2x} + 1} \\
& = \frac{1 - e^{-2x}}{1 + e^{-2x}}
\end{align}
$$
|
$(-1, 1)$ |
$$
tanh'(x) = 1 - tanh(x)^2
$$
|
|
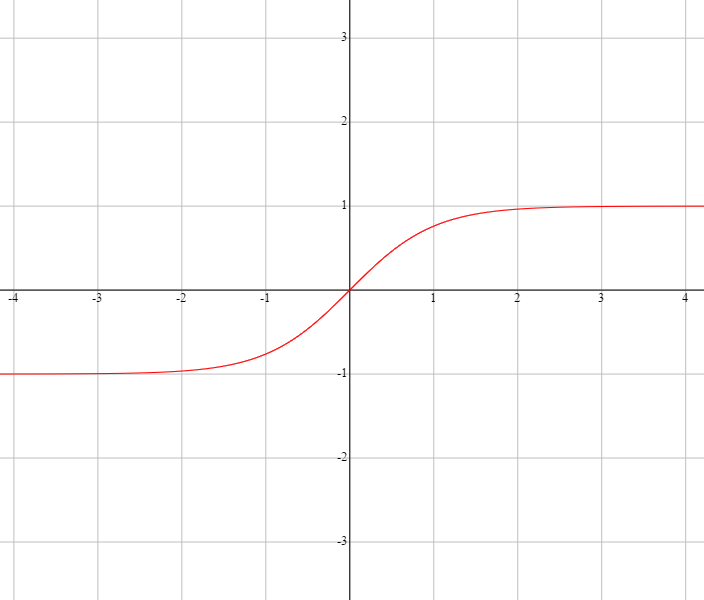
| Rectified linear unit - ReLU - 修正线性单元 |
$$
relu(x) =
\begin{cases}
0 & \text{for}\ x < 0 \\
x & \text{for}\ x \geqslant 0
\end{cases}
$$
|
$[0, \infty)$ |
$$
relu'(x) =
\begin{cases}
0 & \text{for}\ x < 0 \\
1 & \text{for}\ x \geqslant 0
\end{cases}
$$
|
|
| softmax |
$$
f(\vec{x}) = \begin{bmatrix}
\cdots &
\frac{e^{x_i}}{\sum_{k=1}^{k=K}e^{x_k}} &
\cdots
\end{bmatrix}
$$
|
$(0, 1)$ |
$$
softmax'(z_t) = \frac{\partial{y_t}}{\partial{z_t}} =
\begin{cases}
\hat{y_{t_i}}(1 - \hat{y_{t_i}}), & \text{if } i = j \\
-\hat{y_{t_i}} \hat{y_{t_j}}, & \text{if } i \ne j
\end{cases}
$$
|
激活函数的意义
| 名称 | 含义 |
|---|---|
| sigmoid - S型 |
sigmoid的区间是[0, 1]。因此，可以用于表示Yes/No这样的信息。 比如：不要(0)/要(1)。 多用于过滤数据。比如：门。 |
| tanh(hyperbolic tangent) - 双曲正切 |
tanh的区间是[-1, 1]。同样可以表示Yes/No的信息，而且加上了程度。 比如： 非常不可能(-1)/一般般(0)/非常可能(1)。 非常不喜欢(-1)/一般般(0)/非常喜欢(1)。 因此，tanh多用于输出数据。输出数据最终会使用softmax来计算可能性。 |
| softmax |
softmax用于输出层，计算每个分类的可能性。 |
| Rectified linear unit - ReLU - 修正线性单元 |
ReLU的好处：ReLU对正值较少的数据，处理能力更强。
由于，其导数为{0, 1}，可以避免梯度消失问题。
|
激活函数的微分的证明
sigmoid
sigmoid函数
证明
tanh
tanh函数
证明
softmax
激活函数softmax和损失函数会一起使用。
激活函数会根据输入的参数（一个矢量，表示每个分类的可能性），计算每个分类的概率(0, 1)。
损失函数根据softmax的计算结果\(\hat{y}\)和期望结果\(y\)，根据交叉熵方法(cross entropy loss) 可得到损失\(L\)。
softmax函数
证明
参照
请“推荐”本文！
