反向传播算法
最近看Coursera的机器学习课程,第五周讲解反向传播算法(Backpropagation Algorithm)时,部分结论没有给出推导,我这里推导一下。
1、损失函数
1.1、逻辑回归的损失函数
首先复习一下之前学过的逻辑回归的损失函数:
$J(\theta) = - \frac{1}{m} \sum_{i=1}^m [ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$
其中,$m$是样本总数。逻辑回归只有一个输出,取值是1或0。
最右边的加号,将公式分为两个部分。左侧是负log损失,可由最大似然估计得到。左侧是正则项,用以降低模型的复杂度,避免过拟合。
1.2、神经网络的损失函数
神经网络损失函数:
$J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2$
其中,$m$依然是样本总数,$K$是输出单元的个数。前面的逻辑回归只有一个输出,而神经网络可以用$K$输出,这$K$
另外,后边部分也是正则项,只是把各层的权重(每层都是个矩阵)加了起来,显得复杂。
2、计算梯度
反向传播算法就是通过训练集,使用梯度下降算法,调整各层的权重。
2.1、符号定义
$a_i^{(j)}$:第$j$层的第$i$个激活单元(activation units)
$\Theta^{(j)}$:第$j$层到$j+1$层的权重矩阵
$g(z) = \dfrac{1}{1 + e^{-z}}$:激活函数
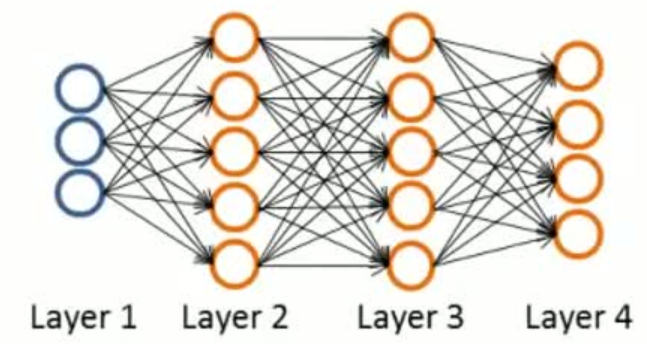
图1
如上所示的神经网络,我们的目标是求出所有的权重矩阵$\Theta^{(j)}$,使得损失函数$J(\theta)$最小。这可以通过梯度下降求解,首先要计算偏导数:
$\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}J(\Theta)$
只给一个训练样本$(x, y)$,根据前向传播算法(forward propagation):
\begin{align*}
& a^{(1)} = x \\
& z^{(2)} = \Theta^{(1)}a^{(1)} \\
& a^{(2)} = g(z^{(2)}) \quad \text(add \ a_{0}^{2}) \\
& z^{(3)} = \Theta^{(2)}a^{(2)} \\
& a^{(3)} = g(z^{(3)}) \quad \text(add \ a_{0}^{3}) \\
& z^{(4)} = \Theta^{(3)}a^{(3)} \\
& a^{(4)} = h_{\Theta}(x) = g(z^{(4)}) \\
\end{align*}
此时损失函数为:
$J(\Theta) = - \sum_{k=1}^K \left[y_k \log ((h_\Theta (x))_k) + (1 - y_k)\log (1 - (h_\Theta(x))_k)\right] + \frac{\lambda}{2}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2$
这个公式在博客园显示的有问题,${s_l}$、$s_{l+1}$中,$l$和$l+1$都是下标。再贴上一张正确显示的图片吧:
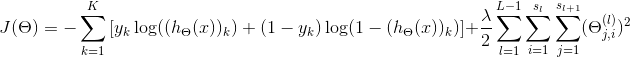
2.2、输出层权重的调整
输出层也就是$a^{(4)}$,这一步我们要调整的权重就是$\Theta^{(3)}$。图1所示的神经网络,第3层5个节点,第4层4个节点,那么$\Theta^{(3)}$就是一个$4 \times (5 + 1) $(其中,+1是因为要加上偏置的权重)的矩阵,并且有:
\begin{align*}
& a_1^{(4)} = g(\Theta_{10}^{(3)}a_0^{(3)} + \Theta_{11}^{(3)}a_1^{(3)} + \Theta_{12}^{(3)}a_2^{(3)} + \Theta_{13}^{(3)}a_3^{(3)} + \Theta_{14}^{(3)}a_4^{(3)} + \Theta_{15}^{(3)}a_5^{(3)}) \\
& a_2^{(4)} = g(\Theta_{20}^{(3)}a_0^{(3)} + \Theta_{21}^{(3)}a_1^{(3)} + \Theta_{22}^{(3)}a_2^{(3)} + \Theta_{23}^{(3)}a_3^{(3)} + \Theta_{24}^{(3)}a_4^{(3)} + \Theta_{25}^{(3)}a_5^{(3)}) \\
& a_3^{(4)} = g(\Theta_{30}^{(3)}a_0^{(3)} + \Theta_{31}^{(3)}a_1^{(3)} + \Theta_{32}^{(3)}a_2^{(3)} + \Theta_{33}^{(3)}a_3^{(3)} + \Theta_{34}^{(3)}a_4^{(3)} + \Theta_{35}^{(3)}a_5^{(3)}) \\
& a_4^{(4)} = g(\Theta_{40}^{(3)}a_0^{(3)} + \Theta_{41}^{(3)}a_1^{(3)} + \Theta_{42}^{(3)}a_2^{(3)} + \Theta_{43}^{(3)}a_3^{(3)} + \Theta_{44}^{(3)}a_4^{(3)} + \Theta_{45}^{(3)}a_5^{(3)}) \\
\end{align*}
$J(\Theta)$关于$\Theta_{ij}^{(3)}$的偏导数可以表示为:
$\dfrac{\partial}{\partial \Theta_{i,j}^{(3)}}J(\Theta)$
对正则项求导比较简单,我们先不考虑正则项,将$J(\Theta)$带入,
\begin{align*}
\dfrac{\partial}{\partial \Theta_{i,j}^{(3)}}J(\Theta) &= \dfrac{\partial}{\partial \Theta_{i,j}^{(3)}}- \sum_{k=1}^K \left[y_k \log ((h_\Theta (x))_k) + (1 - y_k)\log (1 - (h_\Theta(x))_k)\right] \\
&= \dfrac{\partial}{\partial \Theta_{i,j}^{(3)}}- \sum_{k=1}^K \left[y_k \log (a_{k}^{(4)}) + (1 - y_k)\log (1 - a_{k}^{(4)}) \right] \\
\end{align*}
在上式中,我们用到了$a_1^{(4)}$到$a_4^{(4)}$4个输出值。事实上,$\Theta_{i,j}$只有在生成$a_i^{(4)}$时才会用到。所以有:
\begin{align*}
\dfrac{\partial }{\partial \Theta_{i,j}^{(3)}}J(\Theta) &= \dfrac{\partial}{\partial \Theta_{i,j}^{(3)}}- \left[y_i \log (a_{i}^{(4)}) + (1 - y_i)\log (1 - a_{i}^{(4)}) \right] \\
&= \dfrac{\partial \left[-y_i \log (a_{i}^{(4)}) - (1 - y_i)\log (1 - a_{i}^{(4)}) \right]}{\partial a_{i}^{(4)}} \dfrac{\partial a_{i}^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
&= \left[ - y_i \frac{1}{a_{i}^{(4)}} + (1 - y_i) \frac{1}{1 - a_{i}^{(4)}} \right] \dfrac{\partial a_{i}^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
&= \frac{a_{i}^{(4)} - y_i}{a_{i}^{(4)}(1 - a_{i}^{(4)})} \dfrac{\partial a_{i}^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
&= \frac{a_{i}^{(4)} - y_i}{a_{i}^{(4)}(1 - a_{i}^{(4)})} \dfrac{\partial g(z_i^{(4)})}{\partial \Theta_{i,j}^{(3)}} \\
&= \frac{a_{i}^{(4)} - y_i}{a_{i}^{(4)}(1 - a_{i}^{(4)})} \dfrac{\partial g(z_i^{(4)})}{\partial z_i^{(4)}} \dfrac{\partial z_i^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
\end{align*}
根据$g'(z^{(l)}) = a^{(l)}\ .*\ (1 - a^{(l)})$可得:
\begin{align*}
\dfrac{\partial }{\partial \Theta_{i,j}^{(3)}}J(\Theta) &= \frac{a_{i}^{(4)} - y_i}{a_{i}^{(4)}(1 - a_{i}^{(4)})} a_{i}^{(4)}(1 - a_{i}^{(4)}) \dfrac{\partial z_i^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
&= (a_{i}^{(4)} - y_i) \dfrac{\partial z_i^{(4)}}{\partial \Theta_{i,j}^{(3)}} \\
\end{align*}
根据$z_i^{(4)} = \Theta_{i0}^{(3)}a_0^{(3)} + \Theta_{i1}^{(1)}a_1^{(3)} + \Theta_{i2}^{(1)}a_2^{(3)} + \Theta_{i3}^{(1)}a_3^{(3)} + \Theta_{i4}^{(1)}a_4^{(3)} + \Theta_{i5}^{(1)}a_5^{(3)}$,$\Theta_{i,j}^{(3)}$只与$a_j^{(3)}$有关,从而有:
\begin{align*}
\dfrac{\partial }{\partial \Theta_{i,j}^{(3)}}J(\Theta) = (a_{i}^{(4)} - y_i)a_j^{(3)}
\end{align*}
2.3、隐藏层权重的调整
这一步我们来调整$\Theta^{(2)}$。图1所示的神经网络,第2层5个节点,第3层5个节点,那么$\Theta^{(2)}$就是一个$5 \times (5 + 1) $(其中,+1是因为要加上偏置的权重)的矩阵,并且有:
\begin{align*}
& a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)} + \Theta_{14}^{(2)}a_4^{(2)} + \Theta_{15}^{(2)}a_5^{(2)}) \\
& a_2^{(3)} = g(\Theta_{20}^{(2)}a_0^{(2)} + \Theta_{21}^{(2)}a_1^{(2)} + \Theta_{22}^{(2)}a_2^{(2)} + \Theta_{23}^{(2)}a_3^{(2)} + \Theta_{24}^{(2)}a_4^{(2)} + \Theta_{25}^{(2)}a_5^{(2)}) \\
& a_3^{(3)} = g(\Theta_{30}^{(2)}a_0^{(2)} + \Theta_{31}^{(2)}a_1^{(2)} + \Theta_{32}^{(2)}a_2^{(2)} + \Theta_{33}^{(2)}a_3^{(2)} + \Theta_{34}^{(2)}a_4^{(2)} + \Theta_{35}^{(2)}a_5^{(2)}) \\
& a_4^{(3)} = g(\Theta_{40}^{(2)}a_0^{(2)} + \Theta_{41}^{(2)}a_1^{(2)} + \Theta_{42}^{(2)}a_2^{(2)} + \Theta_{43}^{(2)}a_3^{(2)} + \Theta_{44}^{(2)}a_4^{(2)} + \Theta_{45}^{(2)}a_5^{(2)}) \\
& a_5^{(3)} = g(\Theta_{50}^{(2)}a_0^{(2)} + \Theta_{51}^{(2)}a_1^{(2)} + \Theta_{52}^{(2)}a_2^{(2)} + \Theta_{53}^{(2)}a_3^{(2)} + \Theta_{54}^{(2)}a_4^{(2)} + \Theta_{55}^{(2)}a_5^{(2)}) \\
\end{align*}
同样先不考虑正则项,
\begin{align*}
\dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}J(\Theta) &= \dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}- \sum_{k=1}^K \left[y_k \log ((h_\Theta (x))_k) + (1 - y_k)\log (1 - (h_\Theta(x))_k)\right] \\
&= \dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}- \sum_{k=1}^K \left[y_k \log (a_{k}^{(4)}) + (1 - y_k)\log (1 - a_{k}^{(4)}) \right] \\
&= \sum_{k=1}^K \dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}- \left[y_k \log (a_{k}^{(4)}) + (1 - y_k)\log (1 - a_{k}^{(4)}) \right] \\
&= \sum_{k=1}^K \dfrac{\partial \left[-y_k \log (a_{k}^{(4)}) - (1 - y_k)\log (1 - a_{k}^{(4)}) \right]}{\partial a_{k}^{(4)}} \dfrac{\partial a_{k}^{(4)}}{\partial \Theta_{i,j}^{(2)}} \\
&= \sum_{k=1}^K \frac{a_{k}^{(4)} - y_k}{a_{k}^{(4)}(1 - a_{k}^{(4)})} a_{k}^{(4)}(1 - a_{k}^{(4)}) \dfrac{\partial z_{k}^{(4)}}{\partial \Theta_{i,j}^{(2)}} \\
&= \sum_{k=1}^K (a_{k}^{(4)} - y_k) \dfrac{\partial z_{k}^{(4)}}{\partial \Theta_{i,j}^{(2)}} \\
\end{align*}
接着使用复合函数的链式求导法则:
\begin{align*}
\dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}J(\Theta) &= \sum_{k=1}^K (a_{k}^{(4)} - y_k) \dfrac{\partial z_{k}^{(4)}}{\partial a_i^{(3)}} \dfrac{\partial a_i^{(3)}}{\partial \Theta_{i,j}^{(2)}} \\
&= \sum_{k=1}^K (a_{k}^{(4)} - y_k) \Theta_{kj}^{(3)} \dfrac{\partial a_i^{(3)}}{\partial \Theta_{i,j}^{(2)}} \\
&= \dfrac{\partial a_i^{(3)}}{\partial \Theta_{i,j}^{(2)}} \sum_{k=1}^K (a_{k}^{(4)} - y_k) \Theta_{kj}^{(3)} \\
&= a_i^{(3)}(1 - a_i^{(3)}) \dfrac{\partial z_i^{(3)}}{\partial \Theta_{i,j}^{(2)}} \sum_{k=1}^K (a_{k}^{(4)} - y_k) \Theta_{kj}^{(3)} \\
\end{align*}
根据$z_i^{(3)} = \Theta_{i0}^{(2)}a_0^{(2)} + \Theta_{i1}^{(2)}a_1^{(2)} + \Theta_{i2}^{(2)}a_2^{(2)} + \Theta_{i3}^{(2)}a_3^{(2)} + \Theta_{i4}^{(2)}a_4^{(2)} + \Theta_{i5}^{(2)}a_5^{(2)}$,
\begin{align*}
\dfrac{\partial}{\partial \Theta_{i,j}^{(2)}}J(\Theta) &= a_i^{(3)}(1 - a_i^{(3)}) a_j^{(2)} \sum_{k=1}^K (a_{k}^{(4)} - y_k) \Theta_{kj}^{(3)} \\
\end{align*}
同样的,根据链式求导法则,可以计算$\dfrac{\partial}{\partial \Theta_{i,j}^{(1)}}J(\Theta)$。
2.4、结论
对于$L$层的神经网络(图1我们认为有4层),记:
$\delta^{(L)} = a^{(L)} - y^{(t)}$ (注意,这是向量)
$\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)})\ .*\ a^{(l)}\ .*\ (1 - a^{(l)})$ 对于$0 < l < L$
则:$\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}J(\Theta) = a_j^{(l)} \delta_i^{(l+1)}$
参考文献:
Coursera:机器学习第五周课程
码农场hancks:反向传播神经网络极简入门


