【杜教筛】学习笔记
思路
普通杜教筛
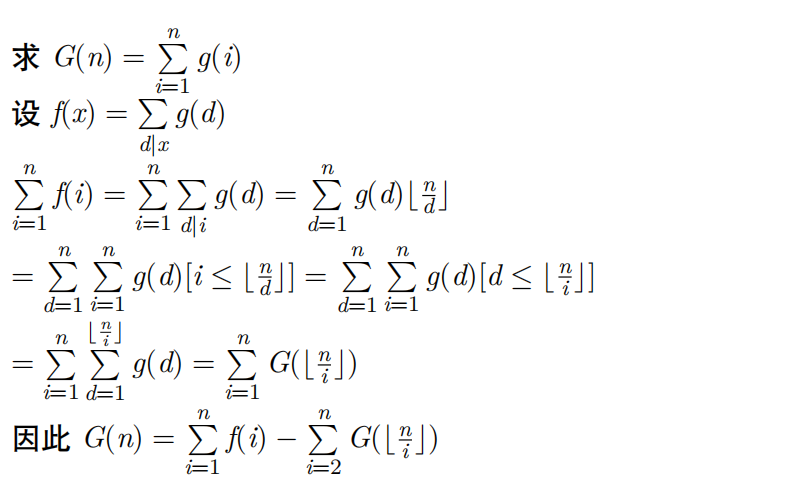
扩展杜教筛

代码
普通杜教筛(BZOJ3944 sum)
//by 减维 #include<set> #include<map> #include<queue> #include<ctime> #include<cmath> #include<bitset> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define ll long long #define il inline #define rg register #define db double #define mpr make_pair #define maxn 5000005 #define inf (1<<30) #define eps 1e-8 #define pi 3.1415926535897932384626L using namespace std; inline int read() { int ret=0;bool fla=0;char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-')ch=getchar(); if(ch=='-'){fla=1;ch=getchar();} while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();} return fla?-ret:ret; } ll t,n,tot,pri[maxn/10],phi[maxn],mu[maxn],q[maxn/10],p[maxn/10]; bool pd[maxn],vis[maxn]; void pre(ll x) { pd[1]=1;phi[1]=1;mu[1]=1; for(rg ll i=2;i<=x;++i) { if(!pd[i]) pri[++tot]=i,phi[i]=i-1,mu[i]=-1; for(rg int j=1;j<=tot&&i*pri[j]<=x;++j) { pd[pri[j]*i]=1; if(i%pri[j]==0) { phi[i*pri[j]]=phi[i]*pri[j]; mu[i*pri[j]]=0; break ; } phi[i*pri[j]]=phi[i]*phi[pri[j]]; mu[i*pri[j]]=-mu[i]; } } for(rg int i=2;i<=x;++i) phi[i]+=phi[i-1],mu[i]+=mu[i-1]; } il ll getp(ll x){return x<=maxn-5?phi[x]:p[n/x];} il ll getq(ll x){return x<=maxn-5?mu[x]:q[n/x];} void solve(ll x) { if(x<=5000000) return ; if(vis[n/x]) return ; vis[n/x]=1; p[n/x]=x*(x+1)/2; q[n/x]=1; for(rg ll i=2,las;i<=x;i=las+1) { las=x/(x/i);solve(x/i); p[n/x]-=(las-i+1)*getp(x/i); q[n/x]-=(las-i+1)*getq(x/i); } } int main() { scanf("%lld",&t); pre(5000000); while(t--) { scanf("%lld",&n); memset(vis,0,sizeof vis); solve(n); printf("%lld %lld\n",getp(n),getq(n)); } return 0; }
扩展杜教筛(51nod1237 最小公倍数之和 V3)
//by 减维 #include<set> #include<map> #include<queue> #include<ctime> #include<cmath> #include<bitset> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define ll long long #define il inline #define rg register #define db double #define mpr make_pair #define maxn 5000005 #define inf (1<<30) #define eps 1e-8 #define pi 3.1415926535897932384626L #define mod 1000000007 using namespace std; inline int read() { int ret=0;bool fla=0;char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-')ch=getchar(); if(ch=='-'){fla=1;ch=getchar();} while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();} return fla?-ret:ret; } ll n,p,tot,inv2,inv6,pri[maxn],phi[maxn]; bool pd[maxn]; map<ll,ll> mp; ll ksm(ll x,ll y) { ll ret=1; while(y) { if(y&1) ret=ret*x%p; x=x*x%p; y>>=1; } return ret; } void pre(ll x) { phi[1]=1; for(ll i=2;i<=x;++i) { if(!pd[i]) pri[++tot]=i,phi[i]=(i-1)%p; for(int j=1;j<=tot&&i*pri[j]<=x;++j) { pd[i*pri[j]]=1; if(i%pri[j]==0) { phi[i*pri[j]]=(phi[i]*pri[j])%p; break ; } phi[i*pri[j]]=(phi[i]*phi[pri[j]])%p; } } for(ll i=1;i<=x;++i) phi[i]=phi[i]*i%p*i%p; for(ll i=1;i<=x;++i) phi[i]=(phi[i]+phi[i-1])%p; inv2=ksm(2,p-2); inv6=ksm(6,p-2); } ll f(ll x) { return ((x%p)*((x+1)%p)%p*inv2%p)*((x%p)*((x+1)%p)%p*inv2%p)%p; } ll ff(ll x) { return (x%p)*((x+1)%p)%p*inv2%p; } ll pf(ll x) { return (x%p)*((x%p+1)%p)%p*((2*x%p+1)%p)%p*inv6%p; } ll getji(ll x) { if(x<=maxn-5) return phi[x]; if(mp[x]) return mp[x]; ll ret=f(x); for(ll l=2,r;l<=x;l=r+1) { r=x/(x/l); ret-=(pf(r)%p-pf(l-1)%p+p)%p*getji(x/l)%p; ret%=p;ret+=p;ret%=p; } return mp[x]=ret; } ll solve() { ll ret=0; for(ll l=1,r;l<=n;l=r+1) { r=n/(n/l); ret+=ff(n/l)*((getji(r)-getji(l-1)+p)%p)%p; ret%=p; } return ret; } int main() { scanf("%lld",&n);p=1000000007; pre(maxn-5); printf("%lld",solve()); return 0; }



