【三分模板】洛谷P3382三分模板
题目描述
如题,给出一个N次函数,保证在范围[l,r]内存在一点x,使得[l,x]上单调增,[x,r]上单调减。试求出x的值。
输入输出格式
输入格式:
第一行一次包含一个正整数N和两个实数l、r,含义如题目描述所示。
第二行包含N+1个实数,从高到低依次表示该N次函数各项的系数。
输出格式:
输出为一行,包含一个实数,即为x的值。四舍五入保留5位小数。
输入输出样例
输入样例#1:
3 -0.9981 0.5 1 -3 -3 1
输出样例#1:
-0.41421
说明
时空限制:50ms,128M
数据规模:
对于100%的数据:7<=N<=13
样例说明:
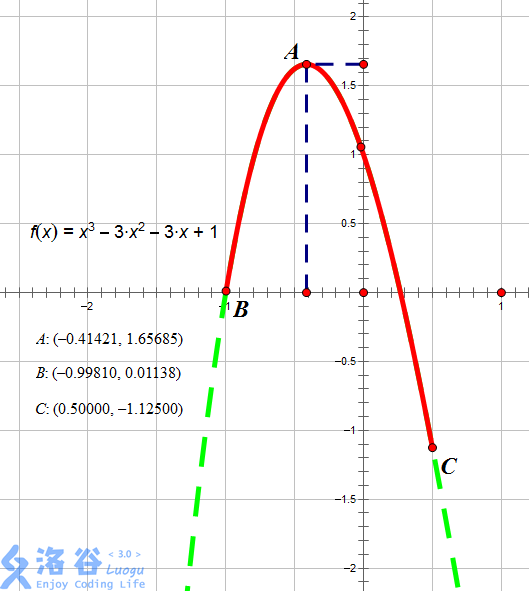
如图所示,红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。
当x=-0.41421时图像位于最高点,故此时函数在[l,x]上单调增,[x,r]上单调减,故x=-0.41421,输出-0.41421。
题解:
显然这是一道模板题。。。
代码如下:
#include<cstdio> #include<iostream> using namespace std; double n,l,r,a[15]; double pd(double x) { double b=a[1]*x; for(int i=2;i<=n;++i) b=(b+a[i])*x; return b; } int main() { scanf("%lf%lf%lf",&n,&l,&r); for(int i=1;i<=n;++i)scanf("%lf",&a[i]); while(r-l>1e-6) { double lm,rm; lm=(2*l+r)/3; rm=(l+2*r)/3; if(pd(lm)>pd(rm))r=rm; else l=lm; } printf("%.5lf",l); }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号