二叉索引树BIT
定义
二叉索引树,binary index tree,又名树状数组,或Fenwick Tree,因为本算法由Fenwick创造。
对于数组A,定义Query(i,j) = Ai +Ai+1 + … + Aj.
比较好的做法:使用前缀和,Sum(j) – Sum(i-1)即可得到Query(i,j)
BIT即为解决此类区间查询而大展身手,因为预处理时间为O(n),之后的查询时间为O(1),是属于典型的在线算法(关于在线算法,通俗地可以理解为,做一次预处理,提供多次“服务”——比如多次Query(i,j))。
Lowbit(nature)
首先,定位lowbit(natural)为自然数(即1,2,3…n)的二进制形式中最右边出现1的值。
比如:4 = 100,lowbit(4) = 4;36 = 100100,lowbit(36) = 4.
自然数在二进制形式下,有如下的性质:
Lowbit为1的自然数为1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31…d = 2
Lowbit为2的自然数为2,6,10,14,18,22,26,30,… d = 4
Lowbit为3的自然数为4,12,20,28… d=8
Lowbit为4的自然数为8,32
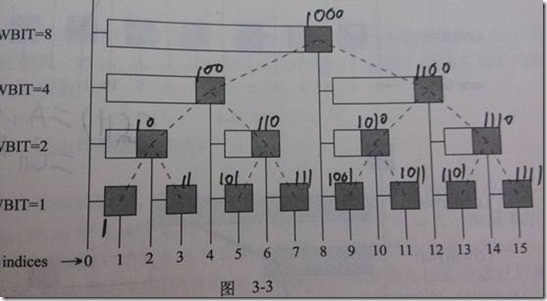
直接上刘汝佳的算法竞赛入门竞赛经典中的图片:
树状性质:对于节点i,如果他是左子结点,那么父节点的编号就是i+lowbit(i);如果它是右子节点,那么父节点的编号是i-lowbit(i)。
令数组C为:
Ci = Ai-lowbit(i)+1+A i-lowbit(i)+2+…Ai
即从最左边的孩子,到自身的和,如C12 = A9(上图中最左边的儿子)+A10+A11+A12,C6=A5+A6。
计算前缀和Sum(i)的计算:
顺着节点i往左走,边走边“往上爬”,把经过的Ci 累加起来即可。
API
l lowbit(idx)
求A[idx]的低位
l Sum(i)
求区间1,i的前缀和
l Add(idx,value)
使节点idx的值增加value;
代码:
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace Algorithms.Data_Structure { /// <summary> /// 二叉索引树(树状数组:Fenwick Tree) /// </summary> public class BinaryIndexedTree { /// <summary> /// 处理的数组 /// </summary> private List<int> array; /// <summary> /// 二叉前缀和 /// </summary> private List<int> tree; /// <summary> /// 个数 /// </summary> private int n; public BinaryIndexedTree(int[] array) { this.array = new List<int>(array); this.n = this.array.Count; PreProcessing(); } /// <summary> /// 预处理函数:每次增加数值 /// </summary> private void PreProcessing() { tree = new List<int>(n); for (int ii = 0; ii < n; ii++) { tree.Add(0); } for (int ii = 1; ii < n; ii++) { Update(ii, array[ii]); } } /// <summary> /// 二进制形式中的最右边的1所对应的值,如38288 = 1001010110010000 ,则返回16 /// </summary> /// <param name="idx"></param> private int lowbit(int idx) { return idx & (-idx); } /// <summary> /// 在x处加v /// </summary> /// <param name="idx">数组的索引,从1开始计数</param> /// <param name="v">值</param> public void Update(int idx, int v) { while (idx < n) { tree[idx] += v; idx += lowbit(idx); //left's parent } } /// <summary> /// 从0到x求和 /// </summary> /// <param name="idx">索引,从1开始计数</param> /// <returns>求和结果</returns> public int Sum(int idx) { int ret = 0; while (idx > 0) { ret += tree[idx]; idx -= lowbit(idx); // right's parent } return ret; } } }
Test:
class Program { static void Main(string[] args) { BinaryIndexedTree bit = new BinaryIndexedTree(new int[] { 0, 1, 2, 3, 4, 5 }); //从1开始计数 Console.WriteLine(bit.Sum(5));//15 bit.Update(4, 23); Console.WriteLine(bit.Sum(5));//38 } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号