无约束优化方法(梯度法-牛顿法-BFGS- L-BFGS)
本文讲解的是无约束优化中几个常见的基于梯度的方法,主要有梯度下降与牛顿方法、BFGS 与 L-BFGS 算法。
梯度下降法是基于目标函数梯度的,算法的收敛速度是线性的,并且当问题是病态时或者问题规模较大时,收敛速度尤其慢(几乎不适用);
牛顿法是基于目标函数的二阶导数(Hesse 矩阵)的,其收敛速度较快,迭代次数较少,尤其是在最优值附近时,收敛速度是二次的。但牛顿法的问题在于当海森矩阵稠密时,每次迭代的计算量比较大,因为每次都会计算目标函数的海森矩阵的逆,这样一来,当数据维度较高时,不仅计算量大(有时大到不可计算),而且需要的存储空间也多,因此牛顿法在面对海量数据时由于每一步迭代的开销巨大而变得不适用。
拟牛顿法是在牛顿法的基础上引入了海森矩阵的近似矩阵,避免每次迭代都要计算海森矩阵的逆,拟牛顿法的收敛速度介于梯度下降法和牛顿法之间,是超线性的。拟牛顿法的问题也是当问题规模很大时,近似矩阵变得很稠密,在计算和存储上也有很大的开销,因此变得不实用。
另外需要注意的是,牛顿法在每次迭代时不能总是保证海森矩阵是正定的,一旦海森矩阵不是正定的,优化方向就会“跑偏”,从而使得牛顿法失效,也说明了牛顿法的鲁棒性较差。拟牛顿法用海森矩阵的逆矩阵来替代海森矩阵,虽然每次迭代不能保证是最优的优化方向,但是近似矩阵始终是正定的,因此算法总是朝着最优值的方向在搜索。这些方法均是基于迭代的方法,通过找到序列 $x_1,x_2,….x_k,…$ 来一步步极小化目标函数,达到求取极小值的目的。
大概了解了各种算法的特点之后,接下来步入正文,对于无约束优化问题,变量 $x \in \mathbb{R}^n$ ,目标函数为:
\[\min_xf(x)\]
泰勒级数
基于梯度的方法都会涉及泰勒级数问题,这里简单介绍一下,泰勒级数就是说函数 $f(x)$ 在点 $x_0$ 的邻域内具有 $n+1$ 阶导数,则该邻域内 $f(x)$ 可展开为 $n$ 阶泰勒级数为:
\[f(x) = f(x_0) + \nabla f(x_0)(x-x_0)+\frac{\nabla^2f(x_0)}{2!}(x-x_0)^2+…+\frac{\nabla^nf(x_0)}{n!}(x-x_0)^n\]
梯度下降法
梯度下降法是一种通过迭代来求取极值的方法,它使用目标函数的一阶导数信息,每次迭代取目标函数值下降最快的方向作为搜索方向,目标函数 $f(x)$ 在什么方向下降最快呢?这里给出一个证明,假设当前为第 $k$ 次迭,在自变量取值 $x_k$ 处进行泰勒展开可得:
\[f(x) = f(x_k) + \nabla f(x_k)(x-x_k)\]
这里严格意义上应该取 “ $\approx$ ” 因为只取了一阶泰勒,之后的牛顿法,展开为二阶泰勒也是近似相等的关系。现在 $f(x)$ 即为下一步的取值的函数,将 $x – x_k $ 即为下一步要迭代的方向,记做 $ag$,意思是说 $x$ 沿单位向量 $g \in \mathbb{R}^n$ 的方向迭代,$\alpha$ 为步长参数记 ,代表走多大的一步,现在一阶泰勒可写作:
\[f(x_k) – f(x) = – \alpha \nabla f(x_k) \cdot g \]
每次迭代是为了使目标函数尽可能减小,即使得 $f(x_k) – f(x)$ 尽可能大,忽略步长参数 $\alpha$, 可得极大化 $f(x_k) – f(x)$ 等价于:
\[ \min \nabla f(x_k) \cdot g\]
$\nabla f(x) \cdot g$ 代表两向量的乘积,很明显,两向量方向相反时便能取得最小值,所以要想使得迭代后以目标函数以最快速度下降,迭代的方向 $g$ 应该是梯度的反方向, $x$ 每次沿着 $-\nabla f(x)$ 的方向前进便能得到极小值,综上梯度下降的算法如下:
\[x^{k+1} := x^{k} – \alpha \nabla f(x_k)\]
负梯度是下降最快的方向,梯度是上升最快的方向,证明就是上述的很简单的一个泰勒展开。
牛顿方法
牛顿方法也是一种迭代的方法,不同于梯度下降,该方法引入了二阶导数信息,假设当前迭代到第 $k$ 次,将目标函数在自变量 $x_k$ 处展开为二阶泰勒级数:
\[ f(x) = f(x_k) + \nabla f(x_k) (x-x_k)+ \frac{1}{2} (x –x_k)^T\nabla^2 f(x_k )(x-x_k)\]
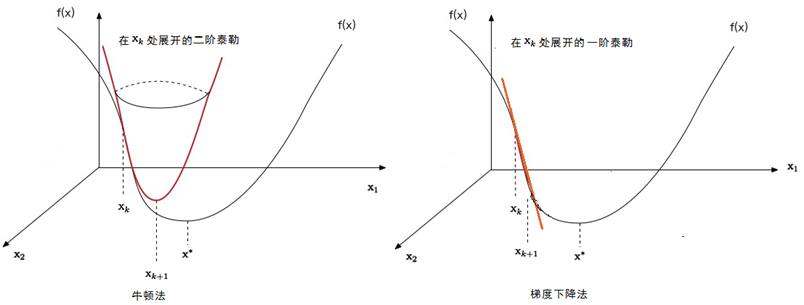
在这个关于 $x$ 的二次函数里,另其导数得 $0$ ,得到的点即可作为下一次自变量的值 $x_{k+1}$,人们常说的牛顿方法是曲面拟合,这个曲面正是关于 $x$ 的二次函数构成的,而在梯度法中由于一阶泰勒只用到 $x$ 的一次函数,所以梯度法是平面拟合,下图展示了牛顿法与梯度法的区别:
接下来对 $f(x)$ 两端同时对 $x$ 求导,另导数得零求得的极值点就是下一次迭代的取值 $x_{k+1}$:
\[\nabla f(x) = \nabla f(x_k) + \nabla^2 f(x_k )(x-x_k) = 0 \]
公式里的 $\nabla f$ 为梯度 ,$\nabla^2 f$ 为 Hesse 矩阵,方便起见,将 $\nabla f$ 记做 $g$ ,$\nabla^2 f$ 记做 $H$ , $g$ 与 $H$ 的形式分别如下:
\[ g = \nabla f = \begin{bmatrix} \frac{\partial f }{\partial x_1} \\ \frac{\partial f }{\partial x_2} \\ \vdots\\\frac{\partial f }{\partial x_n} \\ \end{bmatrix} \ \ \ \
H = \nabla^2 f = \begin{bmatrix}
\frac{\partial^2 f }{\partial^2 x_1}& \frac{\partial^2 f }{\partial x_1 x_2} & \cdots &\frac{\partial ^2 f }{\partial x_1x_n} \\
\frac{\partial^2 f }{\partial^2 x_1x_2}& \frac{\partial^2 f }{\partial x_2^2} &\cdots &\frac{\partial ^2 f }{\partial x_2x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f }{\partial^2 x_nx_1}& \frac{\partial^2 f }{\partial x_n x_2} &\cdots &\frac{\partial ^2 f }{\partial x_n^2} \\
\end{bmatrix} \]
采用符号 $g$ 与 $H$ 表示:
\[g_k + H_k(x-x_k) = 0\]
综上于是 $x$ 在下一次迭代的取值 :
\[x_{k+1} = x_k -H^{-1}_k g_k \]
这里 $-H^{-1}_k g_k$ 即为搜索方向向量,函数值需要在此方向下降,所以需要与梯度 $g_k$ 反向 ,即 $-g_kH^{-1}_k g_k<0$ ,显而易见需要 Hesse 矩阵是正定的。如果这一条件不满足,可能导致目标函数不一定下降,从而牛顿法不收敛。比如说初始点 $x_0$ 离极小值点比较远,就可能造成其 Hesse 矩阵不是正定的,甚至是正定,但目标函数值没有下降。对于二次型函数,牛顿法一次迭代便可达到极值点,但对于非二次型,牛顿法缺少步长因子,所以迭代可能导致发散或者不稳定的现象,所以在迭代时,需要在每一步迭代时给出一个步长参数 $\lambda_k$:
\[ \lambda_k = arg \min_{\lambda} f(x_k – \lambda H_k^{-1}g_k)\]
综上,总结一下牛顿法的特点:
- 牛顿法每次计算都需要计算目标函数的 Hesse 矩阵,计算量非常大,且要求 Hesse矩阵正定;
- 梯度下降法是一阶收敛,牛顿法是二阶收敛,由于二阶导 $\Delta (x_k)$ 可能为0甚至为负(非正定),则迭代后的 $x_{k+1}$ 可能不是下降方向(如果为0,则无法计算)。
- 牛顿法是用一个二次曲面去拟合当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部平面,所以牛顿法选择的下降路经会更符合真实的最优下降路经;
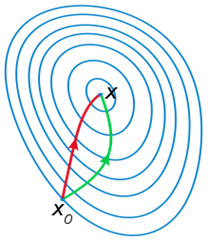
下图来自 wiki ,红色的为牛顿法,搜索方向明显优于地图下降法绿线:
拟牛顿法
拟牛顿法可以克服牛顿法计算量大的缺点,不在计算目标函数的 Hesse 矩阵,而是构造一个近似 Hesse 矩阵的对称正定矩阵,根据近似矩阵来优化目标函数,不同的近似构造 Hesse 的方法决定了不同的拟牛顿法,构造 Hesse 矩阵是需要满足拟牛顿条件的,拟牛顿条件是这样求得的,首先将 $f(x)$ 在 $x_{k+1}$ 处做二阶泰勒展开:
\[ f(x) = f(x_{k+1}) + \nabla f(x_{k+1}) (x-x_{k+1})+ \frac{1}{2} (x –x_{k+1})^T\nabla^2 f(x_{k+1} )(x-x_{k+1})\]
两边同时对 $x_{k+1}$求导可得:
\[g = g_{k+1}+ H_{k+1}(x -x_{k+1}) \]
令 $x = x_k$ ,整理可得:
\[ g_{k+1} – g_k = H_{k+1} (x_{k+1} – x_k)\]
这个便是拟牛顿条件了,迭代过程中对 $H_{k+1}$ 做出约束,根据约束构造一个近似矩阵 $B_{k+1}$ ,来模拟 Hesse 矩阵就可以了,为了简便起见,引入记号 $s_k$ 与 $y_k$ :
\[ s_k = x_{k+1} –x_k , y_k = g_{k+1} –g _k \]
因此可得拟牛顿条件为:
\[ y_k = B_{k+1} \cdot s_k \]
因为牛顿法中的迭代方向为 $-H^{-1} \cdot g$,所以另 D_{k+1} = H_{k+1}^{-1},拟牛顿条件还可以写作:
\[s_k = D_{k+1} \cdot y_k \]
BFGS
BFGS 是一种拟牛顿方法,通过迭代构建近似 Hesse 矩阵,省去了求解 Hesse 的复杂的步骤,而且 BFGS 构造出来的近似 Hesse 矩阵一定是正定的,这完全克服了牛顿法的缺陷,虽然搜索方向不一定最优,但始终朝着最优的方向前进的。首先初始化 Hesse 矩阵 $B_0 = I $ ,接下来每次迭代对矩阵 $B_k$ 进行更新即可:
\[ B_{k+1} = B_k+ \Delta B_k , \ k = 1,2,…\]
迭代构建近似矩阵的关键是矩阵 $\Delta B_k$ 的构造了,将其写作:
\[\Delta B_k = \alpha uu^T + \beta vv^T\]
这里的向量 u 和 v 是待定的,知道了这两个向量,就可以构造构造 $\Delta B_k$ 了,且这样构造出的矩阵是对称的,根据拟牛顿条件:
\begin{aligned}
y_k &= B_{k+1} s_k \\
&= (B_k + \Delta B_k)s_k \\
&= (B_k + \alpha uu^T + \beta vv^T)s_k \\
&= B_k s_k + (\alpha u^Ts_k) \cdot u+ (\beta v^Ts_k) \cdot v
\end{aligned}
这里 $\alpha u^Ts_k$ 与 $\beta v^Ts_k$ 均为实数,代表了 在 $u$ 与 $v$ 方向的拉伸程度,为了计算简单,做如下赋值运算:
\[\alpha u^Ts_k = 1 , \ \beta v^Ts_k = –1\]
代入上式便可得:
\[u - v = y_k – B_ks_k\]
这就得到得到了 $u$ 与 $v$ 的一个近似:
\[ u = y_k , \ v = B_k s_k\]
继而求 $\alpha$ 与 $\beta$ 的值,下式推倒中用了$B_k$ 对称的特征:
\[\alpha = \frac{1}{y^Ts_k}, \beta= -\frac{1}{(B_ks_k)^Ts_k} = -\frac{1}{s_k^TB_ks_k}\]
$\alpha$ 、 $\beta$ 、 $u$ 与 $v$都求得后,便得到了 $\Delta B_k$ 的更新公式:
\[\Delta B_k = \frac{y_ky_k^T}{y_k^Ts_k} – \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k}\]
因此迭代计算的公司为:
\[B_{k+1} = B_k +\frac{y_ky_k^T}{y_k^Ts_k} – \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k}\]
由与牛顿法的方向是 $–H^{-1}_kg_k$ 的,所以最好可以直接计算出 $B_k^{-1}$ ,这样就不用再进行求逆运算了,直接根据Sherman-Morrison 公式:可得关于矩阵B 的逆的更新方式:
\[B^{-1}_{k+1} = B^{-1}_k + \left (\frac{1}{s_k^Ty_k}+\frac{y_k^TB_k^{-1}y_k}{(s_k^Ty_k)^2} \right )s_ks_k^T - \frac{1}{s_k^Ty_k} \left (B_k^{-1}y_ks_k^T + s_ky_k^TB^{-1}_k \right)\]
$B^{-1}_k$ 不就是 $D_k$ 吗,这里用 $D_k$ 来表示,给出最终的 BFGS 算法:
1. 给出 $x_0$ 与迭代停止条件 ,另 $D_0 = I, \ k = 0$;
2. $for$ $k = 1,2,…K$, $do$:
2.1 牛顿法的搜索方向为 $d_k = – D_kg_k$
2.2 依照牛顿方法计算步长因子 $\lambda_k$:\[s_k = -\lambda_k d_k, \ \ x_{k+1} = x_k + s_k\]
2.3 满足条件则停止迭代
2.4 计算 $y_k = g_{k+1} – g_k$
2.6 更新拟Hesse 矩阵:
\[D_{k+1} = D_k + \left (\frac{1}{s_k^Ty_k}+\frac{y_k^T D_ky_k}{(s_k^Ty_k)^2} \right )s_ks_k^T - \frac{1}{s_k^Ty_k}(D_ky_ks_k^T + s_ky_k^T D_k )\]
这就是全部的 BFGS 算法了
停止条件为人为设定,可设定为两次迭代目标函数差的阈值或者梯度差的阈值,或者梯度本身作为阈值。
L-BFGS
工业中实用的拟牛顿法的便是 L-BFGS 了,以前一直只听说过它的大名,其实就是一种拟牛顿方法而已,这里也不细看了,对于近似 Hesse 矩阵 $D_k$ :
\[D_{k+1} = D_k + \left (\frac{1}{s_k^Ty_k}+\frac{y_k^T D_ky_k}{(s_k^Ty_k)^2} \right )s_ks_k^T - \frac{1}{s_k^Ty_k}(D_ky_ks_k^T + s_ky_k^T D_k )\]
而是存储向量序 $s_k,y_k$,而且向量序列也不是都存,而是存最近的 $m$ 次的, $m$ 为人工指定,计算 $D_k$ 时,只用最新的 $m$ 个向量模拟计算即可。在第 k 次迭代,算法求得了 $x_k$ ,并且保存的曲率信息为 ${s_i, y_i}_{k-m}^{k-1}$。为了得到 $H_k$,算法每次迭代均需选择一个初始的矩阵 $H_K^0$,这是不同于 BFGS 算法的一个地方,接下来只用最近的 m 个向量对该初始矩阵进行修正,实践中 $H_k^0$ 的设定通常如下:
\begin{aligned}
H_k^0 &=r_kI \\
r_k &=\frac{s{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}}
\end{aligned}
其中 $r_k$ 表示比例系数,它利用最近一次的曲率信息来估计真实海森矩阵的大小,这就使得当前步的搜索方向较为理想,而不至于跑得“太偏”,这样就省去了步长搜索的步骤,节省了时间。在L-BFGS算法中,通过保存最近 m 次的曲率信息来更新近似矩阵的这种方法在实践中是很有效的,虽然 L-BFGS 算法是线性收敛,但是每次迭代的开销非常小,因此 L-BFGS 算法执行速度还是很快的,而且由于每一步迭代都能保证近似矩阵的正定,因此算法的鲁棒性还是很强的。
总结下 BFGS 与 L-BFGS 的: BFGS算法在运行的时候,每一步迭代都需要保存一个 $n \times n$ 的矩阵,现在很多机器学习问题都是高维的,当 $n$ 很大的时候,这个矩阵占用的内存是非常惊人的,并且所需的计算量也是很大的,这使得传统的 BFGS 算法变得非常不适用。而 L-BFGS 则是很对这个问题的改进版,从上面所说可知,BFGS 算法是通过曲率信息 $(sk, yk)$ 来修正 $H_k$ 从而得到 $Hk+1$ ,L-BFGS 算法的主要思路是:算法仅仅保存最近 $m$ 次迭代的曲率信息来计算 $H_{k+1}$ 。这样,我们所需的存储空间就从 $n \times n$ 变成了 $2 m \times n$ 而通常情况下 $m<<n$ 。
参考文献:
http://tangxman.github.io/2015/11/19/optimize-newton/
http://www.cnblogs.com/richqian/p/4535550.html
http://www.cnblogs.com/zhangchaoyang/articles/2600491.html
http://mlworks.cn/posts/introduction-to-l-bfgs/
http://blog.csdn.net/itplus/article/details/21896981
http://blog.csdn.net/henryczj/article/details/41542049
http://www.voidcn.com/blog/dadouyawp/article/p-4204403.html 很棒的文章