机器学习公开课备忘录（五）无监督学习

机器学习公开课备忘录（五）无监督学习

对应公开课八九周内容，备忘录整理的是偏向算法类的思想内容，因此第10周的照片OCR系统没有做总结，第九周的推荐系统也未做总结

一、K-means聚类算法

算法步骤

1. 设定n个聚类中心
2. 簇分配（Cluster Assignment）:每个数据点\(x^{(i)}\)划分到离它最近的聚类中心的那一类中，即\(c^{(i)}=\min\limits_k||x^{(i)}-\mu_k||^2\)
3. 聚类中心更新：将每个聚类的中心\(U_k\)位置更新为该类中所有数据点的平均值
4. 重复步骤2~3，直到聚类中心不再变化

算法理解与使用

1. K-means的代价函数为：$$J(c^{{(1)},\ldots,c},\mu_1,\ldots,\mu_K)=\frac{1}{m}\sum\limits_{i=1}^{m}||x-\mu_{c^{(i)}}||2$$
簇分配本质上是在不断最小化\(J\)的过程
2. 使用算法时，可以直接挑选K个样本为初始聚类中心进行更新，为了防止偶然性，可以多次初始化（该方法对K=2~10有较好效果）
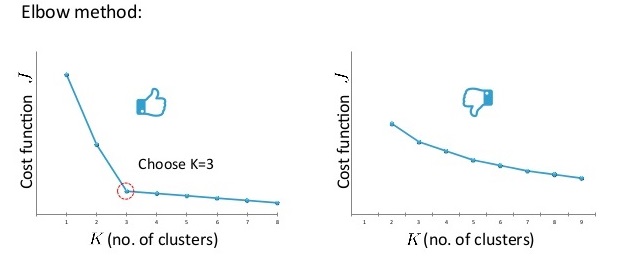
3. K的选择可以依赖肘部法则（即绘制J随K变化的曲线，选择下降速度突然减小的点）或者现实考虑（如某种衣服要划分K个型号）：

二、PCA降维（主成份分析）

PCA的思路

当二维数据点近似分布在一条直线上时，可以将其用一个变量代替，同理，多维可以降到更低维。该思路可以用于数据降维减少计算量或数据可视化。
PCA降维的依据就是误差最小化，误差是指数据点到到降维后超平面的投射距离，以二维数据为例：

蓝色点为原数据点，红色点为近似后的数据点，黑色细线即为PCA过程中产生的误差。
（注意到这里的误差是投影点直接的距离，和线性回归的误差是不同的）

PCA算法步骤

1. feature scaling：\(x_j^{(i)}=\frac{x^{(i)}-\mu_j}{\sigma_j}\)
2. 计算协方差矩阵：$$\Sigma=\frac{1}{m}\sum\limits_{i=1}^{m}x(x^{(i)})T \quad $$
3. 计算协方差矩阵\(\sum\)的特征向量：

[U,S,V] = svd(Sigma)

4. 选举U矩阵的前k个列向量组成\(U_{reduce}\)
5. 计算降维后的数据：\(z = U_{reduce}^Tx\)(也可以利用该矩阵还原数据)

PCA算法的使用

1. k值的选择，可以依据根据投射误差与原数据的范数平方的平均值之比得到，例如：$$\frac{\frac{1}{m}\sum\limits_{i=1}^{m}||x-x^{{(i)}_{approx}||}2}{\frac{1}{m}\sum\limits_{i=1}^{m}||x||^2} \leq 0.01(0.05)$$
就说明误差占比例小于1%，也就是说保留了99%的差异性
2. 因此，选择k可以从k=1开始循环，直到寻找的k满足差异性条件
3. PCA减少了特征，但没有减少特征的信息量，无法用于过拟合
4. 在使用PCA加快系统求解速度前，要用原始数据验证模型准确性

三、异常检测

异常检测针对的是有少量\((0-20)\)正例\((y=1)\)的情况，此时由于正例太少，若使用监督学习则无法学习到足够的内容。
异常检测的核心思路就是利用训练数据建模\(p(x)\)，若新的数据点满足\(p(x_{new} < \epsilon)\)，即发生概率过小，则认为该点异常

异常检测算法

假设\(x的分布符合高斯分布，则\):

\[p(x;\mu, \sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2}) \]

其中：$$\mu = \frac{1}{m}\sum\limits_{i=1}^{m}x,\sigma^{2=\frac{1}{m}\sum\limits_{i=1}}(x^{(i)}-\mu)2$$
统计学中，有时候也选用\(\frac{1}{m-1}\)的系数
对于多特征的训练集，可以假设每个特征都符合高斯分布，且独立同分布，最后的概率就为：

\[\begin{align*}p(x)&=p(x_1; \mu_1, \sigma_1^2)p(x_2; \mu_2, \sigma_2^2)\ldots p(x_n; \mu_n, \sigma_n^2) \\ &= \prod\limits_{j=1}^n p(x_j; \mu_j, \sigma_j^2)\end{align*} \]

其中：$$\mu_j = \frac{1}{m}\sum\limits_{i=1}^{m}x_j,\sigma^{2_j=\frac{1}{m}\sum\limits_{i=1}}(x^{{(i)}_j-\mu_j)}2$$
最后，阈值的选取可以根据交叉验证集的表现来确定。即通过不同的阈值，来计算对应的验证集的查准率、召回率或\(F1\)值等

多元高斯分布

多元高斯分布解决的是各个特征之间不独立的情况，此时有公式：

\[p(x;\mu, \Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right) \]

其中：$$\mu=\frac{1}{m}\sum\limits_{i=1}^{m}x,\Sigma=\frac{1}{m}\sum\limits_{i=1}^{m}(x-\mu)(x^{(i)}-\mu)T$$
当协方差矩阵是对角阵且对角线元素为一元高斯分布的参数\(\sigma_j^2\)时，两个模型相同；多元模型能捕捉变量之间的关系，但是它要求\(m > n\)，且为了保证协方差矩阵可逆，不能有冗余特征。