机器学习之逻辑回归(Logistic Regression)
1. Classification
这篇文章我们来讨论分类问题(classification problems),也就是说你想预测的变量 y 是一个离散的值。我们会使用逻辑回归算法来解决分类问题。
之前的文章中,我们讨论的垃圾邮件分类实际上就是一个分类问题。类似的例子还有很多,例如一个在线交易网站判断一次交易是否带有欺诈性(有些人可以使用偷来的信用卡,你懂的)。再如,之前判断一个肿瘤是良性的还是恶性的,也是一个分类问题。
在以上的这些例子中,我们想预测的是一个二值的变量,或者为0,或者为1;或者是一封垃圾邮件,或者不是;或者是带有欺诈性的交易,或者不是;或者是一个恶性肿瘤,或者不是。
我们可以将因变量(dependant variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class)。可以使用0来代表负向类,1来代表正向类。
现在,我们的分类问题仅仅局限在两类上:0或者1。之后我们会讨论多分类问题,也就是说,变量 y 可以取多个值,例如0,1,2,3。
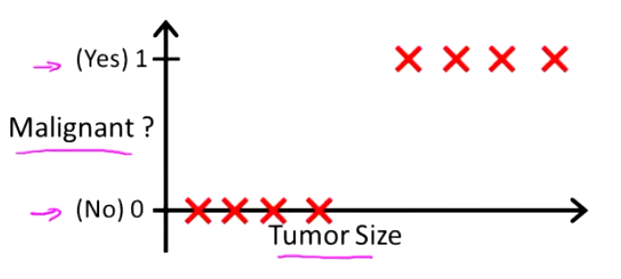
那么,我们如何来解决一个分类问题呢?来看以下例子:
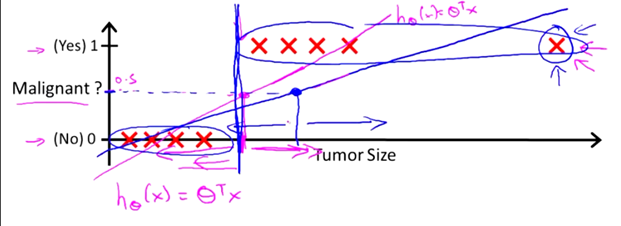
现在有这样一个分类任务,需要根据肿瘤大小来判断肿瘤的良性与否。训练集如上图所示,横轴代表肿瘤大小,纵轴表示肿瘤的良性与否,注意,纵轴只有两个取值,1(代表恶性肿瘤)和0(代表良性肿瘤)。
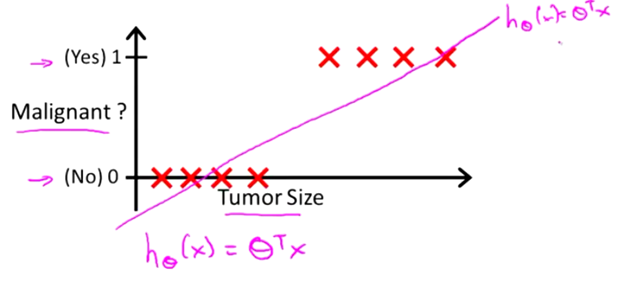
通过之前的博文,我们已经知道对于以上数据集使用线性回归来处理,实际上就是用一条直线去拟合这些数据。因此,你得到的 Hypothesis 可能如下:
那么,如果你想做出预测,一种可行的方式是如下:
从以上这个例子来看,似乎线性回归也能很好的解决分类问题。现在,我们对以上问题稍作一些改动。
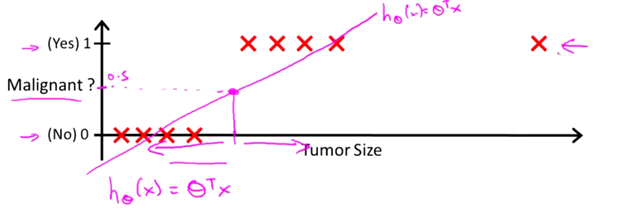
将横轴向右扩展,并且增加一个训练样本,如下:
此时,我们使用线性回归,会得到一条新的直线:
此时,我们再用0.5作为阈值来预测肿瘤的良性与否,就不合适了。
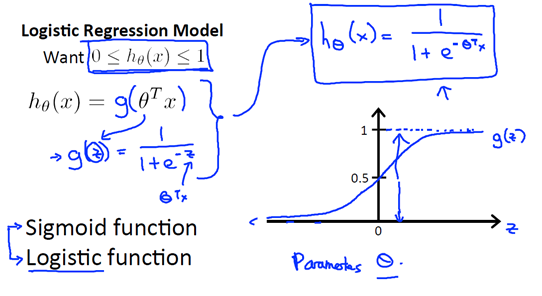
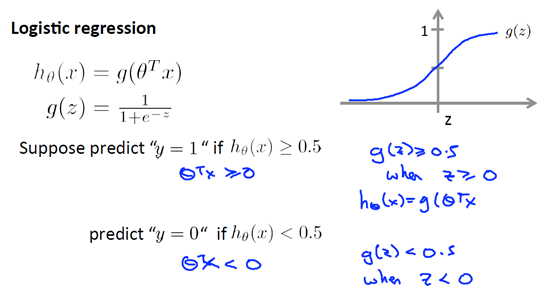
2. Hypothesis Representation
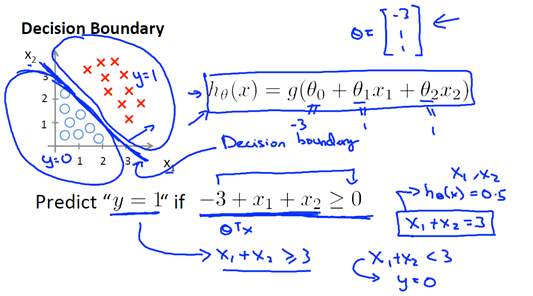
3. Decision boundary
强调一下,决策边界不是训练集的属性,而是假设本身及其参数的属性。只要我们给定了参数向量θ,决策边界就确定了。我们不是用训练集来定义的决策边界,我们用训练集来拟合参数θ,以后我们将谈论如何做到这一点。但是,一旦你有参数θ它就确定了决策边界。
4. Cost function
1
现在我们来讨论如何拟合逻辑回归中模型的参数θ。
具体来说,我们需要定义optimization objective 或者 cost function 来拟合参数θ,这便是监督学习问题中的逻辑回归模型的拟合问题。
如上图所示,我们有一个训练集,里面有m个训练样本,同之前一样,我们的每个样本使用n+1维的特征向量表示(x0 = 1)。并且由于是分类问题,我们训练集中的所有y,取值不是0就是1。假设函数的参数即为θ。那么,对于这个给定的训练集,我们如何拟合参数θ(或者说是选择参数θ)?
之前,我们使用线性回归模型来拟合假说参数θ时,使用了如下的代价函数,我们稍作改变,将原先的1/2m中的原先的1/2放到了求和符号里面去了。
现在我们使用另一种方式,来书写代价函数:
现在,我们能更清楚的看到代价函数是这个Cost函数(代价项)在训练集范围上的求和,再求均值(乘以1/m)。
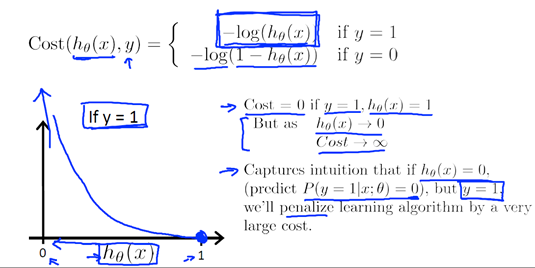
我们稍微简化一下这个式子,去掉这些上标会显得方便一些,所以Cost函数直接定义为:
对这个代价项(Cost函数)的理解是这样的:y我所期望的值,通过学习算法如果想要达到这个值,那么假设h(x)所需要付出的代价即为这个代价项。这个希望的预测值是h(x),而实际值则是y,干脆,全部去掉那些上标好了。
显然,在线性回归中,代价项(Cost函数)会被定义为:1/2乘以预测值h和实际值观测的结果y的差的平方。这个代价值可以很好地用在线性回归里
,但是对于逻辑回归却是不合适的。
2
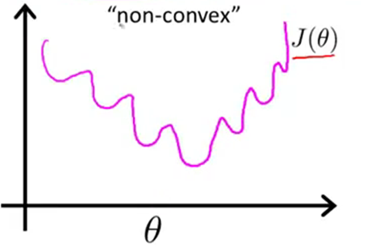
如果我们可以最小化代价函数J(θ)中的代价项(Cost函数),那么我们的确可以使用该代价项。但实际上,如果我们使用该代价项,那么代价函数J(θ)会变成关于参数θ的非凸函数。Why?
对于逻辑回归来说,这里的h函数是非线性的:
是一个很复杂的非线性函数,因此如果用h函数来构造我们在线性回归中所使用的代价项(Cost函数),接着再用该代价项来构造代价函数J(θ)。
那么J(θ)可能是一个这样的函数,有很多局部最优值:
不难发现,如果你把梯度下降法用在一个这样的函数上的话,我们并不能保证它会收敛到全局最小值。
显然,我们希望我们的代价函数J(θ)是一个凸函数,也就是一个单弓形函数,如下图所示:
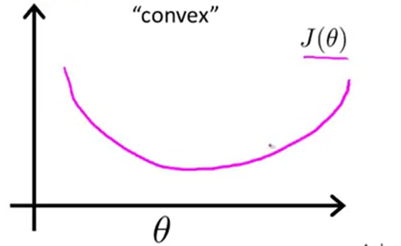
如果对它使用梯度下降法,那么我们可以保证梯度下降法会收敛到该函数的全局最小值。
因此我们在逻辑回归中使用这个代价项(Cost函数)的问题在于非线性的sigmoid函数的出现导致J(θ)成为一个非凸函数。
3
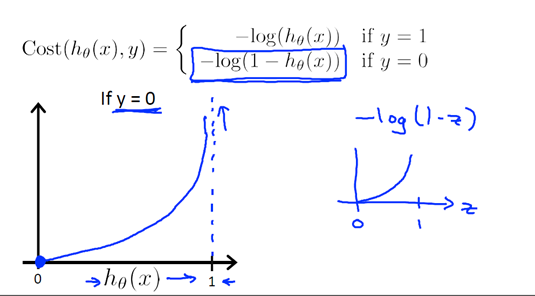
我们需要做的是,另外找一个本身是凸函数的代价项(Cost函数),可以让我们使用类似于梯度下降的算法来找到一个全局最小值。以下就是一个我们将要在逻辑回归中使用的代价项(Cost函数):
5. Simplified cost function and gradient descent
注意,此时θ是变量。我们的目标就是找出使J(θ)最小的θ值。








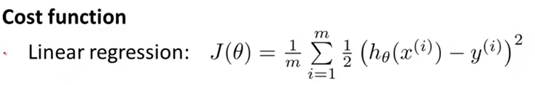
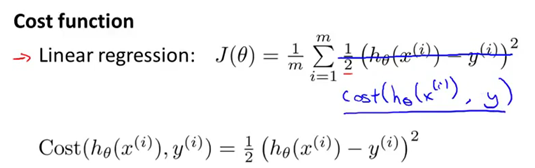
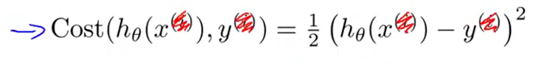
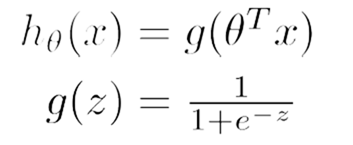
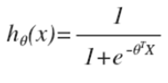
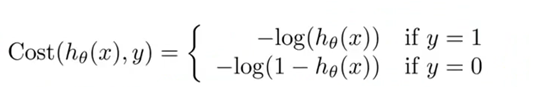






 浙公网安备 33010602011771号
浙公网安备 33010602011771号