[Scikit-learn] Dynamic Bayesian Network - Conditional Random Field
李航,第十一章,条件随机场
携代码:用 Python 通过马尔可夫随机场(MRF)与 Ising Model 进行二值图降噪【推荐!】
CRF:http://www.jianshu.com/p/55755fc649b1
概率无向图模型【基本性质】

团与最大团【基本性质】
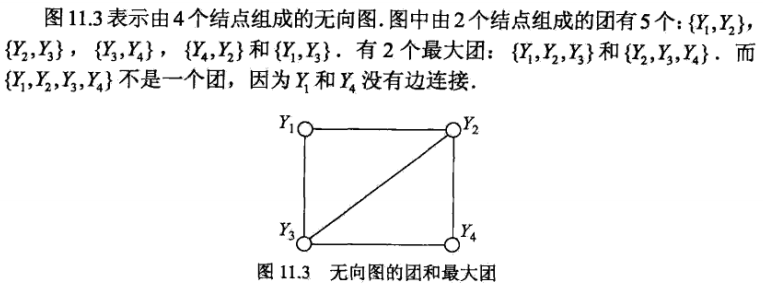
模型
------
首先什么是随机场呢,一组随机变量,他们样本空间一样,那么就是随机场。当这些随机变量之间有依赖关系的时候,对我们来说才是有意义的。
我们利用这些随机变量之间的关系建模实际问题中的相关关系,实际问题中我们可能只知道这两个变量之间有相关关系,但并不知道具体是多少,我们想知道这些依赖关系具体是什么样的,于是就把相关关系图画出来,然后通过实际数据训练去把具体的相关关系训练出来嵌入到图里,然后用得到的这个图去进行预测、去进行reference等很多事情。
马尔科夫随机场
那么为了简化某些为问题来说,也为了这个图画出来能用,我们会在画图的时候要遵循一些假设和规则,比如马尔科夫独立性假设。按照这个假设和规则来画图,画出来的图会满足一系列方便的性质便于使用。
马尔可夫独立性假设是说:对一个节点,在给定他所连接的所有节点的前提下,他与外接是独立的。就是说如果你观测到了这个节点直接连接的那些节点的值的话,那他跟那些不直接连接他的点就是独立的。形式上,我们是想把他设计成这个样子的,边可以传递信息,点与点之间通过边相互影响,如果观测到一个节点的取值或者这个节点的取值是常量,那么别的节点就无法通过这个节点来影响其他节点。所以对一个节点来说,如果用来连接外界的所有节点都被锁住了,那他跟外界就无法传递信息,就独立了。这比贝叶斯网络就直观多了,贝叶斯网络要判断两点之间独立还要看有没有v-structure,还要看边的指向。
呐,满足马尔可夫独立性的随机场,就叫马尔可夫随机场。它不仅具有我刚才说的那些性质,除此之外,还等价于吉布斯分布。
这些边具体是如何建模的呢,以什么形式记录这些概率信息的?贝叶斯网络每一条边是一个条件概率分布,P(X|Y),条件是父节点、结果是子节点。他有一个问题,就是当我知道A、B、C三个变量之间有相关关系,但是不知道具体是谁依赖谁,或者我不想先假设谁依赖谁,这个时候贝叶斯就画不出来图了。因为贝叶斯网络是通过变量之间的条件分布来建模整个网络的,相关关系是通过依赖关系(条件分布)来表达的。而马尔可夫随机场是这样,我不想知道这三个变量间到底是谁依赖谁、谁是条件谁是结果,我只想用联合分布直接表达这三个变量之间的关系。比如说两个变量A、B,这两个变量的联合分布是:
| A, B | P(A, B) |
|--------------+---------|
| A = 0, B = 0 | 100 |
| A = 0, B = 1 | 10 |
| A = 1, B = 0 | 20 |
| A = 1, B = 1 | 200 |
【这里与有向图不一样的地方是,P(a,b)不再是用概率表示,但这并不会带来什么影响】
这个分布表示,这条边的功能是使它连接的两点(A和B)趋同,当A = 0的时候B更可能等于0不太可能等于1,当A = 1的时候B更可能等于1不太可能等于0。这样一来你知道了三个变量之间的联合分布,那他们两两之间的条件分布自然而然就在里面。
这样出来的图是等价于吉布斯分布的,就是说,你可以只在每个最大子团上定义一个联合分布(而不需要对每个边定义一个联合分布),整个图的联合概率分布就是这些最大子团的联合概率分布的乘积。当然这里最大子团的联合概率并不是标准的联合概率形式,是没归一化的联合概率,叫factor(因子),整个图的联合概率乘完之后下面再除一个归一化因子和就归一化了,最终是一个联合概率,每个子团记载的都是因子,是没归一化的概率,严格大于零,可以大于一。但关键是依赖关系、这些相关关系已经encode在里面了。
条件随机场
条件随机场是指这个图里面一些点我已经观测到了,求,在我观测到这些点的前提下,整张图的分布是怎样的。就是given观测点,你去map inference也好你去做之类的事情,你可能不求具体的分布式什么。这里还要注意的是,马尔科夫随机场跟贝叶斯网络一样都是产生式模型,条件随机场才是判别式模型。
这是条件随机场,NER(命名实体识别)这个任务用到的是线性链条件随机场。
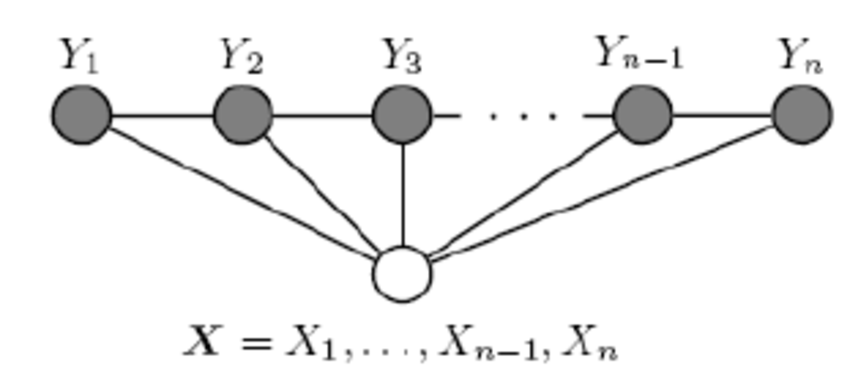
线性链条件随机场的形式是这样的,观测点是你要标注的这些词本身和他们对应的特征,例如说词性是不是专有名词、语义角色是不是主语之类的。隐节点,是这些词的标签,比如说是不是人名结尾,是不是地名的开头这样。这些隐节点(就是这些标签),依次排开,相邻的节点中间有条边,跨节点没有边(线性链、二阶)。然后所有观测节点(特征)同时作用于所有这些隐节点(标签)。至于观测节点之间有没有依赖关系,这些已经不重要了,因为他们已经被观测到了,是固定的。
这是线性链条件随机场的形式。
呐,这些特征是怎么表达的呢?是这样,他有两种特征:
-
- 一种是转移特征,就是涉及到两个状态之间的特征。
- 另一种就是简单的状态特征,就是只涉及到当前状态的特征。
特征表达形式比较简单,就是你是否满足我特征所说的这个配置,是就是1,不是就是0。比如说,上一个状态是地名的中间,且当前词是'国'(假设他把中国分词 拆成两个了),且当前词的词性是专有名词、且上一个词的词性也是专有名词,如果满足这个配置、输出就是1、不满足就输出0。然后这些特征每个都有一个权重,我们最后要学的就是这些权重。特征跟权重乘起来再求和,外面在套个exp,出来就是这个factor的形式。这是一个典型的对数线性模型的表达方式。这种表达方式非常常见,有很多好处,比如为什么要套一个exp呢?
-
- 一方面,要保证每一个factor是正的,factor可以大于一也可以不归一化,但一定要是正的。
- 另一方面,我们最后要通过最大似然函数优化的,似然值是这些 factor的累乘,对每一个最大子团累乘。这么多项相乘没有人直接去优化的,都是取log变成对数似然,然后这些累乘变成累加了嘛,然后优化这个累加。无论是算梯度用梯度下降,还是另导数为零求解析解都很方便了(这个表达形态下的目标函数是凸的)。你套上exp之后,再取对数,那么每个因子就变成一堆特征乘权重的累积,然后整个对数似然就是三级累积,对每个样本、每个团、每个特征累积。这个形式就很有利了,你是求导还是求梯度还是怎样,你面对的就是一堆项的和,每个和是一个1或者一个0乘以一个 权重。
- 当然后面还要减一个log(Z),不过对于map inference来说,给定Z之后log(Z)是常量,优化可以不带这一项。
推断
------
线性链的条件随机场跟线性链的隐马尔科夫模型一样,一般推断用的都是维特比算法。这个算法是一个最简单的动态规划。
首先我们推断的目标是给定一个X,找到使P(Y|X)最大的那个Y嘛。然后这个Z(X),一个X就对应一个Z,所以X固定的话这个项是常量,优化跟他没关系(Y的取值不影响Z)。然后 exp也是单调递增的,也不带他,直接优化exp里面。所以最后优化目标就变成了里面那个线性和的形式,就是对每个位置的每个特征加权求和。比如说两个状态的话,它对应的概率就是从开始转移到第一个状态的概率加上从第一个转移到第二个状态的概率,这里概率是只exp里面的加权和。那么这种关系下就可以用维特比了,首先你算出第一个状态取每个标签的概率,然后你再计算到第二个状态取每个标签得概率的最大值,这个最大值是指从状态一哪个标签转移到这个标签的概率最大,值是多 少,并且记住这个转移(也就是上一个标签是啥)。然后你再计算第三个取哪个标签概率最大,取最大的话上一个标签应该是哪个。以此类推。整条链计算完之后, 你就知道最后一个词去哪个标签最可能,以及去这个标签的话上一个状态的标签是什么、取上一个标签的话上上个状态的标签是什么,酱。这里我说的概率都是 exp里面的加权和,因为两个概率相乘其实就对应着两个加权和相加,其他部分都没有变。
学习
------
这是一个典型的无条件优化问题,基本上所有我知道的优化方法都是优化似然函数。典型的就是梯度下降及其升级版(牛顿、拟牛顿、BFGS、L-BFGS),这里版本最高的就是L-BFGS了吧,所以一般都用L-BFGS。除此之外EM算法也可以优化这个问题。

马尔科夫随机场 - 去噪

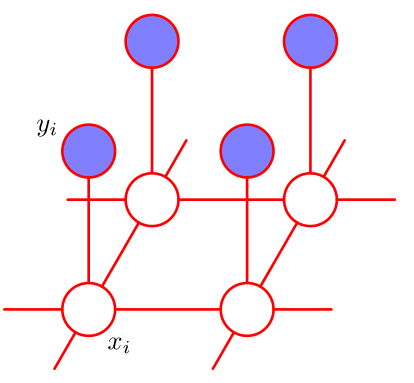
【有点难理解的东西,还是直接实战的好】
数学表示:
-
- yi:噪声图中的像素
- xi:原图中的像素,对应噪声图中的 yi
既然噪声图是从原图添加噪声而来,我们拥有了先验知识 1:
yi和xi有很强的联系。
一般图片里,每个像素和与它相邻的像素值应当较为接近,比如上图中的黑色笔画和白色负空间,除了边缘以外,黑色的像素周围都是黑色像素,白色像素的周围都是白色像素(连成一片))。这样我们就得到了先验知识 2:
xi和与它相邻的其他像素也存在较强的联系
如果我们狠一点,假设原图像素只与它的直接相邻像素有联系(即具备条件独立性质),我们就可以得到一个具备局部马尔可夫性质(Local Markov property)的图模型
如此,找”最大团“也相对简单,都是成对的结点。在这样一个图模型里,我们有两种团(clique):
- {xi, yi},即原图像素与噪声图像素对
- {xi, xj},其中 xj 表示与 xi 相邻的像素
这两种团合并起来,得到的 {xi, yi, xj} 显然是一个最大团(Maximal Clique),此时我们可以利用它来对这个马尔可夫随机场进行 factorization,即求得其联合概率分布关于最大团 xC = {xi, yi, xj} 的函数。
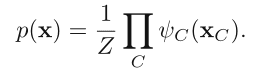
【这里又最大团又变成了三个结点构成】
其中 Z 为 partition function,是 p(x) 的归一化常数(normalization constant),求法参见 PRML 8.3.2。因为与我们的实现不相关,这里不赘述。
ψC(xC) 即所谓的 potential function,为了方便我们通常只求它的对数形式 E(xC)(按照其物理意义称为 energy function)
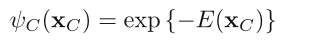
关于 factorization 的过程和推导可以参见 PRML 8.3.2,这里我们需要做的是定义一个 energy function:
-
- 在降噪的过程中 energy 越低,
- 联合概率 P(X=x) 就越大,
- 降噪过的图像与原图会越一致
Step 1. 因为我们需要处理的是二值图,首先我们定义 xi ∈ {-1, +1},假设这里白色为1,黑色为-1。
对于原图像素与噪声图像素构成的团 {xi, yi},我们定义一项 −ηxiyi,其中 η 为一个非负的权重。当两者同号时【1*1 or (-1)*(-1),表示噪声图像素与原图像素较为接近时】,这项的值为−η,异号时为 η。这一项能够降低 energy(因为为负)。
Step 2. 对于噪声图中相邻像素构成的团 {xi, xj},我们定义一项 −βxixj,其中 β 为一个非负的权重。这样,当处理过的图像里相邻的像素较为接近时,这一项能够降低 energy(因为为负)。
Step 3. 最后,我们再定义一项 hxi,使处理过的图像整体偏向某一个像素值。
对图像中的每一个像素,将这三项加起来,就得到我们的 energy function:
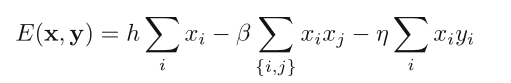
对应联合概率:
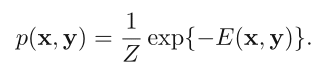
显然 energy 越低,降噪过的图像与原图一致的概率越高。
(注意因为我们这里求的 E 已经对整个矩阵求和,即对应 potential function 的积,所以计算联合概率分布的时候不需要再求积)
代码分析:
使用 Python 实现这个 energy function 时,我们可以使用一个 closure 来实现一个 function factory,通过传递beta(β),eta(η)和 h 参数,生成对应的 energy function。
此外为了方便,我们假设传入的x和y不是一维向量,而是对应图像的二维矩阵(注意是np.ndarray而不是nd.matrix,前者的*才是array multiplication即逐个元素相乘,后者的*是矩阵乘法)。
import numpy as np
def E_generator(beta, eta, h):
"""Generate energy function E.
Usage: E = E_generator(beta, eta, h)
Formula:
E = h * \sum{x_i} - beta * \sum{x_i x_j} - eta * \sum{x_i y_i}
"""
def E(x, y):
"""Calculate energy for matrices x, y.
Note: the computation is not localized, so this is quite expensive.
"""
# sum of products of neighboring paris {xi, xj},参考“技巧解释”
# 因为边界元素不一定有四个邻居,−βxixj这项存在边界问题,我们需要特别处理,
# 利用 numpy 的 fancy index,写起来并不困难,如下。
xxm = np.zeros_like(x)
xxm[ :-1,: ] = x[1: , : ] # down
xxm[1:, : ] += x[ :-1, : ] # up
xxm[ :, :-1] += x[ : ,1: ] # right
xxm[ :, 1: ] += x[ : , :-1] # left
xx = np.sum(xxm * x)
xy = np.sum(x * y)
xsum = np.sum(x)
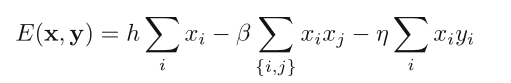 return h * xsum - beta * xx - eta * xy
return E
return h * xsum - beta * xx - eta * xy
return E
技巧:注意到如果用 xi0 ~ xi3 表示 xi 的四个邻居,则 xi * xi0 + xi * xi1 + xi * xi2 + xi * xi3 = + xi * (xi1 + ... + xi3),即乘法结合律,因此我们可以先将邻居相加,再与 x相乘。
注意这里生成的E每次都要对矩阵中的所有元素进行运算,所以即使有 numpy 加持,开销依然较大。后面我们会按照需求进行优化。
基本思想:
注意如果我们固定 y 作为先验知识(假设噪声图不变),我们所求的概率就变成了 p(x|y),这种模型叫做 Ising Model,【这不就成了CRF了么?】
在统计物理中有广泛的应用。这样我们的问题就成了以 y 为基准,想办法不断变动 x,然后找出最接近原图的 x。
Iterated Conditional Modes
一种最简单的办法是:(ICM)
- 先将 x 初始化为 y,
- 然后遍历每一个元素,对每个元素分别尝试 1 和 -1 两种状态,
- 选择能够得到更低的 energy 的那个,实际上相当于一种贪心的策略。
这种方法称为 Iterated Conditional Modes(ICM),由 Julian Besag 在 1986 年的论文 On the Statistical Analysis of Dirty Pictures 中提出(这篇论文在 80 年代英国数学家所著论文里引用数排名第一……)。
因为 ICM 的每一步实际上固定住了其他元素,只变动当前遍历到的那个元素,所以我们可以将 E的计算 localize,只对受影响的那一小片区域重新计算。
我们可以让 function factory E_generator 返回两个版本的 E:
-
- 一个是全局的,用于第一次计算 E,
- 一个是局部的,用于计算某个元素两种状态下的 E。
这里添加了两个函数:
def E_generator(beta, eta, h):
def E(x, y):
... # as shown before
def is_valid(i, j, shape):
"""Check if coordinate i, j is valid in shape."""
return i >= 0 and j >= 0 and i < shape[0] and j < shape[1]
def localized_E(E1, i, j, x, y):
"""Localized version of Energy function E.
Usage: old_x_ij, new_x_ij, E1, E2 = localized_E(Ecur, i, j, x, y)
"""
oldval = x[i, j]
newval = oldval * -1 # flip
# local computations
E2 = E1 - (h * oldval) + (h * newval)
E2 = E2 + (eta * y[i, j] * oldval) - (eta * y[i, j] * newval)
adjacent = [(0, 1), (0, -1), (1, 0), (-1, 0)]
neighbors = [x[i + di, j + dj] for di, dj in adjacent
if is_valid(i + di, j + dj, x.shape)]
E2 = E2 + beta * sum(a * oldval for a in neighbors)
E2 = E2 - beta * sum(a * newval for a in neighbors)
return oldval, newval, E1, E2
return E, localized_E
ICM实现:
def ICM(y, E, localized_E):
"""Greedy version of simulated_annealing()."""
x = np.array(y)
Ebest = Ecur = E(x, y) # initial energy
initial_time = time.time()
energy_record = [[0.0, ], [Ebest, ]]
accept, reject = 0, 0
for idx in np.ndindex(y.shape): # for each pixel in the matrix
old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y)
if (E2 < Ebest):
Ecur, x[idx] = E2, new
Ebest = E2 # update Ebest
else:
Ecur, x[idx] = E1, old
# record time and Ebest of this iteration
end_time = time.time()
energy_record[0].append(end_time - initial_time)
energy_record[1].append(Ebest)
return x, energy_record

可以看到大约 96% 的像素与原图一致。不过光从视觉上看,降噪过后的图依然有不少明显的噪点,这是因为 ICM 采取的类似贪心的策略使得它容易陷入局部最优(local optimum)。
如果想要得到一个更好的降噪结果,我们显然要采取一种能够得到全局最优(global optimum)的策略。
故,可以使用模拟退火的办法。
模拟退火
其实这个问题可以看成一个搜索问题:
“在所有 x 的两种状态组成的状态空间里(假设有 n 个像素,那么状态空间大小为 2n),找到能使 energy 最低的状态。“
由于状态空间大小呈指数级增长,仅仅是对于一个有 240 × 180 = 43,200 个像素的图片来说,这个状态空间就已经不可能使用暴力搜索解决了(实际上是 NP-Hard 的),所以我们需要考虑其他的搜索策略。
这里我们可以尝试使用模拟退火(Simulated annealing),在有限的时间内找到尽可能好的解。本方法由 Stuart Geman 与 Donald Geman (兄弟哟) 在 1984 年的论文 Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images 中提出,并且文中对模拟退火可收敛至全局最优进行了详细的证明(这篇论文和之前 Julian Besag 的那篇都是 ISI Highly Cited Paper,引用数相当魔性……)。
模拟退火需要一个控制温度的 schedule,具体怎样可以自己调,只需要在迭代次数 k 接近最大迭代次数 kmax 时逼近 0 即可,这里设定为:
def temperature(k, kmax):
"""Schedule the temperature for simulated annealing."""
return 1.0 / 500 * (1.0 / k - 1.0 / kmax)
模拟退火的核心在于:当局部变化导致状况恶化(这里为能量变大)时,依据当前温度 t,设该变化对“全局最优”有利的概率为 e△E/t,按照这个概率来确定是否保留这个变化,即所谓的 transition probabilities,如下
def prob(E1, E2, t):
"""Probability transition function for simulated annealing."""
return 1 if E1 > E2 else np.exp((E1 - E2) / t)
模拟退火实现:
def simulated_annealing(y, kmax, E, localized_E, temp_dir):
"""Simulated annealing process for image denoising.
Parameters
----------
y: array_like
The noisy binary image matrix ranging in {-1, 1}.
kmax: int
The maximun number of iterations.
E: function
Energy function.
localized_E: function
Localized version of E.
temp_dir: path
Directory to save temporary results.
Returns
----------
x: array_like
The denoised binary image matrix ranging in {-1, 1}.
energy_record:
[time, Ebest] records for plotting.
"""
x = np.array(y)
Ebest = Ecur = E(x, y) # initial energy
initial_time = time.time()
energy_record = [[0.0, ], [Ebest, ]]
for k in range(1, kmax + 1): # iterate kmax times
start_time = time.time()
t = temperature(k, kmax + 1)
print "k = %d, Temperature = %.4e" % (k, t)
accept, reject = 0, 0 # record the acceptance of alteration
for idx in np.ndindex(y.shape): # for each pixel in the matrix
old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y)
p, q = prob(E1, E2, t), random()
if p > q:
accept += 1
Ecur, x[idx] = E2, new
if (E2 < Ebest):
Ebest = E2 # update Ebest
else:
reject += 1
Ecur, x[idx] = E1, old
# record time and Ebest of this iteration
end_time = time.time()
energy_record[0].append(end_time - initial_time)
energy_record[1].append(Ebest)
print "k = %d, accept = %d, reject = %d" % (k, accept, reject)
print "k = %d, %.1f seconds" % (k, end_time - start_time)
# save temporary results
temp = sign(x, {-1: 0, 1: 255})
temp_path = os.path.join(temp_dir, 'temp-%d.png' % (k))
Image.fromarray(temp).convert('1', dither=Image.NONE).save(temp_path)
print "[Saved]", temp_path
return x, energy_record
Result:

无论是 ICM 还是模拟退火,都是通过最小化能量来找到原图的近似。
后来 Greig, Porteous 和 Seheult 提出了使用 graph cuts 的模型,将能量值的最小化转化为最大化解的后验估计(a posteriori estimate),进而转为计算机科学里常见的 max-flow/min-cut 的问题,求解后能够得到更好的效果
(参考 D.M. Greig, B.T. Porteous and A.H. Seheult (1989), Exact maximum a posteriori estimation for binary images, Journal of the Royal Statistical Society Series B, 51, 271–279.)。
条件随机场 - 词性标注 based on linear chain CRF
From: http://blog.echen.me/2012/01/03/introduction-to-conditional-random-fields/
举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!
给一个句子中的每个单词注明词性。比如这句话:“Bob drank coffee at Starbucks”,注明每个单词的词性后是这样的:“Bob (名词) drank(动词) coffee(名词) at(介词) Starbucks(名词)”。
下面,就用条件随机场来解决这个问题。
以上面的话为例,有5个单词,我们将:(名词,动词,名词,介词,名词)作为一个标注序列,称为l,可选的标注序列有很多种,我们要在这么多的可选标注序列中,挑选出一个最靠谱的作为我们对这句话的标注。
假如我们给每一个标注序列打分,打分越高代表这个标注序列越靠谱,我们至少可以说,凡是标注中出现了动词后面还是动词的标注序列,要给它负分!!
特征函数
上面所说的动词后面还是动词就是一个特征函数,我们可以定义一个特征函数集合,用这个特征函数集合来为一个标注序列打分,并据此选出最靠谱的标注序列。
也就是说,每一个特征函数都可以用来为一个标注序列评分,把集合中所有特征函数对同一个标注序列的评分综合起来,就是这个标注序列最终的评分值。
特征函数,就是这样的函数,它接受四个参数:【输入】
-
- 句子s(就是我们要标注词性的句子)
- i,用来表示句子s中第i个单词
- l_i,表示要评分的标注序列给第i个单词标注的词性
- l_i-1,表示要评分的标注序列给第i-1个单词标注的词性
输出值是0或者1:【输出】
-
- 0表示要评分的标注序列不符合这个特征,
- 1表示要评分的标注序列符合这个特征。
特征函数 to 概率
定义好一组特征函数后,我们要给每个特征函数fj赋予一个权重λj。现在,只要有一个句子s,有一个标注序列l,我们就可以利用前面定义的特征函数集来对l评分。
m: 特征函数集中的个数
n: 句子单词个数
对这个分数进行指数化和标准化,我们就可以得到标注序列l的概率值p(l|s),如下所示:
-
- 逻辑回归是用于分类的对数线性模型,
- 条件随机场是用于序列化标注的对数线性模型。
当l_i是“副词”并且第i个单词以“ly”结尾时,我们就让f1 = 1,其他情况f1为0。不难想到,f1特征函数的权重λ1应当是正的。而且λ1越大,表示我们越倾向于采用那些把以“ly”结尾的单词标注为“副词”的标注序列。
如果i=1,l_i=动词,并且句子s是以“?”结尾时,f2=1,其他情况f2=0。同样,λ2应当是正的,并且λ2越大,表示我们越倾向于采用那些把问句的第一个单词标注为“动词”的标注序列。
当l_i-1是介词,l_i是名词时,f3 = 1,其他情况f3=0。λ3也应当是正的,并且λ3越大,说明我们越认为介词后面应当跟一个名词。
一个条件随机场就这样建立起来了,让我们总结一下:
为了建一个条件随机场,我们首先要定义一个特征函数集,每个特征函数都以整个句子s,当前位置i,位置i和i-1的标签为输入。
然后为每一个特征函数赋予一个权重,然后针对每一个标注序列l,对所有的特征函数加权求和,必要的话,可以把求和的值转化为一个概率值。
HMM和CRF的关系:
每一个HMM模型都等价于某个CRF
但是,CRF要比HMM更加强大,原因主要有两点:
-
-
CRF可以定义数量更多,种类更丰富的特征函数。HMM模型具有天然具有局部性,就是说,在HMM模型中,当前的单词只依赖于当前的标签,当前的标签只依赖于前一个标签。这样的局部性限制了HMM只能定义相应类型的特征函数,我们在上面也看到了。但是CRF却可以着眼于整个句子s定义更具有全局性的特征函数,如这个特征函数:
如果i=1,l_i=动词,并且句子s是以“?”结尾时,f2=1,其他情况f2=0。
-
CRF可以使用任意的权重 将对数HMM模型看做CRF时,特征函数的权重由于是log形式的概率,所以都是小于等于0的,而且概率还要满足相应的限制,如
-
但在CRF中,每个特征函数的权重可以是任意值,没有这些限制。


