HOJ 1402 整数划分

HOJ1402 整数划分

http://acm.hit.edu.cn/hoj/problem/view?id=1402

【题目描述】

整数划分是一个经典的问题。希望这道题会对你的组合数学的解题能力有所帮助。

Input

每组输入是两个整数n和k。(1 <= n <= 50, 1 <= k <= n)

Output

对于每组输入，请输出六行。

第一行： 将n划分成若干正整数之和的划分数。
第二行： 将n划分成k个正整数之和的划分数。
第三行： 将n划分成最大数不超过k的划分数。
第四行： 将n划分成若干奇正整数之和的划分数。
第五行： 将n划分成若干不同整数之和的划分数。
第六行： 打印一个空行。

Sample Input

5 2

Sample Output

7
2
3
3
3

Hint:

1. 将5划分成若干正整数之和的划分为： 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1
2. 将5划分成2个正整数之和的划分为： 3+2, 4+1
3. 将5划分成最大数不超过2的划分为： 1+1+1+1+1, 1+1+1+2, 1+2+2
4. 将5划分成若干奇正整数之和的划分为： 5, 1+1+3, 1+1+1+1+1
5. 将5划分成若干不同整数之和的划分为： 5, 1+4, 2+3

 

【算法分析】

　　

本题相当于5个小问题，首先来看最容易做的第5个小问题：将n划分成若干不同整数之和的划分数。则是一个典型的背包装物品问题，把问题转化一下，即一个容量为n的背包，重量分别为1到n的物品各一个，求用若干物品将背包填满的方案总数。

利用动态规划的思想，很容易得到方程F[I,J] = F[I-1,J] +F[I-1,J-I]，其中F[I,J]表示从前I个物品中用若干个组成的总重量为J的方案总数，转移时要保证F[I-1,J-I]有意义。答案为F[n,n]，时间复杂度为O(n²)。

对于前3个小问题可以归结为一个问题，即第2个小问题：把将n划分成k个正整数之和的划分数。

为了避免重复，我们需要按照不下降的顺序进行排列。我们形象地可以把n的k份自然数划分看作n块积木堆成k列，那么不妨设这n块积木从左到右被堆成“阶梯状”。比如，下图表示的是3种10的4份自然数划分。

 

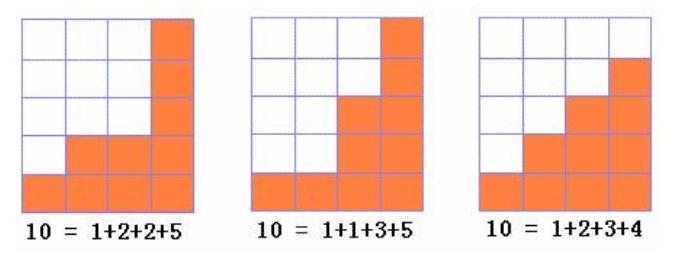
而将该图旋转90度，可以很容易想出一种状态表示方法。

 

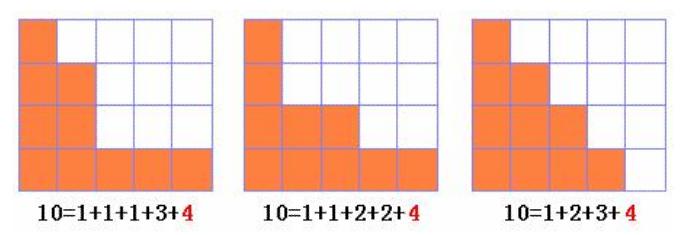
设F[I,J,K]表示把J划分成I份最大为K的划分方案数，则有F[I,J,K] = ∑F[I-1,J-K,L]，其中L = 1..K。时间复杂度为O（n²k²）。

而如果观察第一个图，我们还可以得到一种状态表示方式。设F[I,J]表示把I划分成J份的划分方案数，则有F[I,J] = ∑F[I-J,K] ，其中K = 0..J。时间复杂度为O（nk²）。

又由于F[I,J]=∑F[I-J,K]（K = 0..J）=∑F[I-J,K]（K = 0..J-1）+F[I-J,J] = F[I-1,J-1]+F[I-J,J]，这样就把时间复杂度降为O（nk）。从另外一个角度想，我们在第一个图中“截去底边”，由于存在一个划分方案中含1的情况，我们无法确定在“截去底边”之后要把I-J分为几个数，那么不妨将划分方案中含1的情况单独列出来讨论，直接得到F[I,J] = F[I-1,J-1]+F[I-J,J]。

对于第1个小问题的答案是∑F[N,I]（I = 1..N），第2个小问题的答案显然是F[N,K]，而第3个小问题的答案则是∑F[N,I]（I = 1..K），考虑上面旋转90度之后的图，你会发现，F[N,I]集合中的最高高度均为I，即将n划分成最大数为I的方案数。

最后来看第4个小问题，就是第2个小问题的分奇偶版本，那么设F[I,J]表示把I划分成J个奇数的划分方案数，G[I,J] 表示把I划分成J个偶数的划分方案数。那么还是用“截去底边”的思想，显然有G[I,J] = F[I-J,J]。但F[I,J]却不是直接等于G[I-J,J]，因为这里又存在一个划分方案中含1的情况，同样将划分方案中含1的情况单独列出来讨论，则有F[I,J] = G[I-J,J] + F[I-1,J-1]。最后的答案就是∑F[N,I]（I = 1..N），时间复杂度为O(n²)。

 

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

const int maxn = 51;

int n,k;
int f[maxn][maxn], g[maxn][maxn];
int f1[maxn][maxn], f2[maxn][maxn];

int main () {
    int i, j;
    int ans1, ans2, ans3, ans4, ans5;
    f1[0][0] = 1;
    for (i = 1; i < maxn; i ++)
        for (j = 1; j <= i; j ++)
            f1[i][j]=f1[i-j][j]+f1[i-1][j-1];
    f[0][0] = g[0][0] = 1;
    for (i = 1; i < maxn; i ++)
        for (j = 1; j <= i; j ++){
            g[i][j] = f[i - j][j];
            f[i][j] = f[i - 1][j - 1] + g[i - j][j];
        }
    for (i = 0; i < maxn; i ++)
        f2[i][0] = 1;
    for (i = 1; i < maxn; i ++)
        for (j = 1; j < maxn; j ++){
            f2[i][j] = f2[i - 1][j];
            if (j - i >= 0)
                f2[i][j] += f2[i - 1][j - i];
        }

    while (scanf ("%d %d", &n, &k) != EOF){
        ans1 = ans2 = ans3 = ans4 = ans5 = 0;
        for (i = 1; i <= n; i ++)
            ans1 += f1[n][i];
        ans2 = f1[n][k];
        for (i = 1; i <= k; i ++)
            ans3 += f1[n][i];
        for (i = 1; i <= n; i ++)
            ans4 += f[n][i];
        ans5 = f2[n][n];
        printf ("%d\n%d\n%d\n%d\n%d\n\n", ans1, ans2, ans3, ans4, ans5);
    }
    return 0;
}