高效算法的常用技术(算法导论)

对于高效算法, 有些比较简单的技术, 如分治法, 随机化, 和递归求解技术.
这边介绍些更为复杂的技术, 动态规划, 贪心算法

当对于复杂问题设计算法时, 首先会想到使用分治法 来解决, 分而治之, 一个很有哲理性的思路, 再复杂的问题都可以不断分解到你可以轻松解决的粒度, 把所有简单问题都解决完后, 组合在一起就得到了复杂问题的解, 可以看出其中典型的递归求解的思路. 使用分治法的要求, 各个子问题是独立 的 (即不包含公共的子子问题,子问题不重叠 ).
如果子问题重叠, 用分治法就比较低效, 因为需要重复解决相同子问题, 这就产生算法冗余, 要考虑使用动态规划.

动态规划 的实质是分治思想 和解决冗余 ，因此动态规划是一种将问题实例分解为更小的、相似的子问题，并存储子问题的解而避免计算重复的子问题，以解决最优化问题的算法策略。因为要解决最优问题, 要产生一个全局最优解, 而这个最优解需要考虑所包含所有子问题的解, 你可以想象这个递归树, 每一层都需要考虑自其以下各层的子问题的解, 所以会产生大量的子问题重叠, 这种情况就需要动态规划.

同样时解决最优问题, 很多时候局部最优就可以代表全局最优(这是普通最优问题的一个特例), 这时再用动态规划也没有问题, 普通算法肯定可以使用于某一特例的, 但比较低效.
对于这种特例, 可以用贪心算法 , 贪心法的当前选择可能要依赖已经作出的所有选择，但不依赖于有待于做出的选择和子问题 。因此贪心法可以自顶向下 ，一步一步地作出贪心选择(局部最优), 最终解决全局最优问题.

而动态规划一定是自下而上 解决的, 因为它的最优解必须依赖于子问题的解, 所以必须先解子问题. 虽然你在编码的时候, 可以选择递归(Top-down 思路)或迭代(Bottom-up思路), 但最终执行的时候都是自下而上的.

动态规划

  动态规划用于子问题重叠的问题, 利用保存子问题的解来避免重复计算子问题, 从而大大提高算法的效率, 可以说动态规划就是一种拿空间换时间的优化算法.
适合采用动态规划的最优问题中两个要素, 最优子结构 和重叠子问题

对于动态规划而言, 最重要也是最难的一步就是找到最优子结构, 其他都很简单. 怎么找?
大白话就是, 把问题分为子问题, 并证明当假设能得到子问题的最优解时, 通过子问题最优解的组合或简单的选择就可以得到全局最优解.
算法导论上给出了寻找最优子结构的步骤, 个人认为那个步骤并不能真正帮助你容易的找到最优子问题.
这个其实只能意会不能言传, 找最优子问题是个艺术......

动态规划算法的运行时间 取决于两个因素的乘积, 子问题的总个数和每个子问题中有多少种选择

不明白就通过几个例子来看看怎么使用动态规划吧

一, 矩阵连乘问题
A*B*C*D*E*F*G 对于一个矩阵连乘问题, 乘的顺序会大大影响效率, 所以求最优顺序是很有价值的
最优子问题,
假设矩阵(1....n)连乘问题, 切分为子问题, (1...k), (k+1,n)(1<k<n)两个连乘子问题, 如果能知道他们的最优解, 是否可以知道全局最优解
当把k从1到n遍历一遍, 分别计算每种划分的耗费, 我们可以得到一个最优k值, 这就是全局最优解.

运行时间 , 子问题总数为n² , 每个子问题要面临n个选择, 比如上面的k, 所以运行时间在O(n³ )

在找到最优子问题后, 其他就很简单了, 对于第一个例子, 给出完整的过程
设矩阵连乘长度为n, 对于 1<=i 我们用m(i,j)来表示从第i个到第j个矩阵连乘的最小耗费
m(i,j) = min(m(i,k) + m(k+1,j) + 子矩阵相乘耗费) 其中i<=k
对于动态规划问题可以用bottom-up或top-down的思路来解决:
就矩阵连乘问题为例解释一下两个思路
Bottom-up思路:
算法导论中给出了这个算法.
Matrix_chain_order(p)
    建立两个辅助表
    m(i,j)用来记录从第i个矩阵到第j个矩阵乘的最小耗费
    s(i,j)记录那个能使耗费最小的k值
    n = length(p)-1
    for l ← 2 to n  l代表子链的长度, 比如p长为6, 那子链的长度从2到5
        do for i ← 1 to n - l + 1 遍历所有可能的子链, 比如p长为6, 子链长为5, 那可能的子链为1~5, 2~6               
            do j ← i + l - 1                找到子链的末尾
            m[i, j] ← ∞
            for k ← i to j - 1    尝试不同的k去划分这个矩阵乘问题,找到最优并保存
                do q ← m[i, k] + m[k + 1, j] + p_i-1 p_k p_j
                   if q < m[i, j]  
                      then m[i, j] ← q
                           s[i, j] ← k
     return m and s
这就是bottom-up思路, 从最小链长2起迭代计算, 并保存后面要反复用到的m(i,j)的值. 迭代到6后, 从s[i,j]里面取出各个最优的k, 就得到了最优解

Top-down 思路: 算法导论称这种思路为备忘录(memoization)
这个我自己写下.
建立全局m[i,j], s[i,j] 并清0
Matrix_chain(p,i,j)
    if m[i,j] >0 计算过了就不用重复计算
        return m[i,j]
    n = j-1
    m[i, j] ← ∞
    for k ← i to n 尝试不同的k取划分这个矩阵乘
        do q ← Matrix_chain(p,i, k) + Matrix_chain(p,k+1,j) + p_i-1 p_k p_j
           if q < m[i, j]  
              then m[i, j] ← q
                   s[i, j] ← k
    return m[i,j]         
这个就是自上而下的思路, 调用 Matrix_chain(p,1,length(p))即可.

二, 装配线调度问题

Colonel汽车公司在有两条装配线的工厂内生产汽车，一个汽车底盘在进入每一条装配线后，在每个装配站会在汽车底盘上安装不同的部件，最后完成 的汽车从装配线的末端离开。每一条装配线上有n个装配站，编号为j=1,2,...,n，将装配线i（i为1或2）的第j个装配站表示为S(i,j)。装 配线1的第j个站 S(1,j)和装配线2的第j个站S(2,j)执行相同的功能。然而这些装配站是在不同的时间建造的，并且采用了不同的技术，因此，每个站上完成装配所需 要的时间也不相同，即使是在两条装配线相同位置的装配站也是这样。把每个装配站上所需要的装配时间记为a(i,j)，并且，底盘进入装配线i需要的时间为 e(i)，离开装配线i需要的时间是x(i)。正常情况下，底盘从一条装配线的上一个站移到下一个站所花费的时间可以忽略，但是偶尔也会将未完成的底盘从 一条装配线的一个站移到另一条装配线的下一站，比如遇到紧急订单的时候。假设将已经通过装配站S(i,j)的底盘从装配线i移走所花费的时间为 t(i,j)，现在的问题是要确定在装配线1内选择哪些站以及在装配线2内选择哪些站，以使汽车通过工厂的总时间最小.
这个问题描述比较复杂, 配个图...

最优子问题,
现在对n个装配站, 需要求最优路线以达到最小通过时间. 其实这个子问题还是很容易找的, 简单的缩小规模, 考虑n-1个站的情况.
假设我们知道n-1个站的最优路线, 是否可以求得n个站的最优路线了? 答案是肯定的, 因为如果n个站的最优路线A不包含n-1个站的最优路线B, 我们就可以用B替换A中前n-1站路线达到更优, 这样和A是最优是矛盾的. 在得到n-1个站的最优路线后, 我们只需要考虑n-1到n的两种选择就可以找到全局最优解.

运行时间 , 子问题总数为n, 每个子问题要面临2个选择, 所以运行时间在O(n)

三, 无权最短路径问题和无权最长简单路径

有向图G=(V, E), 节点u, v属于V
无权最短路径问题是, 找到一条从u到v的包含最少边的路径.
无权最长简单路径, 找到一条从u到v的包含最多边的简单路径. 必须是简单, 不然有回路, 可以遍历任意次.

无权最短路径
最优子结构 ,
算法导论的思路为, 对于u,v, 并且u不等于v, 那么必定会包含中间节点w, 设u->w的最优距离为p1, w->v的最优距离为p2, 那么对于经过w点的最短路径一定为p1+p2. 那么只要考虑所有的中间节点w, 就可以找到全局的最优.
我的思路如下, 形象化一点
北京到广州, 有很多路可以选, 走哪条最快
设从北京到广州要经过1......n个城市, 北京和k个城市相连 用c(r) 1<=r<=k 表示
设f(i,j)代表从第i个城市到第j个城市的最短路径
f(1,n) = min(f(1,c(r))+f(c(r),n)) 1<=r<=k
这个思路就是分层, 先假设知道从北京到和广州相连所有城市的最优路径, 加上最后一站选择, 就可以找到最优全局路径.
运行时间 , 应该是O(n³ )

无权最长简单路径
这就给出了一个不可以使用动态规划的例子, 为什么
算法导论又一次使用了子问题独立这个短语, 误导性很强, 和前面讲分治的时候提到的完全不是一个概念.
前面的独立性指的是子问题是否重叠
这里的意思是子问题是矛盾的, 说白了, 根本就不能分成子问题去解决, 因为子问题之间是互相依赖的,共享某些资源,你用过这个节点, 我就不能再用了.
所以就无法用动态规划, 其实是无法用分治法去解决, 这个问题不能分而治之...

三, 最长公共子序列

  问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列 X=“x₀ ，x₁ ，…，x_m-1 ”，序列Y=“y₀ ，y₁ ，…，y_k-1 ”是X的子序列，存在X的一个严格递增下标序列<i₀ ，i₁ ，…，i_{k- 1} >，使得对所有的j=0，1，…，k-1，有x_i =y_j 。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。
这个多用于生物学, DNA链相同性的查找.

最优子结构 ,

问题是, 假设X = { x₁  , ... , x_m  }, Y = { y₁  , ... , y_n  }及它们的最长子序列Z = { z₁  , ... , z_k  }
思路是, 缩小问题规模来构建子结构, 
1)如果x_m =  y_n  , 即x_m =  y_n =  z_k 那么能找到{ x₁  , ... , x_m-1  }和Y = { y₁  , ... , y_n -1 }的最长子序列, 就可以得到全局解
2)如果不相等, Max({ x₁  , ... , x_m }和Y = { y₁  , ... , y_n -1 }, { x₁  , ... , x_m-1  }和Y = { y₁  , ... , y_n  })为全局最优解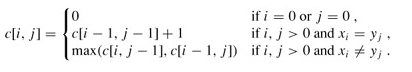

运行时间 , 应该是O(n)

四, 最优二叉查找树

问题描述：给定一个有序序列K={k1<k2<k3<,……,<kn}和他们被查询的概率P={p1,p2,p3,……,pn}，要求构造一棵二叉查找树T，使得查询所有元素的总的代价最小。
查询总代价怎么算, 把每个节点的树高*被查询概率, 再求和得到总代价. 所以必须把概率高的节点尽量放到离根近的地方, 并且还要保持二叉树的特性.
书上的例子是, 翻译, 英文翻译成法文, 需要不断通过二叉树来查询, 英语单词所对应的法语单词, 如果用一步二叉树, 效率会比较底, 比如象the这样很常用的词可能树高很高, 每次都需要logn才找到, 不合适, 所以有了这样的数据结构.

最优子结构 ,

这个和矩阵相乘的子问题划分很相似, 对于全局的最优查找树, 任一节点都可能是根, 当节点k_k 为根时, 问题被划分为(k₁ ...k_k )和(k_k+1 , k_n )的最优解. 所以只要考虑所有的节点, 就可以找到全局最优解.
运行时间 , 应该是O(n³ )

总结, 对于动态规划问题, 最难的问题就是找到最优子结构问题, 对于上面分析的例子, 找最优子结构两类思路, 一类典型思路象矩阵连乘, 和最优二叉查找树, 对问题集任意切分. 另一类思路象装配线问题, 和最长公共子序列问题, 逐步缩小问题集.

贪心算法

贪心算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中，如果旅行员每次都选择最近的城市，那这就是一种贪心算法。

对于大部分的问题，贪心法通常都不能找出最佳解（不过也有例外如求图中的最小生成树、求哈夫曼编码），因为他们一般没有测试所有可能的解。贪心法容易过早做决定，因而没法达到最佳解。例如，所有对图着色问题已知的贪心法，和所有对NP完全问题的贪心法, 都无法确保得到最佳解。然而，贪心法的好处在于容易设计和很多时能达到好的近似解。

前面说了贪心算法是普适最优化算法的一个特例, 就是说可以用贪心算法解决的问题, 一定也可以用动态规划去解决, 但反之不成立, 下面就通过两个例子来说明.

一, 活动选择问题
问题描述: 设有n个活动的集合e={1，2，…，n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间s_i 和一个结束时间f_i ,且s_i <f_i 。如果选择了活动i，则它在半开时间区间[s_i ，f_i )内占用资源。若区间[s_i ，f_i )与区间[s_j ，f_j )不相交，则称活动i与活动j是相容的。也就是说，当s_i ≥f_i 或s_j ≥f_j 时，活动i与活动j相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。

先看看使用动态规划, 最优子结构是, 如果最大集合包含活动k, 那么就可以将问题划分为两个子问题(1,k), (k+1,n), 如果知道这两个子问题的最优解, 就可以通过考虑所有k的情况来找到全局最优解. 这里k可能是从1到n的任意一个活动.

贪心法, 是怎么考虑的, 其实k不用考虑从1到n那么多种情况, 只需要考虑活动结束时间最早的那个活动, 可以证明最大的相容活动子集合一定包含活动结束时间最早的那个活动, 因为如果不包含我们可以拿他来替换集合中第一个活动, 一样是可以得到最优解. 所以可以看出贪心法就是一个特例, 当动态规划算法需要考虑n种选择的时候, 他只需要贪心的考虑当前最优的选择. 而且动态规划的选择必须考虑子问题的解, 所以它必须要自下而上的, 先从子问题开始解决. 贪心算法, 仅仅根据当前现状来进行选择, 就可以简单的自上而下的解决这个问题.

对于活动选择问题, 用贪心算法解决就很容易, 基于活动结束时间建最小堆, 不断pop活动结束时间最小的活动, 并判断是否相容, 相容的放到最大的相容活动子集合.

二, 背包问题
0-1背包问题 : 给定n种物品和一个背包。物品i的重量是w ，其价值为v ，背包的容量为c. 问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大? 在选择装入背包的物品时，对每种物品i只有两种选择，即装入背包或不装入背包。不能将物品i装入背包多次，也不能只装入部分的物品i。

部分背包问题 : 与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包。

这组问题是非常好的例子来说明什么时候应该用贪心算法, 什么时候要用动态规划.
当你可以证明局部最优就是全局最优时, 贪心算法就可以解决最优问题, 如前面的活动选择问题
对于0-1背包问题, 你可以试着用贪心算法, 先装入最值钱的, 但这样不一定时最优的, 因为可能空间会浪费. 我们在考虑是否要把一件物品加到背包中时, 必须对把该物品加进去的子问题的解与不取该物品的子问题的解进行比较, 所以典型的动态规划.
对于部分背包, 没有问题, 挑最贵的装, 可以用贪心算法, 局部最优即全局最优.

二, 赫夫曼编码

赫夫曼编码是一种被广泛应用而且非常有效的数据压缩技术, 一般编码技术对所有字符采用相同的位数编码, 如ascii码, 8bit. 而赫夫曼编码对高频词采用较少位数编码, 而低频词采用较高位数编码, 从而达到数据压缩, 见下图的例子.

为了变长编码, 所以采用前缀编码技术, 没有一个编码是另一个编码的前缀. 赫夫曼设计了一个可用来构造一种称为赫夫曼编码的最优前缀码的贪心算法。算法很简单, 总是把最小两个节点合成子树, 这就是贪心算法. 有了赫夫曼树, 自上而下解码, 自下而上编码.