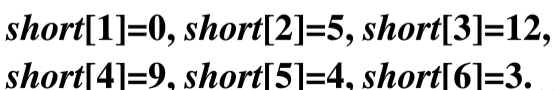单源最短路径算法——Bellman-ford算法和Dijkstra算法
BellMan-ford算法描述
1.初始化:将除源点外的所有顶点的最短距离估计值 dist[v] ← +∞, dist[s] ←0;
2.迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
3.检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 dist[v]中。
举例说明:
给定原点是s,初始化时候除了原点s之外,其他的都是无穷大的。因为有5个顶点,所以需要松弛的次数为5-1次
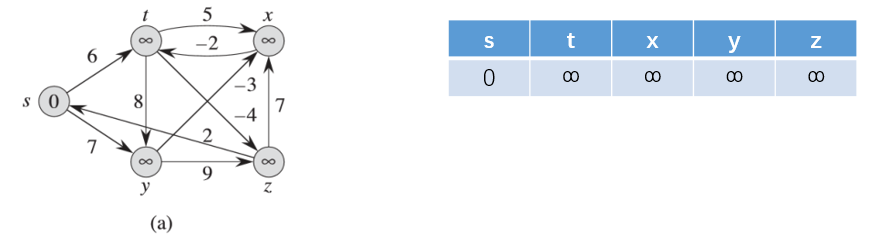
这里我们按照边<t,x>、<t,y>、<t,z>、<y,x>、<y,z>、<z,x>、<z,s>、<s,t>、<s,y>的顺序进行变得松弛操作。
第一次按照上述边进行松弛操作之后(实际上只对<s,t>、<s,y>进行操作)的结果为
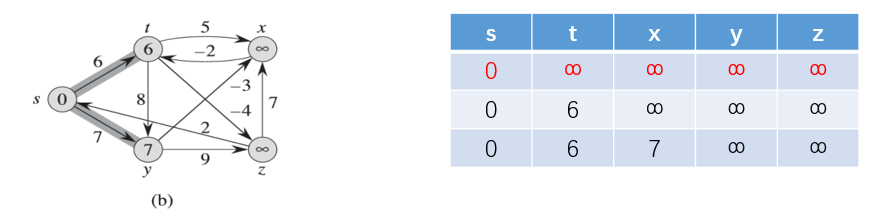
第二次按照给定边进行松弛操作之后:
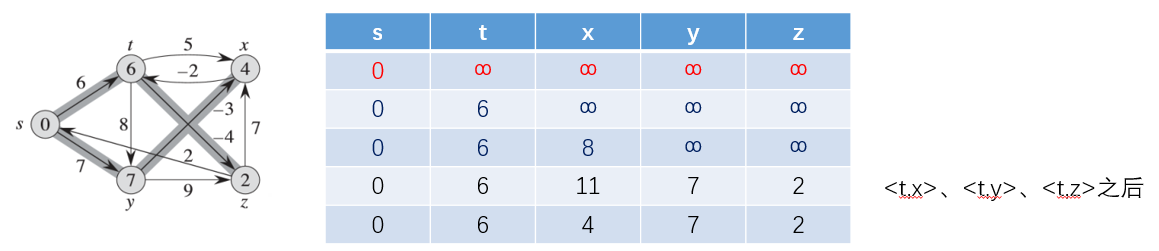
第三次松弛操作之后:
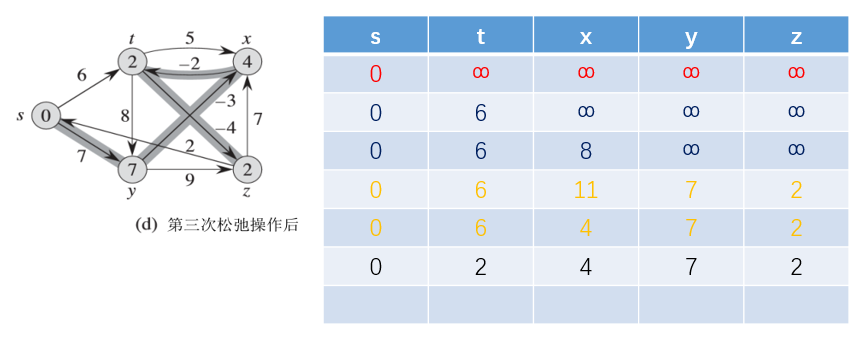
最后一次松弛操作:
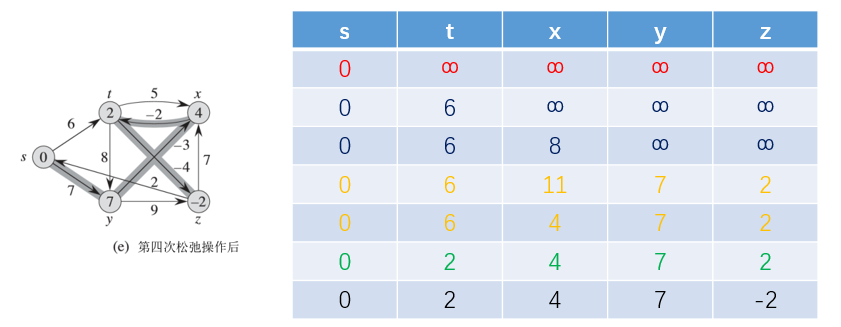
给出实力代码

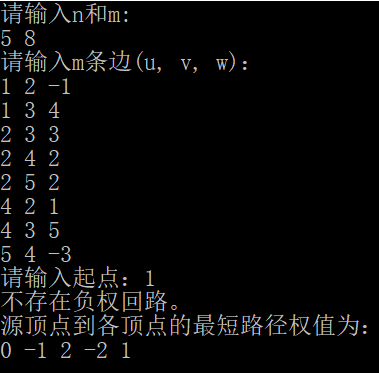
1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 5 #define INF 0xffff //权值上限 6 #define maxe 5000 //边数上限 7 #define maxn 100 //顶点数上限 8 int n, m; //顶点数、边数 9 int d[maxn]; //保存最短路径权值的数组 10 int parent[maxn]; //每个顶点的前驱顶点,用以还原最短路径树 11 struct edge //表述边的结构体,因为要对每一条边松弛 12 { 13 int u, v, w; //u为边起点,v为边端点,w为边权值,可以为负 14 }EG[maxe]; 15 16 bool Bellman_Ford(int s) //计算从起点到所有顶点的 17 { 18 for(int i = 1; i <= n; i++) //初始化操作d[EG[j].v] > d[EG[j].u]+EG[j].w 19 { 20 d[i] = INF; 21 parent[i] = -1; 22 } 23 d[s] = 0; 24 bool flag; //标记,判断d值是否更新,跳出外层循环的依据 25 for(int i = 1; i < n; i++) //外层循环最多做n-1次 26 { 27 flag = false; //初始为false,假设不需再更新 28 for(int j = 0; j < m; j++) //对m条边进行松弛操作,若有更新,flag记为true 29 if(d[EG[j].v] > d[EG[j].u]+EG[j].w) //if d[v] > d[u] + w(u, v),更新d[v] 30 { 31 d[EG[j].v] = d[EG[j].u]+EG[j].w; 32 parent[EG[j].v] = EG[j].u; 33 flag = true; 34 } 35 if(!flag) break; //若松弛完每条边后,flag状态不变,说明未发现更新,可直接跳出循环 36 } 37 for(int i = 0; i < m; i++) //做完上述松弛后,如果还能松弛,说明存在负权回路,返回false 38 if(d[EG[i].v] > d[EG[i].u]+EG[i].w) 39 return false; 40 return true; //不存在负权回路,返回true 41 } 42 43 int main() 44 { 45 int st; 46 printf("请输入n和m:\n"); 47 scanf("%d%d", &n, &m); 48 printf("请输入m条边(u, v, w):\n"); 49 for(int i = 0; i < m; i++) 50 scanf("%d%d%d", &EG[i].u, &EG[i].v, &EG[i].w); 51 printf("请输入起点:"); 52 scanf("%d", &st); 53 if(Bellman_Ford(st)) 54 { 55 printf("不存在负权回路。\n"); 56 printf("源顶点到各顶点的最短路径权值为:\n"); 57 for(int i = 1; i <= n; i++) 58 printf("%d ", d[i]); 59 printf("\n"); 60 } 61 }
输入测试用例
1 2 -1
1 3 4
2 3 3
2 4 2
2 5 2
4 2 1
4 3 5
5 4 -3
Dijkstra算法
(1)该算法要求所有边的权重均为非负值,即对于所有的边(u,v)∈E,ω(u,v)≥0,—— 既不能有负权重的边,更 不能 有负权重的环。算法在运行过程中维持的关键信息是一组结点集合S。从源结点s到该集合中每个节点之间的最短路径已经被找到。算法重复的从结点集合V-S中选择最短路径估计最小的结点u,将u加入到集合S中,然后对所有从u发出的边进行松弛操作。
(2)算法设计思想如下:

(3)算法描述伪代码如下:

(4)下面给出算法一些理解:
上述算法第一行执行的是d值和π值的初始化,第2行将集合S初始化为一个空集。算法所维持的循环不变式为Q=V-S,不变式在算法的while循环中保持不变。
第3行对最小优先队列进行初始化,将所有的结点V都放在队列里面。此时的S=∅。
在执行while循环的时候,从集合Q=V-S中抽取结点u,第6行将该结点加入到结合S里面,从而保持不变式成立。
然后将从u结点出发的所有结点进行松弛操作。如果一条经过结点u的路径能够使得从源结点s到结点v的最短路径权重比当前的估计值更小,就对v.d的数值和前驱结点进行更新操作。
(5)下面是一个实例
输入G,源结点1,结点集合V=<1,2,3,4,5,6>
①从源结点开始,此时集合S中只有结点1,从1出发的结点有6、2,所以更新此时的dist[2]和dist[6]的数值

②选择dist[2]和dist[6]中最小的值,即dist[6]=3,将结点6加入到集合S中,然后从更新结点6出发的结点2、5、4的路径值,分别更新为dist[2] = 5、dist[5] = 4、dist[4] = 9。
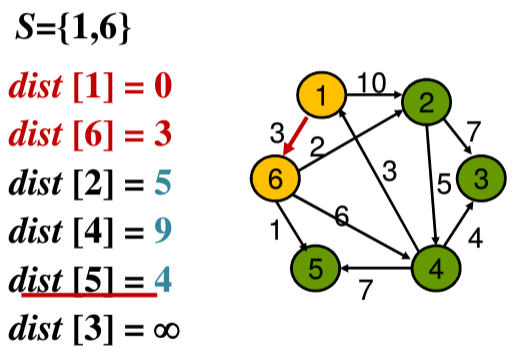
③选择dist[2] = 5、dist[5] = 4、dist[4] = 9中最小的值,即dist[5] = 4,将结点5加入到结合S中,然后更新从结点5出发的结点的值,由于没有从结点5出发的结点,所以直接进行下一步
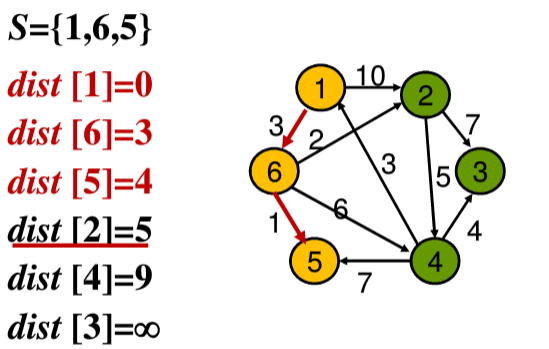
④第三步中选择dist[2] = 5,将结点2加入集合S中,然后更新从结点2出发的结点3、4的值,分别为dist[3] = 12、dist[4] = 9
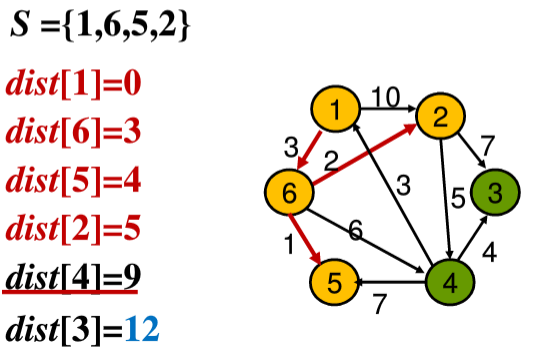
⑤从剩下的两个结点3、4中选择dist更小的结点4,将结点4加入集合S中,然后更新从结点4出发的结点3的值,判断之后,发现dist[3]依旧还是12
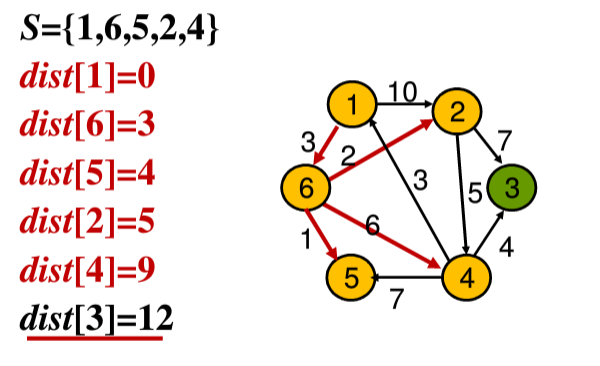
⑥最后一步,将结点3加入集合S中,此时以及更新完毕,找到了从结点1到达所有节点的最短路径