疯狂位图之——位图扩展随机数

　　这篇文章主要介绍随机数，不过这次讲述的随机数是从上两篇的延伸出来的，所以还是继续疯狂位图的标题，欢迎看完本文拍砖。

一、实现需求

　　利用C语言提供的rand()函数构造一个随机函数randLong()，能够生成0-(2^31-1)之间的随机整数。rand()生成的随机整数在0-(2^15-1)范围内。可以参考上一篇的位图生成数据。

二、利用位图的方法

　　起初我以为很简单:

void randLong(){
    return 1.0*rand()/RAND_MAX*LONG_MAX;
}

　　后来受五岳的文章启发，发现我犯了严重的错误，rand()的取值空间中只有2^15-1=32767个整数，按上面的方法只是在0-(2^31-1)上抽取了一小部分数。如果说rand()生成的是0-32767直接的随机浮点数而不是整数的话，上面的办法扩展随机数的范围是可行的。

　　因为一直在整位图，所以在想能不能从位入手，实现随机数的扩展。我都有点感受到位图的强大了，还真想出了一个用位图扩展的方法，这里不再拐弯抹角，直接上菜：

　　需要生产的随机数是[0-(2^31-1)]的闭区间内，端点值化成2进制后为：

0: 0000,0000,0000,0000，0000,0000,0000,0000
     ...
     ...
     ...
2^31-1:0111,1111,1111,1111,1111,1111,1111,1111　

　　看到这个二进制后，相信你已经有想法了。我们申请一个32位长整型的位图，将位图每一位初始化为0，这时候我们需要一个rand1()生产0,1的随机数，对每个位调用一次random=rand1()，如果random=1就把该位设置为1，如果为random=0则设置为0，调用31次(除最高位为0不需要随机选择)后，这个长整型变量的值就是我们需要的随机数。

　　如果rand1()足够随机，即等概率(1/2)的生成0、1，那么我们按上面的方法的得到的任意一个数的概率都为(1/2)^31。来看一下实现代码：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

/*******生成0、1的随机产生器********/
short rand01(){
    return rand() % 2;
}
/********将bit所在位设置为1**********/
void setOne(long * p, short bit){
    *p |= 1<<bit;
}
/********将bit所在位设置0**********/
void setZero(long *p, short bit){
    *p &=~(1<<bit);
}
/*******生成0-2^bitNum-1之间的随机数**************/
long randLong(short bitNum){
    long a = 0;
    long *p = &a;    
    for(short i= 0;i < bitNum; i++){
        short bit = rand01() % 2;
        if(bit == 0)
            setZero(p,i);
        else
            setOne(p,i);
    }
    return *p;
}

　　randLong(short bitNum)可以生成0到2的任意幂次方之间的随机数(当然bitNum<=31)，生成的随机数基本上等概率的。我们可以测试一下生成0-7的随机数概率：

void main(){
    const int max = 8;
    int count[max];
    for(short i=0;i<max;i++)
        count[i] = 0;
    long num=10000000;    
    for(long i=0;i<num;i++){
        long index = randLong(3);//生成0-(2^3-1)的随机数
        count[index]++;//计数    
    }
    for(short i=0;i<max;i++)
        printf("%d:\t%lf\n",i,1.0*count[i]/num);//输出概率    
}

　　输出的结果如下：　

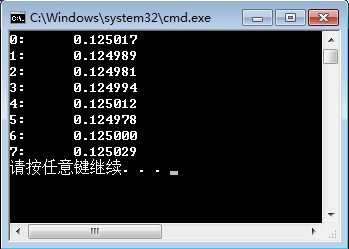
　　进行了1000万次试验，发现每个数的概率还是很接近1/8=0.125的。

三、递归实现的方法

　　上面有位图的方法，每次生成一个随机数需要调用多次rand01()，速度略微慢些，这里再提供一个基于递归的实现方法，直接上代码：

/**********根据rand()构造[0,max]的闭区间的随机整数**********/
long random(long max){
    if(max <= RAND_MAX)//RAND_MAX是rand()的最大值，值为0x7fff
        return rand()% (max+1);//直接得到[0,max]的随机数
    else
        return (random(max/(1+RAND_MAX)) * (1+RAND_MAX) + rand()) % (max+1);//递归得到[0,max]的随机数
}

   　当max<=RAND_MAX时，对rand()模余就得到了[0,max]的随机数;

　　当max>RAND_MAX时，我们先来看 (random(max/(1+RAND_MAX)) * (1+ RAND_MAX) + rand()) ，令k=max/(1+RAND_MAX)，即k表示max是(1+RAND_MAX)的倍数向下取整，前面的式子变为(random(k) * (1+RAND_MAX)+ rand())。这里为了方便说明，我们假设rand()生成[0,4]的整数（即RAND_MAX=4），max=52,于是k=52/(1+4)=10，相当于把[0,52]分成10个区间，根据定义random(10)生成的是[0,10]的整数，random(10)*5相当于随机的定位到每个区间的开始位置，再加上一个rand()，即在左端点上加一个随机的偏移量构成一个新的随机数，而10依然大于4，需要用同样的方法生成random(10)。可以结合图来理解：　　

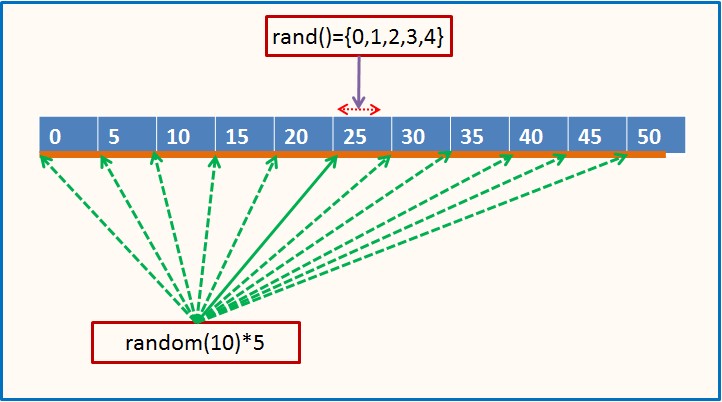
　　最后还需要将(random(10) * 5+ rand())对53模余，因为两个相加的结果可能会大于52，模余53可以保证生成的数在[0,52]范围内，注意是模余53不是52。

　　有了上面的方法我们可以进一步改进，生成任意区间上的随机整数，代码如下：

/*******根据c语言提供的rand()生成long型的任何区间随机整数值*******/
long random(long min,long max){
    if(max <= RAND_MAX)
        return min + (rand()%(max - min + 1));
    else
        return min + ((random(max/(1+RAND_MAX)) * (1+RAND_MAX) + rand()) % (max-min+1));
}

 　　我们来测试一下区间随机数：

void testRandom(){
    long min = 234567;
    const short num = 9;
    long count[num+1];
    for(short i=0;i<=num;i++){
        count[i]=0;
    }
    long testTimes = 10000000;//试验次数
    for(long i=0;i<testTimes;i++)
        count[random(min,min+num)-min]++;//计数器
    for(short i=0;i<=num;i++)
        printf("%d:\t%lf\n",i+min,1.0*count[i]/testTimes);//输出概率    
}

　生成了[234567,234567+9]之间的10个数，运行的结果如下：

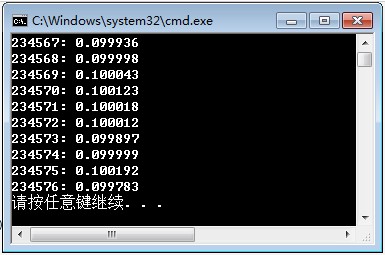
　　每个数出现的概率非常接近1/10=0.1，可以认为是等概率生成。

　　前面我们说过，模余可以保证生成的数不超过范围内，但会造成概率不相等的情况，特别是在用大的rand()生成小的随机数时，我们测试一下，用rand7()构造rand4()，rand7()生成[0,7]的整数，rand4()生成[0,4]的整数，看如下代码：

int rand7(){//生成0到7的整数
    return rand()%8;
}
int random4(){//生成0到4的整数
    return rand7() % 5;
}
void main(){
    const int max = 5;
    int count[max];
    for(short i=0;i<max;i++)
        count[i] = 0;
    long num=10000000;    
    for(long i=0;i<num;i++){
        count[random4()]++;//计数    
    }
    for(short i=0;i<max;i++)
        printf("%d:\t%lf\n",i,1.0*count[i]/num);//输出概率
}

　　输出的结果如下：

　　

　　我们可以看到进行1000万次试验，生成0、1、2的概率约为0.25=1/4，而3、4的概率约为0.125=1/8，这两组之间的概率相差一倍，为什么会这样？稍加分析，我们就知道了，rand7()生成的数为[0,1,2,3,4,5,6,7]，且是等概率的生成这8个数，模余5后的结果为[0,1,2,3,4,0,1,2]，所以rand4()中的0,1,2即有可能来自[0,1,2,3,4,5,6,7]中的0,1,2，也可能来自5,6,7，而rand4的3,4只能由rand7()的3,4而来。所以会出现0,1,2的概率是3,4概率的两倍，一般的测试实验可以不用考虑，在需要严格的随机测试实验时，应当注意这个问题。用到模余的地方都有可能造成概率不等的情况，要想写一个通用的概率相等的random(m,n)是一个数学难题。

　　挂羊头卖狗肉了，这篇主要讲述随机数的一些东西，也牵扯到了些位图。

　　补充：后来想到用位运算扩展C语言的rand()到long范围内的randLong()，其实可以用位移运算，只需要调用rand()就可以了，看代码：

/*********通过移位来构造长整型的随机数***************/
long randLong(){
    long r = (long)rand();
    return (r << 16)+ rand();
}

  　这个比调用31次都rand01()快很多，而且只要rand()是等概率的，生成的randLong()也是等概率的。

　　感谢关注，欢迎评论。

　　转载请注明出处：http://www.cnblogs.com/fengfenggirl