多项式求导设计分析

多项式求导设计分析

一、第一次作业

1. 作业需求

• 设计一个能完成简单多项式求导的程序，多项式中包括带符号整数和幂函数，输出要求在保证正确的情况下尽可能短。

2. 实现方案

• 这次作业我用了两个类，Number 和 Test1 ，前者是作为每一个单独的项，后者作为 main 函数运行。
• 这次的检查输入格式所用的是大正则匹配，如下代码：

Pattern p1 = Pattern.*compile*("[ \\t]*+" +
        "([ \\t]*+((([[+]-][ \\t]*+[[+]-])|" +
        "([[+]-][ \\t]*+)|([ \\t]*+))" +
        "(\\d++[ \\t]*+\\*)?[ \\t]*+x[ \\t]*+" +
        "(\\^[ \\t]*+[[+]-]?\\d++[ \\t]*+)?)|" + // 含 x
        "((([[+]-][ \\t]*+[[+]-])|" +
        "([[+]-][ \\t]*+)|([ \\t]*+))\\d++)[ \\t]*+)" + //整数
        "[ \\t]*+" +
        "([ \\t]*+((([[+]-][ \\t]*+[[+]-])|([[+]-][ \\t]*+))" +
        "(\\d++[ \\t]*+\\*)?[ \\t]*+x[ \\t]*+" +
        "(\\^[ \\t]*+[[+]-]?\\d++[ \\t]*+)?)|" +
        "((([[+]-][ \\t]*+[[+]-])|([[+]-][ \\t]*+))\\d++)[ \\t]*+)*+" +
        "[ \\t]*+");

• 这种检查输入的方法优点是只需要一个表达式，比较方便，缺点是检查起来非常麻烦，几乎没有可读性，所以第二次作业我采用了分块匹配的方法。
• 求导的思路和第一次上机实验中矩阵的运算类似，每次从输入中获取一个项，在 Number 类中分析项的构成简化为 a*x^b 的算式，再用简单的求导规则进行求导，把结果以 (a,b) 的形式存入一个 ArrayList 中，同时在存入的过程中判断是否有相同的项进行合并；最后在 main 函数中进行输出。
• 由于第一次作业我只采用了一个文件中的两个类，所以 UML 几乎没有意义，将在下次作业中体现。

3. 优缺点分析

• 优点：
  • 在刚刚接触面向对象这种编程方式时，没有以惯用的面向过程的方式来编写这个程序，而是参照实验课中矩阵运算的程序，把程序构造为两个类，负责不同的功能。
• 缺点：
  • 由于对 Java 程序的不熟悉，在构造两个类时，没有把它们分为不同的文件，导致我的代码风格分没有得到满分；
  • Number 类还是太长，内部还是有部分面向过程的编程思想；
  • 命名不规范，虽然最后按照代码风格修改成符合要求的命名，但是命名几乎没有什么实际含义。

4. 分析 Bug

• 这次作业因为涉及到大整数，int 和 long 将不适用，所以用 BigInteger 代替，但是在最后优化的判断正负中，我使用了intValue 方法将 BigInteger 数转为 int 型再判断正负，会出现超过 int 型的数据范围的情况导致判断错误，所以在大整数的测试点中几乎全部没过。

二、第二次作业

1. 作业需求

• 设计一个能完成简单幂函数和简单三角函数的求导，相比于第一次作业，因子增加了 sin(x) 和 cos(x) 和它们的乘方，并且因子之间可以相乘，输出同样要求在正确的情况下尽可能短。

2. 实现方案

• 这次的作业，我依然用了两个类，PolyDiff 和 Term ，不过这次的两个类我放在了不同的文件中。
• 检查多项式输入格式的方法，我摒弃了大正则，改为使用按照因子、项、表达式的方法依次匹配，代码段如下：

String factor = "(([ \\t]*+[[+]-]?\\d+[ \\t]*+)|" + //整数
        "([ \\t]*+x([ \\t]*+\\^[ \\t]*+[[+]-]?\\d+)?[ \\t]*+)|" + //幂函数
        "([ \\t]*+(sin|cos)[ \\t]*+[(][ \\t]*+x[ \\t]*+[)]([ \\t]*+" +
        "\\^[ \\t]*+[[+]-]?\\d+)?[ \\t]*+))"; //三角

String term = "[[+]-]?" + factor +
        "([ \\t]*+[*][ \\t]*+" + factor + ")*+";
String form = "[ \\t]*+[[+]-]?[ \\t]*+" + term +
        "([ \\t]*+[[+]-][ \\t]*+" + term + "[ \\t]*+)*+";
Pattern formFormat = Pattern.*compile*(form);

Matcher m1 = formFormat.matcher(str);
	

• 用这种方法匹配字符串，可以在检查时方便定位问题， 精确定位错误到每一个部分。
• 下图是第二次作业的 UML 图：

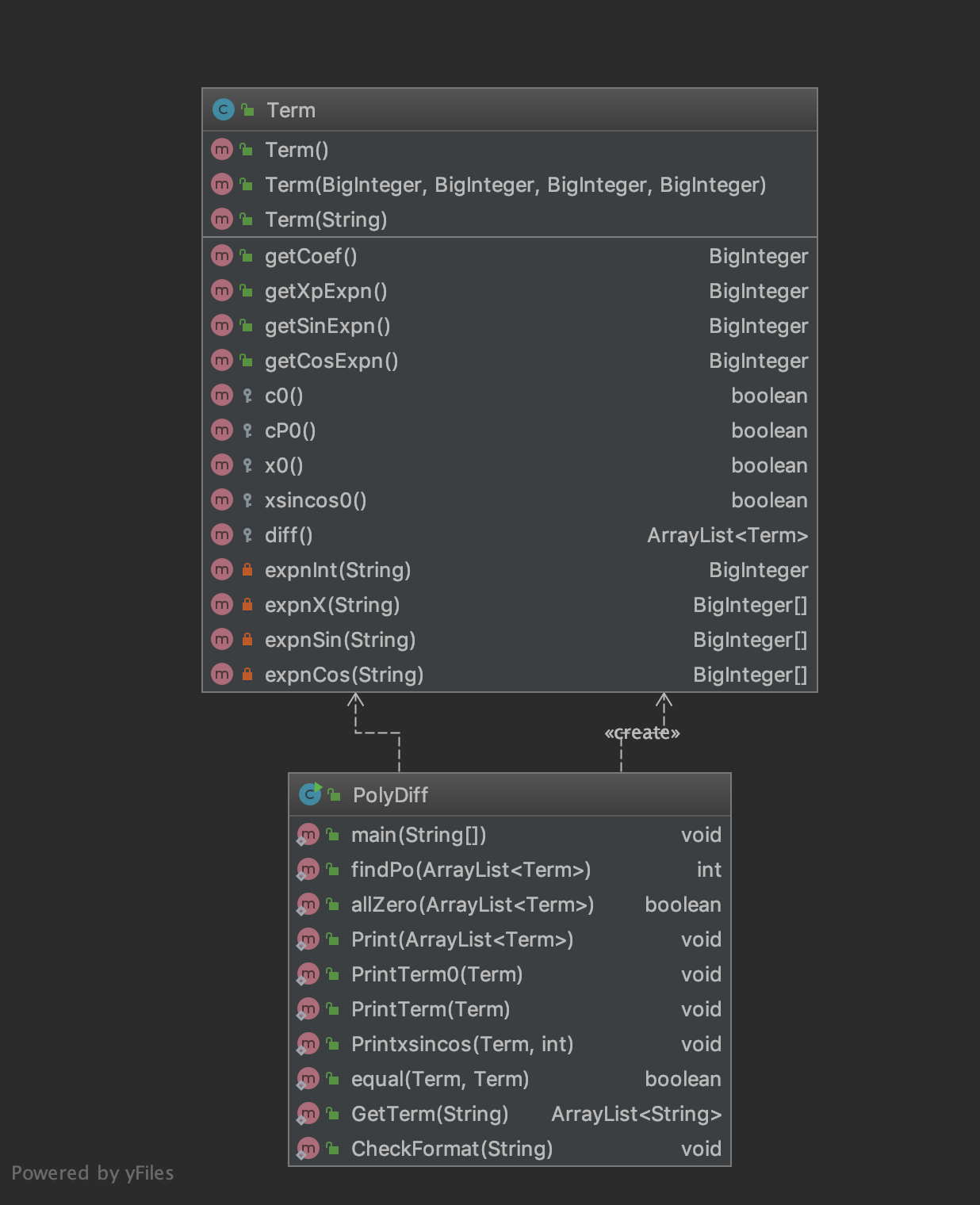
• 这一次的求导我用的方法和上次类似，把输入中的每一项分离出来，作为 Term 类，化简为 k * x^a * sin(x)^b * cos(x)^c 的形式，然后运用数学公式进行求导，直接把 (k, a, b, c) 代入求导所得的数学公式，再经过在 ArrayList 中合并同类项的过程，最后在 main 函数中完成输出。

三、Bug 分析

• 这次作业的 Bug 在互测中被发现了，而通过了强测；此次的 Bug 在于当 +1 或 -1 不作为第一项输出时，会仅仅输出一个正号或符号，这是由于我程序把输出第一项与其他分离开来处理，同时程序又涉及得不合理导致的，在 Bug 修复中比较容易将它修改过来。

三、第三次作业

1. 作业需求

• 设计一个能完成多项式求导的程序，多项式包括 sin(x)、cos(x) ，以及它们三角函数的嵌套，还包括第二次作业的所有因子。

2. 实现方案

• 这次作业的 UML 图如下：
  

• 这个项目我一共设计了五个类，Main 类负责读入、递归求导以及输出，CheckFormat 类负责检查输入的表达式的格式，Bracket 类负责在检查格式时递归匹配左右括号，SimFactor 类负责在递归求导中对简单因子进行求导，Triornot 类负责判断因子是否是三角函数因子。

• 下面我来分析这个程序中我写的比较巧妙的两处：

  • CheckFormat 类中由于因子中可以嵌套表达式因子，所以无法直接写出因子、项、表达式的正则匹配式子，这里我采用了，匹配因子时如果检测到括号，只需匹配左右括号中有内容即可，然后在匹配到相关非三角函数的括号的时候，检查括号中是否和表达式匹配，相关代码段如下：

private String factor = "(([ \\t]*+[[+]-]?\\d+[ \\t]*+)|" + //整数
        "([ \\t]*+x([ \\t]*+\\^[ \\t]*+[[+]-]?\\d+)?[ \\t]*+)|" + //幂函数
        "([ \\t]*+(sin|cos)[ \\t]*+[(].+[)]([ \\t]*+" + //三角
        "\\^[ \\t]*+[[+]-]?\\d+)?[ \\t]*+)|" +
        "[ \\t]*+([(].+[)]))[ \\t]*+";

private Pattern paFactor = Pattern.*compile*(factor);

private String term = "[[+]-]?" + factor +
        "([ \\t]*+[*][ \\t]*+" + factor + ")*+";
private String form = "[ \\t]*+[[+]-]?[ \\t]*+" + term +
        "([ \\t]*+[[+]-][ \\t]*+" + term + "[ \\t]*+)*+";

private Pattern formFormat = Pattern.*compile*(form);
		

* 在递归求导的相关代码中，我想通过加减号将表达式分为项的集合，在通过乘号将项分为因子的集合，通过返回其求导的字符串来完成递归求导，如碰见对表达式因子求导，则调用表达式求导的方法对括号中的表达式求导。
* 由于这次作业我用的是递归求导的方法，所以采用了获取到导数的字符串就直接输出的方法，并没有进行任何优化，这是我本次作业的一个缺点。

3. Bug 分析

• 在匹配表达式因子的时候，我忘记在两侧加上 [ \\t]*+ 导致在匹配表达式因子时两侧有空字符时会匹配错误；
• 三角函数中出现带符号整数的情况只匹配负数。

四、从别人程序中发现的 Bug

• 大多数是匹配输入的问题，应该输出 WRONG FORMAT! 的时候反而输出了求导的结果；
• 第三次作业有的同学像我一样忘记匹配括号两侧的空格。

五、总结

• 这一单元的三次作业让我对 Java 这种编程语言有了全新的认识，同时老师和助教们的严格要求也让我对代码风格、程序可移植性有了更深的思考。当然我写出来的代码仍然不够优雅和美观，在今后的 Java 作业中仍需努力。