Douglas Peucker算法的C#实现

一、算法原理

Douglas-Peucker算法

在数字化过程中，需要对曲线进行采样简化，即在曲线上取有限个点，将其变为折线，并且能够在一定程度

上保持原有的形状。

经典的Douglas-Peucker算法描述如下：

（1）在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；

（2）得到曲线上离该直线段距离最大的点C，计算其与AB的距离D；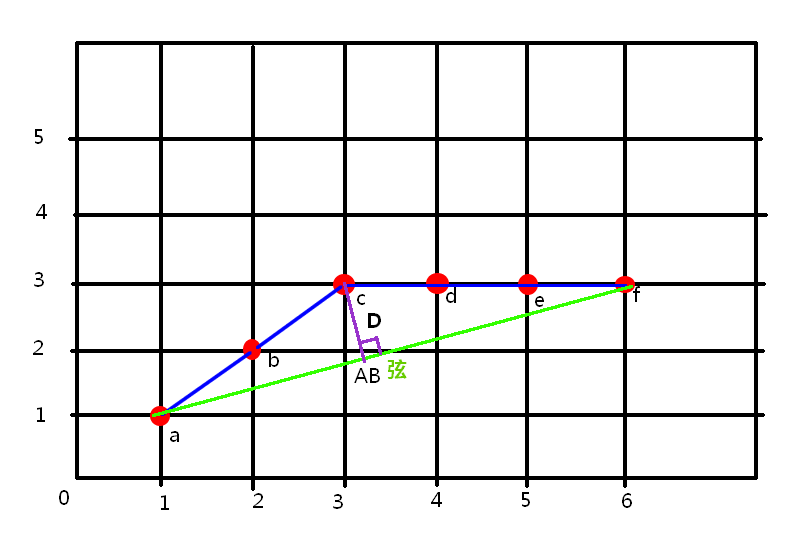

（3）比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。

（4）如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。

（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。

 

二、算法C#实现

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace ConsoleApplication2
{
    public struct cvPoint
    {
        public int X;
        public int Y;
        public cvPoint(int x, int y)
        {
            X = x;
            Y = y;
        }
    }
    class Program
    {
        static void Main(string[] args)
        {
            var points = new List<cvPoint>();
            points.Add(new cvPoint(1, 1));
            points.Add(new cvPoint(2, 2));
            points.Add(new cvPoint(3, 3));
            points.Add(new cvPoint(4, 3));
            points.Add(new cvPoint(5, 3));
            points.Add(new cvPoint(6, 3));
            points.Add(new cvPoint(5, 3));
            points.Add(new cvPoint(6, 3));
            points.Add(new cvPoint(7, 3));
            points.Add(new cvPoint(8, 3));
            var epsilon = 0.8d;
            var filteredPoints = new List<cvPoint>();
            DouglasPeucker(points, epsilon, ref filteredPoints);
            Console.WriteLine("Filtered points：");
            foreach (var f in filteredPoints)
            {
                Console.WriteLine(string.Format("{0},{1}", f.X, f.Y));
            }
            Console.ReadKey();
        }
        private static double distanceToSegment(cvPoint p, cvPoint start, cvPoint end)
        {
            var m1 = ((double)(end.Y - start.Y)) / ((double)(end.X - start.X));
            var c1 = start.Y - m1 * start.X;
            var interPointX = 0d;
            var interPointY = 0d;
            if (m1 == 0)
            {
                interPointX = p.X;
                interPointY = c1;

            }
            else
            {
                var m2 = -1 / m1;
                var c2 = p.Y - m2 * p.X;
                interPointX = (c1 - c2) / (m2 - m1);
                interPointY = m2 * interPointX + c2;
            }
            return Math.Sqrt(Math.Pow(p.X - interPointX, 2) + Math.Pow(p.Y - interPointY, 2));
        }

        private static void DouglasPeucker(IList<cvPoint> PointList, double epsilon, ref List<cvPoint> filteredPoints)
        {
            var dmax = 0d;
            int index = 0;
            int length = PointList.Count;
            for (int i = 1; i < length - 1; i++)
            {
                var d = distanceToSegment(PointList[i], PointList[0], PointList[length - 1]);
                Console.WriteLine(string.Format("{0}.distence:{1}", i, d));
                if (d > dmax)
                {
                    index = i;
                    dmax = d;
                }
            }
            Console.WriteLine(string.Format("dMax:{0}", dmax));
            // If max distance is greater than epsilon, recursively simplify
            if (dmax > epsilon)
            {
                filteredPoints.Add(PointList[0]);
                filteredPoints.Add(PointList[index]);
                filteredPoints.Add(PointList[length - 1]);
                DouglasPeucker(PointList.Take(index + 1).ToList(), epsilon, ref filteredPoints);
                DouglasPeucker(PointList.Skip(index + 1).Take(PointList.Count - index - 1).ToList(), epsilon, ref filteredPoints);
            }
        }
    }
}

 

三、算法验证
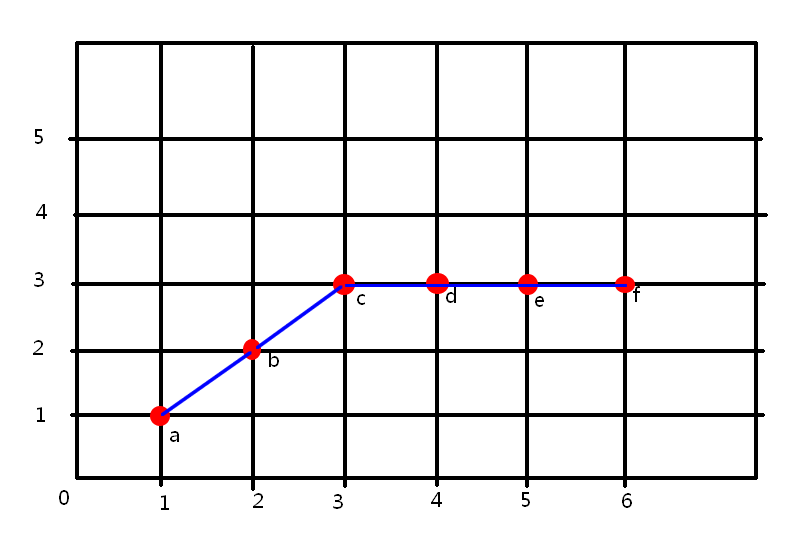
近似前：

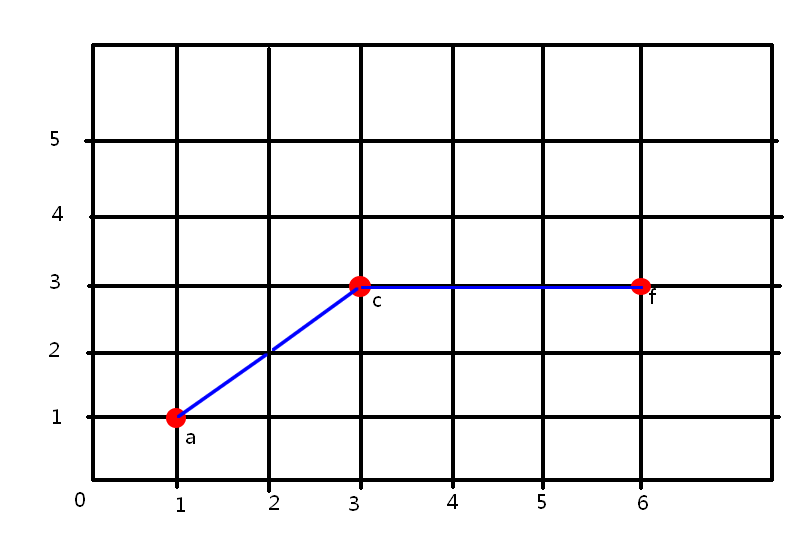
近似后的线段：

 

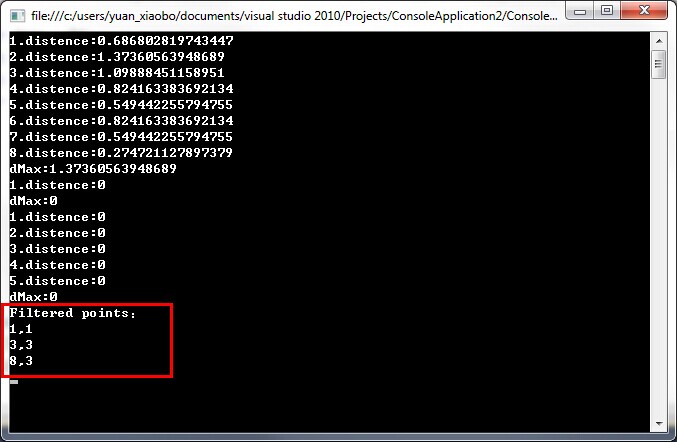
本文地址： http://www.cnblogs.com/deepleo/p/Douglas-Peucker.html

参考：http://www.codeproject.com/Articles/18936/A-C-Implementation-of-Douglas-Peucker-Line-Approxi