Matrix Tree
（更为基本的知识本篇不作讲解）
Kirchhoff矩阵：定义为度数矩阵减去邻接矩阵。
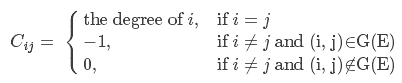
MatrixTree定理为：G的所有不同的生成树的个数等于C中任何一个n−1阶主子式。
我们把这个主子式对应的矩阵记为Cr，表示从C中删去了第r行和第r列后得到的矩阵。
性质1：对于任何一个图G，它的Kirchhoff矩阵C的行列式总是0。这是因为C每行每列所有元素的和均为0。
性质2：如果G是不连通的，则它的Kirchhoff矩阵C的任一个n−1阶主子式的行列式均为0。
证明：如果G中存在k(k>1)个连通分量G1,G2,…,Gk，
那么，我们可以重新安排Cr的行和列使得属于G1的顶点首先出现，然后是G2，以此类推。
因为行列都需要交换，所有总交换次数是偶数，行列式不变。
假设我们从中删去的第r行对应的点所在的连通分量是Gt，把第r个点从Dt中删去后得到的矩阵为Dtr。
那么，根据这个图的性质，我们得到如下的C矩阵
D1,D2,…,Dk表示各连通分量的C矩阵，由性质1，∀i∈[1,k],Di=0。所以Cr矩阵的行列式为
因为k>1，因此至少还有一个det(Di)被计算，所以det(Cr)=0
性质3：如果G是一棵树，那么它的Kirchhoff矩阵C的任一个n−1阶主子式的行列式均为1。
这是我们证明的关键部分之一，它和生成树的计数有关。
证明：我们对C进行三步处理，假设删除的点为r。
第一步：我们以r为根，把所有的顶点按深度重新编号。显然，在刚才得到的顺序中，一个点的父亲必然出现在这个点之前。
第二步：将Cr的n−1行和n−1列按照刚才得到的顺序重新排列。因为行列都需要交换，所有总交换次数是偶数，行列式不变。
第三步：按照刚才得到的顺序的逆序处理，对于每个点y，如果y的父亲x不等于r，则把第y列加到第x列上去。
这样处理后Cr会变成上三角矩阵并且主对角线上所有的数字都是1。这就证明了我们的结论。
现在引入无向图G的关联矩阵B，是一个n行m列的矩阵，行对应点而列对应边。
我们先假设E={e1,e2,…,em}。那么B可定义为
（因为这里是无向边，所以其实只要满足ej中的两个点一个为1，另一个为−1即可）
由于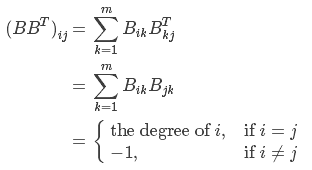
所以C=B·BT。
设Br为B去掉第r行后得到的新矩阵，易知Cr=BrBrT。
又设BrF是把Br中不属于边集F的列删除后形成的新矩阵，同样的方式定义CF矩阵。
那么也可易得
。
接下来就能推最后的Matrix Tree定理了
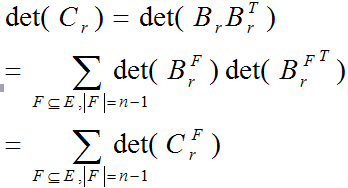
因为|F|=n-1 所以，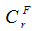
要么是树，要么不联通，所以对于生成树个数的贡献就是1或0。
证毕。
Matrix Tree定理的推广情况
①至于有重边的情况，可以发现重边对前面的推导没有任何影响，所以只要在基尔霍夫矩阵中计重边数就可以了。
②但是有向图，要将定理和方法修改，再证(我并不会啊。。) ——这里的计数是指 “由根能到达所有点的树形图”的计数
下面讲述 推广到有向图后的Matrix Tree定理 的变化：
首先邻接矩阵改成只记出边，度数矩阵改成了只记入度，然后现在得到的基尔霍夫矩阵的主余子式 Cr 代表了以 r 为根的有向生成树个数。
性质一：这下基尔霍夫矩阵的变化比较明显，它不是对称的了，并且它的每行元素的和也不再一定是 0 了（现在是一个点的入度减去出边数）。
但是好在每一列的和还是 0，所以最重要的性质还没有改变，仍然可以全部行加到一行上来证明它的行列式为 0 。
性质二：不连通的图的基尔霍夫矩阵的主余子式的值为 0 这一条出现了改变，变成如果从 r 点出发不能到达所有点，则 Cr=0。
性质三：从根出发能到每一个点的树形图的基尔霍夫矩阵的主余子式的值为1,。
证法是类似的(不证啦啦啦啦。。)
计数的时候原理没有变化，仍然成立。大致就是这样推广到有向图上。
另外这和重边的推广没有什么冲突，so依然可以结合在一起。
有向图欧拉回路计数
首先验证每个点出入度是否平衡，之后随便取个点作为起点，求内向树形图（外向也一样）计数。
如果问的是 欧拉回路的路径走法计数，则在每个分岔点 乘一个阶乘，即Ans乘上 除根外每个点的（度数-1）的阶乘，以及根的度数的阶乘。（因为 除根外，每个点有一个度是朝向根的，所以要减一）
有向图欧拉路计数
转化成上一个问题即可。
