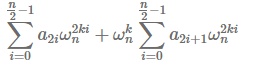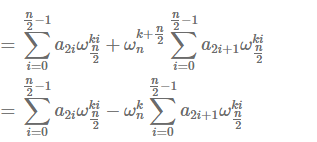从多项式乘法到快速傅里叶变换

推荐阅读：http://blog.miskcoo.com/2015/04/polynomial-multiplication-and-fast-fourier-transform

这里写写自己对快速傅里叶变换的一点理解。

 

 

快速傅里叶变换的出发点，是多项式的点值表示

这里运用的其实是离散傅里叶变换，即DFT

DFT

在ruanx.pw的一篇博文上，有这样的图片

我们发现从两者的点值表达到答案的点值表达可以通过时间复杂度完成

那么考虑系数与点值之间的转化方式

CLRS上提供了一种很好的方式，也是常用方法之一

根据

且复平面上的单位根的复数解为

此时

我们得到几个性质

互不相等

性质三的证明请自己进行推导。

后来我们发现一般情况下具有这三个性质的数集都可以进行dft运算

那么考虑为什么这个运算可以降低复杂度

首先将多项式奇偶分组

然后根据性质三

有：

此时发现我们通过mysterious transform 将问题范围缩小了一半

此时我们不考虑实现细节的分析复杂度

那么递归版的实现不难完成（待补

 

如果应用蝴蝶定理（玄学）

很快能写出又短又强的dft

void rev(int n,cpx*t){
    for(int i=0,j=0;i!=n;i++){
        if(i>j)swap(t[i],t[j]);
        for(int l=n/2;(j^=l)<l;l>>=1);
    }
}
void dft(int n,cpx*x,cpx*w){
    rev(n,x);
    for(int i=2;i<=n;i<<=1){
        int m=i/2;
        for(int j=0;j<n;j+=i){
            for(int k=0;k!=m;k++){
                cpx t=x[j+m+k]*w[n/i*k];
                x[j+m+k]=x[j+k]-t;
                x[j+k]=x[j+k]+t;
            }
        }
    }
}

其中cpx如下

struct cpx {
    double r,i;
    cpx(double real=0.0,double image=0.0) {
        r=real;i=image;
    }
    cpx operator +(const cpx w) {
        return cpx(r+w.r,i+w.i);
    }
    cpx operator -(const cpx w) {
        return cpx(r-w.r,i-w.i);
    }
    cpx operator *(const cpx w) {
        return cpx(r*w.r-i*w.i,r*w.i+i*w.r);
    }
};

IDFT

将点值转化为系数？

将单位根换成他的共轭复数

多项式乘法

如下

#include<map>
#include<stack>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<complex>
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;
#define inf 1001001001
#define infll 1001001001001001001LL
#define ll long long
#define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl
#define gmax(a,b) (a)=max((a),(b))
#define gmin(a,b) (a)=min((a),(b))
#define Ri register int
#define gc getchar()
#define il inline
il int read(){
    bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x;
}
#define gi read()
#define ig read()
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#define N 888888
struct cpx {
    double r,i;
    cpx(double real=0.0,double image=0.0) {
        r=real;i=image;
    }
    cpx operator +(const cpx w) {
        return cpx(r+w.r,i+w.i);
    }
    cpx operator -(const cpx w) {
        return cpx(r-w.r,i-w.i);
    }
    cpx operator *(const cpx w) {
        return cpx(r*w.r-i*w.i,r*w.i+i*w.r);
    }
};
cpx a[N],b[N];
cpx epsilon[N],arti_epsilon[N];
void init_epsilon(int n){
    double pi=acos(-1);
    for(int i=0;i!=n;i++){
        epsilon[i]=cpx(cos(2.0*pi*i/n),sin(2.0*pi*i/n)); 
        //arti_epsilon[i]=conj(epsilon[i]);
        arti_epsilon[i]=cpx(cos(2.0*pi*i/n),-sin(2.0*pi*i/n));
    }
}
void rev(int n,cpx*t){
    for(int i=0,j=0;i!=n;i++){
        if(i>j)swap(t[i],t[j]);
        for(int l=n/2;(j^=l)<l;l>>=1);
    }
}
void dft(int n,cpx*x,cpx*w){
    rev(n,x);
    for(int i=2;i<=n;i<<=1){
        int m=i/2;
        for(int j=0;j<n;j+=i){
            for(int k=0;k!=m;k++){
                cpx t=x[j+m+k]*w[n/i*k];
                x[j+m+k]=x[j+k]-t;
                x[j+k]=x[j+k]+t;
            }
        }
    }
}
cpx c[N]; 
void mul(cpx *a,cpx *b){
    int A,B;
    A=gi;B=gi;++A,++B;
    for(int i=0;i<A;i++)a[i].r=gi;
    for(int i=0;i<B;i++)b[i].r=gi;
    int t=max(A,B);
    int n=1;
    for(;n<t*2;n<<=1);
    init_epsilon(n);
    dft(n,a,epsilon);
    dft(n,b,epsilon);
    // py trade
    for(int i=0;i<n;i++)c[i]=a[i]*b[i];
    int nn=n;cout<<n;
    dft(n,c,arti_epsilon);
    for(int i=0;i<=A+B-1;i++)printf("%d ",(int)(c[i].r/nn+0.5));
}
int main(){
    mul(a,b);
    return 0;
}

UOJ34

模板测试

FNT

考虑double运算带来的运算偏差，我们采用另一种方式-原根

原根显然满足上面的性质

（原根 http://tonyfang.is-programmer.com/posts/205326.html

那么我们在取多个质数在该模意义下做DFT，就叫做FNT

最后答案通过CRT（中国剩余定理）来合并