万丈高楼平地起;勿在浮沙筑高台。
暂时放下其他的东西的学习,还不能称之为学习。潜心研究pbrt,看到第二章绕任意轴的旋转一部分,但是只是给了一个大体的推导,最终的推导并没有给出,所以在此做一下简单的推导。
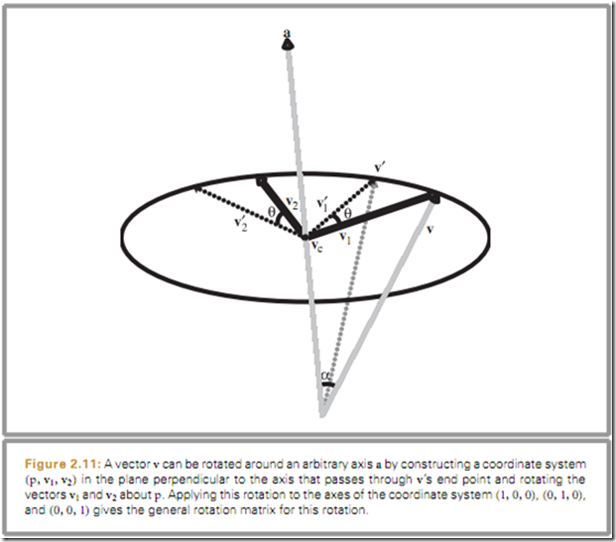
给定一个规范化的方向向量a作为旋转轴,然后使向量v绕着这个轴旋转θ度,如图1所示,首先我们计算一个平行于向量a的向量 ,此向量与向量a的起点相同,终点与向量v的终点(此时向量v与向量a起点相同)在以a为法线的平面上。假设向量v与a之间的夹角为 ,那么我们有
我们首先在这个平面上构造一组向量基 v1与 v2,其中 v1是v1=v - vc,
另外一个基向量可以通过两个向量的叉乘得到:v2 = (v1 x a),因为向量a是规范化的,所以v1与v2具有相同的长度,这个长度与v与vc之间的向量长度相同。在旋转平面(v1与v2所在的平面)来计算v绕向量vc旋转θ得到:
再继续下面推导之前先复习一下向量点乘与叉乘的基本规律:
向量点乘符合以下规律:
向量叉乘符合以下规律:
现在可以开始推导上面的公式了,推导过程如下:(手机效果太烂。。。将就着看吧)
最后附上源码:
1: Transform Rotate(float angle, const Vector &axis) {2: Vector a = Normalize(axis);3: float s = sinf(Radians(angle));4: float c = cosf(Radians(angle));5: float m[4][4];6:7: m[0][0] = a.x * a.x + (1.f - a.x * a.x) * c;8: m[0][1] = a.x * a.y * (1.f - c) - a.z * s;9: m[0][2] = a.x * a.z * (1.f - c) + a.y * s;10: m[0][3] = 0;11:12: m[1][0] = a.x * a.y * (1.f - c) + a.z * s;13: m[1][1] = a.y * a.y + (1.f - a.y * a.y) * c;14: m[1][2] = a.y * a.z * (1.f - c) - a.x * s;15: m[1][3] = 0;16:17: m[2][0] = a.x * a.z * (1.f - c) - a.y * s;18: m[2][1] = a.y * a.z * (1.f - c) + a.x * s;19: m[2][2] = a.z * a.z + (1.f - a.z * a.z) * c;20: m[2][3] = 0;21:22: m[3][0] = 0;23: m[3][1] = 0;24: m[3][2] = 0;25: m[3][3] = 1;26:27: Matrix4x4 mat(m);28: return Transform(mat, Transpose(mat));29: }


![]TM145XK7I`FRL`D[$8N3TC ]TM145XK7I`FRL`D[$8N3TC](https://images.cnblogs.com/cnblogs_com/cg_ghost/201204/201204271254237853.jpg)
![`9P5MH}21~V$U]83E1WL1{T `9P5MH}21~V$U]83E1WL1{T](https://images.cnblogs.com/cnblogs_com/cg_ghost/201204/201204271254287858.jpg)

![_L2@P]1C9`@8HBKU$UR958M _L2@P]1C9`@8HBKU$UR958M](https://images.cnblogs.com/cnblogs_com/cg_ghost/201204/201204271254311776.jpg)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号