一种高精度低复杂度的非线性函数定点计算方法

 摘要 在嵌入式系统中，由于没有浮点运算单元，当涉及浮点运算的时候需要做定点化处理。查表法是一种常用的方法。表的大小直接关系到计算的精度和复杂度。如何在计算精度和复杂度之间取得平衡，是一个重要的问题。本文根据泰勒公式重新设计了一种新的计算方法。这种方法具有很高的精度，而计算复杂度低，表的大小也很小。

 

引言

在多媒体数字信号处理中，经常要涉及一些非线性函数的计算。例如求开方，非整数幂次运算，对数运算，三角函数的计算等。嵌入式系统中的C编译器虽然提供了相应的库函数，但是在计算密集的地方要实时实现是比较困难的。查表法是一种常用的优化方法。采用这种方法必须根据自变量的范围和精度事先制作一张查找表。显然，输入的范围越大，精度要求越高，则所需的表格越大，需要的存储空间越大。查表法所需的计算就是根据输入值确定表的地址，根据表的地址就可以得到相应的函数值，因而运算量小。查表法比较适合非线性函数是周期函数或已知非线性函数的输入的动态变化范围的情况。本文以对数函数的计算为例阐述计算的过程。

浮点数的规格化

查表法比较适合于周期函数或自变量的动态范围比较小的场合。对于像对数函数Log2这样的非线性函数，输入自变量为任意一个大于0的实数，输出为任意实数。输入和输出的变化范围都很大，直接做表就很困难。有没有一种好的方法来解决表的大小的问题呢？浮点数的规格化方法为我们提供了一种好的思路。

对于任意一个实数x, 根据浮点数的规格化方法，可以把它写成下面的表达式：

      x = a * 2^m

 其中， a 是介于[0.5，1.0]之间的一个纯小数，而m 是一个整数。则求对数可以写成：

      log2(x) = log2(a * 2 ^m) = m + log2(a)

于是，求x的对数，实际上只要求解a的对数就可以了。而a的取值范围为[0.5，1.0].

         如何求得m呢？在嵌入式平台上，一般都有特殊的指令来求解这个值。例如，在TMS320C2X/5X中有一条专门的指令NORM用来对ACC寄存器中的数进行规格书，而在ARM上，ARMV5指令集中有一条CLZ指令来求前导零计数。

查找表

         由于a的取值范围在[0.5，1.0]之间,因此在[-1.0，0.0]之间。输入和输出均可以用Q15的顶点格式表示。可以对a的范围进行均匀划分，每一段的对数值都取每个小区间的左端点的值，这样就可以制作一张查找表。

          下表是把区间[0.5，1.0]均分为10个小区间生成的查找表。

 

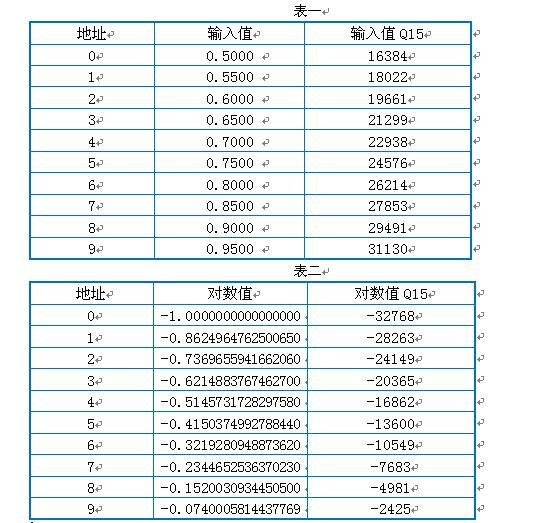
查表的地址计算如下：

例如输入为0.877,Q15的定点格式为0.877*2^15 = 28738.

表的地址： Index = ((28738 – 0.5 * 32768)/ (0.5/10))>>15 = 7.

于是，查表所得的对数值为上述第二个表的第7个值，即 -7683.

 

提高查表精度

         提高查表精度的一种简单的方法是采用线性插值的方法。既当计算所得的浮点index不是一个整数的时候，采用线性逼近的方法。而本文采取的方法是用泰勒公式展开的方法，可有效提高计算精度。本文采用下面的泰勒公式展开：

 

泰勒展开式中的2阶项分母里面的2也可以放到导数里面直接计算。x0是与查表地址相对应的输入变量值。这样，把它们做成表格如下：

 

 

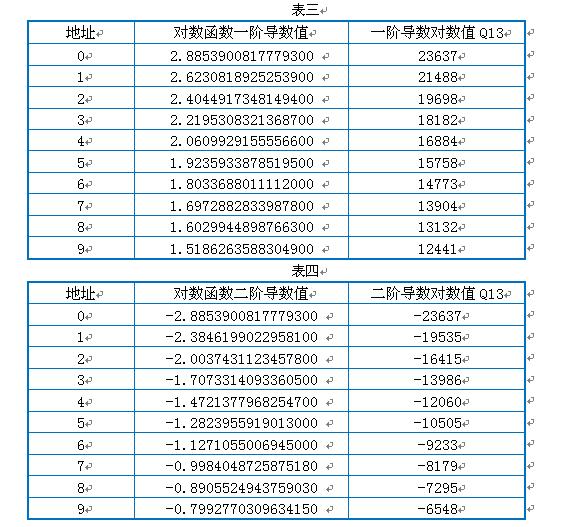
仍以上面的输入为例：

0.877,Q15的定点格式为0.877*2^15 = 28738

查表所得的index地址为第7个值，即 -7683.

泰勒公式表达式中： x – x0 = 28738 – 27853 = 885

经过一阶导数计算值： ((x – x0) * 13904)>>13 = 1502;

经过二阶导数的计算值：((((x-x0)*(x-x0))>>15)*(-8179))>>13 = -23;

 

综上，直接查表得到的对数值为：-7683

加上一阶导数的查表计算值为：-7683+1502 = -6181；

加上二阶导数的查表计算值为：-6181+ (-23)= -6204；

 

直接浮点计算的精确值Log2(0.877) = -0.189351252217354

查一次表计算所得浮点值-7683/32768 = -0.234466552734375

查一阶导数表计算所得浮点数值-6181/32768 = - 0.188629150390625

查二阶导数表计算所得浮点数值-6204/32768 = -0.1893310546875

 

由此可见，经过二阶导数查表计算所得的结果精度已经很高了，而计算只需3个乘法。

 

再举一例：求解Log2(10000)

分析与解答：输入是一个很大的正整数。首先求解出指数部分。

                  

于是，只需要求解0.610351525的对数即可。0.610351525的Q15格式为

0.610351525*2^15 = 20000

 

计算index地址为 (（20000-0.5*2^15）* 20 )>>15 = 2;

直接查表得到的对数值为：-24149

加上一阶导数的查表计算值为：-24149+815 = -23334；

加上二阶导数的查表计算值为：-23334+ (-7)= -23341；

 

而Log2(0.610351525)的直接浮点运算值为-0.712287709，Q15的定点表示为

-0.712287709*2^15 = 23340.24365,与上述二阶导数查表计算的定点格式相等。

结语

      

本文所述的方法具有运算精度高，查表表格小的特点，计算复杂度低的特点。非常适合于在嵌入式设备上实现。

本文所阐述的方法，不仅仅适用于以2为底数的对数的计算，也适合任意底对数的计算。同时，也非常适合计算其它一大类非线性函数。例如，开方运算，非整数幂次运算等。不管哪种运算，都只需要4个表格，每个表格10个16位数的数据量，计算只需要3个乘法和3个加法和表格的加载操作。

 

注：本文系作者多年之前的一篇论文改编。