支持向量机(Support Vector Machine)-----SVM之SMO算法(转)

此文转自两篇博文有修改

序列最小优化算法（英语：Sequential minimal optimization, SMO）是一种用于解决支持向量机训练过程中所产生优化问题的算法。SMO由微软研究院的约翰·普莱特（John Platt）发明于1998年，目前被广泛使用于SVM的训练过程中，并在通行的SVM库libsvm中得到实现。

1998年，SMO算法发表在SVM研究领域内引起了轰动，因为先前可用的SVM训练方法必须使用复杂的方法，并需要昂贵的第三方二次规划工具。而SMO算法较好地避免了这一问题。

前面最后留下来一个对偶函数最后的优化问题，原式为：

$max \quad \quad W(\alpha)=\sum\limits_{i=1}^{n}\alpha-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j))$

-----------------这个是由拉格朗日方法然后求偏导列式带入核函数得到的目标函数

$s.t.$ $\sum\limits_{i=1}^{n}y_i\alpha_i=0$

$0 \leq \alpha_i \leq C$

SMO就是要解这个凸二次规划问题，这里的C是个很重要的参数，它从本质上说是用来折中经验风险和置信风险的，C越大，置信风险越大，经验风险越小；并且所有的 $\alpha$ 因子都被限制在了以C为边长的大盒子里。

算法详述

(1)、 KKT条件

SMO是以C-SVC的KKT条件为基础进行后续操作的，这个KKT条件是：

$\alpha_i=0 \Leftrightarrow y_iu_i \geq 1$

$0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$

$\alpha_i=C \Leftrightarrow y_iu_i \leq 1$

其中 $u_i=<w,x_i>+b$

上述条件其实就是KT互补条件，SVM学习——软间隔优化一文，有如下结论：

$\alpha_i(y_i(<w,x_i />+b)- 1+\xi_i)=0$ $(i=1,2,...n)$

$\mu_i\xi_i=(\alpha_i-C)\xi_i=0$ $(i=1,2,...n)$

从上面式子可以得到的信息是：当 $\alpha_i=C$ 时，松弛变量 $\xi_i \geq 0$ ，此时有： $y_i(<w,x_i />+b)= 1-\xi_i \Rightarrow y_i(<w,x_i>+b) \leq 1 \Rightarrow y_iu_i \leq 1$ ，对应样本点就是误分点；当 $\alpha_i=0$ 时，松弛变量 $\xi_i$ 为零，此时有 $y_i(<w,x_i />+b) \geq 1 \Rightarrow y_iu_i \geq 1$ ，对应样本点就是内部点，即分类正确而又远离最大间隔分类超平面的那些样本点；而 $0 < \alpha_i <C$ 时，松弛变量 $\xi_i$ 为零，有 $y_i(<w,x_i />+b) = 1 \Rightarrow y_iu_i = 1$ ，对应样本点就是支持向量。

(2)、凸优化问题停止条件

对于凸优化问题，在实现时总需要适当的停止条件来结束优化过程，停止条件可以是：

1、监视目标函数 $W(\alpha)$ 的增长率，在它低于某个容忍值时停止训练，这个条件是最直白和简单的，但是效果不好；

2、监视原问题的KKT条件，对于凸优化来说它们是收敛的充要条件，但是由于KKT条件本身是比较苛刻的，所以也需要设定一个容忍值，即所有样本在容忍值范围内满足KKT条件则认为训练可以结束；

3、监视可行间隙，它是原始目标函数值和对偶目标函数值的间隙，对于凸二次优化来说这个间隙是零，以一阶范数软间隔为例：

原始目标函数 $O(w,b)$ 与对偶目标函数 $W(\alpha)$ 的差为：

$Gap=\frac{1}{2}<w,w />+C\sum\limits_{i=1}^{n}\xi_i-( \sum\limits_{i=1}^{n}\alpha-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j)))$

$=\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_jK(x_i,x_j)+C\sum\limits_{i=1}^{n}\xi_i-( \sum\limits_{i=1}^{n}\alpha_i-\frac{1}{2}\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_j(K(x_i,x_j)))$

$=\sum\limits_{i,j=1}^{n}{y_iy_j\alpha_i\alpha_jK(x_i,x_j)+C\sum\limits_{i=1}^{n}\xi_i- \sum\limits_{i=1}^{n}\alpha_i$

$=2 \sum\limits_{i=1}^{n}\alpha_i -2W(\alpha)+C\sum\limits_{i=1}^{n}\xi_i- \sum\limits_{i=1}^{n}\alpha_i$

$= \sum\limits_{i=1}^{n}\alpha_i -2W(\alpha)+C\sum\limits_{i=1}^{n}\xi_i$

定义比率：

$\frac{O(w,b)-W(\alpha)}{O(w,b)+1)}$ ，可以利用这个比率达到某个容忍值作为停止条件。

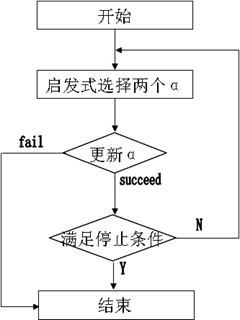
(3)、SMO思想

沿袭分解思想，固定“Chunking工作集”的大小为2，每次迭代只优化两个点的最小子集且可直接获得解析解，算法流程：

(4)、仅含两个Langrange乘子解析解

为了描述方便定义如下符号：

$K_{ij}=K(\mathbf{x_i}, \mathbf{x_j})$

$f(\mathbf{x_i})=\sum_{j=1}^n y_i \alpha_i K_{ij} + b$

$v_i=\sum_{j=3}^n y_j \alpha_j K_{ij} =f(\mathbf{x_i})-\sum_{j=1}^2 y_j \alpha_j K_{ij} - b$

于是目标函数就变成了：

$W(\alpha_2) =\sum_{i=1}^n \alpha_i - \frac12 \sum_{i=1}^n \sum_{j=1}^n y_i y_j K(x_i, x_j) \alpha_i \alpha_j \\$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^n(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^2(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$-\frac{1}{2}\sum_{i=3}^n(\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}+\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)})$

$=\alpha_1+\alpha_2+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=1}^2\sum_{j=1}^2y_iy_j\alpha_i\alpha_jK{(x_ix_j)}-\sum_{i=1}^2\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 \\$

$-y_1\alpha_1\sum_{j=3}^ny_j\alpha_jK{(x_1x_j)}-y_2\alpha_2\sum_{j=3}^ny_j\alpha_jK{(x_2x_j)}$

$+ \sum_{i=3}^n \alpha_i-\frac{1}{2}\sum_{i=3}^n\sum_{j=3}^ny_iy_j\alpha_i\alpha_jK{(x_ix_j)}$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 \\$

$- y_1 \alpha_1 v_1 - y_2 \alpha_2 v_2 + \text{constant} \$

注意第一个约束条件： $\sum_{i=1}^n y_i \alpha_i = 0$ ，可以将 $\alpha_3, \ldots, \alpha_n, y_3, \ldots, y_n$ 看作常数，有 $\alpha_1 y_1 + \alpha_2 y_2 = C^'$ ( $C^'$ 为常数，我们不关心它的值)，等式两边同时乘以 $y_1$ ，得到 $\alpha_1 = \gamma - s \alpha_2$ （ $\gamma$ 为常数，其值为 $C^'y_1$ ，我们不关心它，）。将 $\alpha_1$ 用上式替换则得到一个只含有变量 $\alpha_2$ 的求极值问题：

$W(\alpha_2) =\gamma - s \alpha_2 + \alpha_2 - \frac12 K_{11} (\gamma - s \alpha_2)^2 - \frac12 K_{22} \alpha_2^2 \\$

$- s K_{12} (\gamma - s \alpha_2)\alpha_2 - y_1(\gamma - s \alpha_2)v_1 - y_2 \alpha_2 v_2 + \text{constant}$

这下问题就简单了，对 $\alpha_2$ 求偏导数得到：

$\frac{\partial W(\alpha_2)}{\partial \alpha_2} = -s + 1 + s K_{11} \gamma - K_{11} \alpha_2 - K_{22}\alpha_2 -s\gamma K_{12}+ 2K_{12}\alpha_2 + y_2v_1 - y_2 v_2 = 0$

将 $y_2^2=1$ 、 $s=y_1y_2$ 带入上式有：

$\alpha_2^{new} = \frac{y_2(y_2 - y_1 + y_1 \gamma (K_{11}-K_{12})+v_1-v_2)}{K_{11}+K_{22}-2K_{12}}$

带入 $v_i$ 、 $\gamma =\alpha_1^{old} + s \alpha_2^{old}$ ，用 $E_i = f(\mathbf{x}_i) - y_i$ ，表示误差项(可以想象，即使分类正确， $f(x_i)$ 的值也可能很大)、 $\eta = K_{11}+K_{22}-2K_{12} \ = ||\Phi(x_1)-\Phi(x_2)||^2$ ( $\Phi$ 是原始空间向特征空间的映射)，这里 $\sqrt {\eta }$ 可以看成是一个度量两个样本相似性的距离，换句话说，一旦选择核函数则意味着你已经定义了输入空间中元素的相似性。

最后得到迭代式：

$\alpha_2^{new} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$

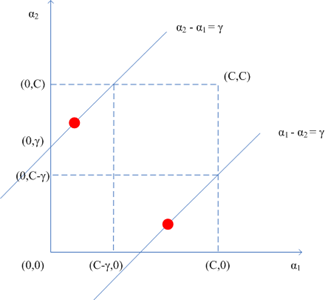
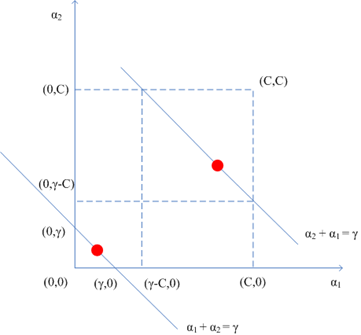
注意第二个约束条件——那个强大的盒子： $0 \leq \alpha_i \leq C$ ，这意味着 $\alpha_2^{new}$ 也必须落入这个盒子中，综合考虑两个约束条件，下图更直观：

$y_1$ 和 $y_2$ 异号的情形

$y_1$ 和 $y_2$ 同号的情形

可以看到 $\alpha_1, \alpha_2$ 两个乘子既要位于边长为C的盒子里又要在相应直线上，于是对于 $\alpha_2$ 的界来说，有如下情况：

$\begin{cases} \ L=max{\left\{0, \alpha_2^{old} - \alpha_1^{old}\right\}} \quad \quad \quad & y_1y_2 = -1, \\ \ L=max{\left\{0, \alpha_1^{old} + \alpha_2^{old} - C \right\}}& y_1y_2 = 1, \end{cases$ $\begin{cases} \ H=min{\left\{C, C + \alpha_2^{old} - \alpha_1^{old}\right\}} \quad \quad & y_1y_2 = -1\\ \ H=min{\left\{C, \alpha_1^{old} + \alpha_2^{old} \right\}}& y_1y_2 = 1 \end{cases}$

整理得下式：

$\alpha_2^{new,clipped} = \begin{cases} \ L \quad \quad \quad & \alpha_2^{new} \leq L\\ \ \alpha_2^{new} \quad \quad \quad & L< \alpha_2^{new} < H\\ \ H \quad & \alpha_2^{new} \geq H \end{cases}$

又因为 $\alpha_1^{old} = \gamma - s \alpha_2 ^{old}$ ， $\alpha_1^{new} = \gamma - s \alpha_2 ^{new,clipped}$ ，消去 $\gamma$ 后得到：

$\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new,clipped})$

(5).综上可总结出SMO的算法框架

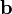SMO算法是一个迭代优化算法。在每一个迭代步骤中，算法首先选取两个待更新的向量，此后分别计算它们的误差项，并根据上述结果计算出和。最后再根据SVM的定义计算出偏移量 $\mathbf{b}$ 。对于误差项而言，可以根据、和b的增量进行调整，而无需每次重新计算。具体的算法如下：

1. 随机数初始化向量权重，并计算偏移b。(这一步初始化向量权重只要使符合上述的约束条件即可，原博文的程序就是range函数)

2.初始化误差项，其中

$E_i = f(\mathbf{x}_i) - y_i$

$f(\mathbf{x_i})=\sum_{j=1}^n y_i \alpha_i K_{ij} + b$

3.选取两个向量作为需要调整的点（例如第一次下标为1，2两点，第二次下标3，4...........），然后

令 $\alpha_2^{new} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$ 其中 $\eta = K_{11}+K_{22}-2K_{12} \ = ||\Phi(x_1)-\Phi(x_2)||^2$ ( $\Phi$ 是原始空间向特征空间的映射)， $K_{ij}=K(\mathbf{x_i}, \mathbf{x_j})$

4.if >H 令=H if <L 令=L （L，H前面已给出）

5.令

6.利用更新的和修改和b的值

7.如果达到终止条件，则算法停止，否则转向3

算法补充说明：

 优化向量选择方法

可以采用启发式的方法选择每次迭代中需要优化的向量。第一个向量可以选取不满足支持向量机KKT条件的向量，亦即不满足

即：

$\alpha_i=0 \Leftrightarrow y_iu_i \geq 1$

$0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$

$\alpha_i=C \Leftrightarrow y_iu_i \leq 1$ 其中 $u_i=<w,x_i>+b$

的向量。而第二个向量可以选择使得最大的向量。

终止条件

SMO算法的终止条件可以为KKT条件对所有向量均满足，或者目标函数增长率小于某个阈值，即

（根据前面的凸优化问题停止条件所说，此效果可能不佳，可选择其他方法,见(2))

---------------------------------以下内容是有关可行间隙方法，乘子优化，SMO加速问题，是深化的内容------------------------------------------------

(6)、启发式的选择方法

根据选择的停止条件可以确定怎么样选择点能对算法收敛贡献最大，例如使用监视可行间隙的方法，一个最直白的选择就是首先优化那些最违反KKT条件的点，所谓违反KKT条件是指：

$\alpha_i=0 \quad \quad \quad && \quad \quad \quad y_iu_i<1$

$0 \leq \alpha_i \leq C \quad \quad \quad && \quad \quad \quad y_iu_i \neq 1$

$\alpha_i=C \quad \quad \quad && \quad \quad \quad y_iu_i /> 1$

其中KKT条件

由前面的停止条件3可知，对可行间隙贡献最大的点是那些

$Gap_i=\alpha_i(y_i(\sum\limits_{j=1}^{n}\alpha_jy_iK(x_i,x_j))-1)+C\xi_i=\alpha_i(y_iu_i-1-y_ib))+C\xi_i$

其中， $\xi_i=max(0,1-y_iu_i)$

取值大的点，这些点导致可行间隙变大，因此应该首先优化它们(原因见原博文：http://www.cnblogs.com/vivounicorn/archive/2011/06/01/2067496.html)

SMO的启发式选择有两个策略：

启发式选择1：

最外层循环，首先，在所有样本中选择违反KKT条件的一个乘子作为最外层循环，用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化，接着，从所有非边界样本中选择违反KKT条件的一个乘子作为最外层循环，用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化(之所以选择非边界样本是为了提高找到违反KKT条件的点的机会)，最后，如果上述非边界样本中没有违反KKT条件的样本，则再从整个样本中去找，直到所有样本中没有需要改变的乘子或者满足其它停止条件为止。

启发式选择2：

内层循环的选择标准可以从下式看出：

$\alpha_2^{new} = \alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$

要加快第二个乘子的迭代速度，就要使 $\alpha_2^{old} + \frac{y_2(E_1-E_2)}{\eta}$ 最大，而在 $\eta$ 上没什么文章可做，于是只能使 $|E_1-E_2|$ 最大。

确定第二个乘子方法：

1、首先在非界乘子中寻找使得 $|E_1-E_2|$ 最大的样本；

2、如果1中没找到则从随机位置查找非界乘子样本；

3、如果2中也没找到，则从随机位置查找整个样本(包含界上和非界乘子)。

(7)、关于两乘子优化的说明

由式子

$\frac{\partial W(\alpha_2)}{\partial \alpha_2} = -s + 1 + s K_{11} \gamma - K_{11} \alpha_2 - K_{22}\alpha_2 -s\gamma K_{12}+ 2K_{12}\alpha_2 + y_2v_1 - y_2 v_2$

可知：

$\frac{\partial W^2(\alpha_2)}{\partial \alpha_2^2} = - K_{11} - K_{22}+ 2K_{12}=-\eta$

于是对于这个单变量二次函数而言,如果其二阶导数 $-\eta < 0$ ，则二次函数开口向下，可以用上述迭代的方法更新乘子，如果 $-\eta \geq 0$ ，则目标函数只能在边界上取得极值(此时二次函数开口向上)，换句话说，SMO要能处理 $\eta$ 取任何值的情况，于是在 $-\eta \geq 0$ 时有以下式子：

1、 $\alpha_2^{new,clipped}=L$ 时：

$\alpha_1^{new}= \alpha_1^{old}+s(\alpha_2^{old}-L)$

2、 $\alpha_2^{new,clipped}=H$ 时：

$\alpha_1^{new}= \alpha_1^{old}+s(\alpha_2^{old}-H)$

3、 $W(\alpha_1,\alpha_2) =\sum_{i=1}^n \alpha_i - \frac12 \sum_{i=1}^n \sum_{j=1}^n y_i y_j K(x_i, x_j) \alpha_i \alpha_j \\$

$=\alpha_1+\alpha_2-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 - y_1 \alpha_1 v_1 - y_2 \alpha_2 v_2 + \text{constant} \$

$=\alpha_1(1-y_1v_1)+\alpha_2(1-y_2v_2)-\frac12 K_{11} \alpha_1^2 - \frac12 K_{22} \alpha_2^2 - y_1 y_2 K_{12} \alpha_1 \alpha_2 + \text{constant} \$

$=\alpha_1y_1(y_1-(f(x_1)-\alpha_1y_1K_{11}-\alpha_2y_2K_{12}-b))+\alpha_2y_2(y_2-(f(x_2)-\alpha_1y_1K_{12}-\alpha_2y_2K_{22}-b))$

$=\alpha_1^{new}(y_1(b-E_1)+\alpha_1^{old}K_{11}+s\alpha_2^{old}K_{12})+ \alpha_2^{new,clipped}(y_2(b-E_2)+\alpha_2^{old}K_{22}+s\alpha_1^{old}K_{12})$

分别将乘子带入得到两种情况下的目标函数值： $W_L$ 和 $W_H$ 。显然，哪种情况下目标函数值最大，则乘子就往哪儿移动，如果目标函数的差在某个指定精度范围内，说明优化没有进展。

另外发现，每一步迭代都需要计算输出 $u$ 进而得到 $E$ ，于是还要更新阈值 $b$ ，使得新的乘子 $\alpha_1$ 、 $\alpha_2$ 满足KKT条件，考虑 $\alpha_1$ 、 $\alpha_2$ 至少有一个在界内，则需要满足 $0 \leq \alpha_i \leq C \Leftrightarrow y_iu_i = 1$ ，于是 $b$ 的迭代可以这样得到：

1、设 $\alpha_1 ^{new}$ 在界内，则：

$y_1u_1^{new}=1 \Rightarrow y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{new})=1$

又因为：

$E_1=\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{old}-y_1$ $\Rightarrow \sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})=E_1-\alpha_1^{old}y_1K_{11}-\alpha_2^{old}y_2K_{21}-b^{old}+y_1$

于是有：

$y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+\sum \limit_{i=3}^{n}(\alpha_iy_iK_{i1})+b^{new})$

$=y_1(\alpha_1^{new}y_1K_{11}+\alpha_2^{new,clipped}y_2K_{21}+E_1-\alpha_1^{old}y_1K_{11}-\alpha_2^{old}y_2K_{21}-b^{old}+y_1+b^{new})= 1$

等式两边同乘 $y_1$ 后移项得：

$b^{new}=-\alpha_1^{new}y_1K_{11}-\alpha_2^{new,clipped}y_2K_{21}-E_1+\alpha_1^{old}y_1K_{11}+\alpha_2^{old}y_2K_{21}+b^{old}$

$=(\alpha_1^{old}-\alpha_1^{new})y_1K_{11}+(\alpha_2^{old}-\alpha_2^{new,clipped})y_2K_{21}-E_1+b^{old}$ ；

2、设 $\alpha_2^{new,clipped}$ 在界内，则：

$b^{new} =(\alpha_1^{old}-\alpha_1^{new})y_1K_{12}+(\alpha_2^{old}-\alpha_2^{new,clipped})y_2K_{22}-E_2+b^{old}$ ；

3、设 $\alpha_1 ^{new}$ 、 $\alpha_2^{new,clipped}$ 都在界内，则：情况1和情况2的 $b$ 值相等，任取一个；

4、设 $\alpha_1 ^{new}$ 、 $\alpha_2^{new,clipped}$ 都不在界内，则： $b^{new}$ 取值为情况1和情况2之间的任意值。

(8)、提高SMO的速度

从实现上来说，对于标准的SMO能提高速度的地方有：

1、能用缓存的地方尽量用，例如，缓存核矩阵，减少重复计算，但是增加了空间复杂度；

2、如果SVM的核为线性核时候，可直接更新 $w$ ，毕竟每次计算 $w=\sum\limits_{i=1}^n y_i\alpha_ix_i$ 的代价较高，于是可以利用旧的乘子信息来更新 $w$ ，具体如下：

$w^{new}=w^{old}+(\alpha_1^{new}-\alpha_1^{old})y_1x_1 +(\alpha_2^{new}-\alpha_2^{old})y_2x_2$ ，应用到这个性质的例子可以参见SVM学习——Coordinate Desent Method。

3、关注可以并行的点，用并行方法来改进，例如可以使用MPI，将样本分为若干份，在查找 $|E_1-E_2|$ 最大的乘子时可以现在各个节点先找到局部最大点，然后再从中找到全局最大点；又如停止条件是监视对偶间隙，那么可以考虑在每个节点上计算出局部可行间隙，最后在master节点上将局部可行间隙累加得到全局可行间隙。

posted on 2012-07-17 12:49 as_ 阅读(24880) 评论(1) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

华山大师兄