poj 1988 Cube Stacking
poj 1988 Cube Stacking
http://poj.org/problem?id=1988
Description
Farmer John and Betsy are playing a game with N (1 <= N <= 30,000)identical cubes labeled 1 through N. They start with N stacks, each containing a single cube. Farmer John asks Betsy to perform P (1<= P <= 100,000) operation. There are two types of operations:
moves and counts.
* In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
* In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.
Write a program that can verify the results of the game.
moves and counts.
* In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
* In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.
Write a program that can verify the results of the game.
Input
* Line 1: A single integer, P
* Lines 2..P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a 'M' for a move operation or a 'C' for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.
Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.
* Lines 2..P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a 'M' for a move operation or a 'C' for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.
Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.
Output
Print the output from each of the count operations in the same order as the input file.
Sample Input
6 M 1 6 C 1 M 2 4 M 2 6 C 3 C 4
Sample Output
1 0 2
题目大意:
有块积木,开始时它们都属于不同的集合。
然后输入p,表示有p个操作。每个操作都有一个t,如果t==M,那么输入x,y,把x所在集合的所有积木,都堆到y所在集合的上面;如果t==C,那么输入x,查询并输出x下面有多少个积木(不包括x本身)。
解题思路:加权并查集
先设2个数组,under[i]=j表示在积木i下面有j个积木;tot[i]=j表示i所在集合一共有j个积木。

由此可以看出,如果我们要把x摞到y的上面,
在合并操作时,x的下面多了y所在集合的全体,所以under[x]=under[x]+tot[y];x的father指向y,y所代表的集合总数多了x所在集合的全体,所以tot[y]=tot[x]+tot[y]
上面还更新了tot[x]=0,这个在代码中更不更新无所谓,并查集合并操作合并祖先节点,x的father指向了y,x不会再作为祖先节点出现
在查询祖先节点时,我们需要维护under[]
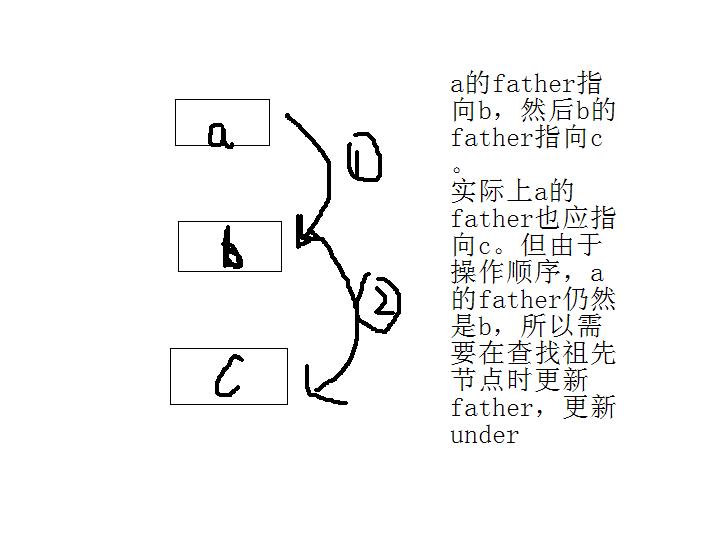
在路径压缩中更新under时,要先记录下i的祖先节点,在递归回溯时先加上i原父节点的under,再把i的父节点更新为祖先节点。
#include<cstdio> #include<iostream> using namespace std; int p,father_x,father_y; char c; int x,y,un; int under[30001],tot[30001],fa[30001];//under:下面有几个积木 tot:集合一共有几个积木 int find(int i) { //先更新under再路径压缩 if(fa[i]!=i) { int tmp=find(fa[i]); under[i]+=under[fa[i]]; fa[i]=tmp; } return fa[i]; } void unionn()//x摞到y的上面 { under[father_x]+=tot[father_y]; tot[father_y]+=tot[father_x]; fa[father_x]=father_y; } int main() { scanf("%d",&p); for(int i=0;i<=30000;i++) tot[i]=1,fa[i]=i; while(p--) { cin>>c; if(c=='M') { scanf("%d%d",&x,&y); father_y=find(y); father_x=find(x); if(father_x!=father_y) unionn(); } else { scanf("%d",&x); find(x); printf("%d\n",under[x]); } } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号