〖算法〗-- 快速排序 、希尔排序、计数排序

【快速排序 、希尔排序、计数排序】

快速排序 quick sort

介绍：
　　快速排序（Quicksort）是对冒泡排序的一种改进。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n²)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

原理：

　　通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行，以此达到整个数据变成有序序列，最终完成整个数据排序的目的。 值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

步骤：
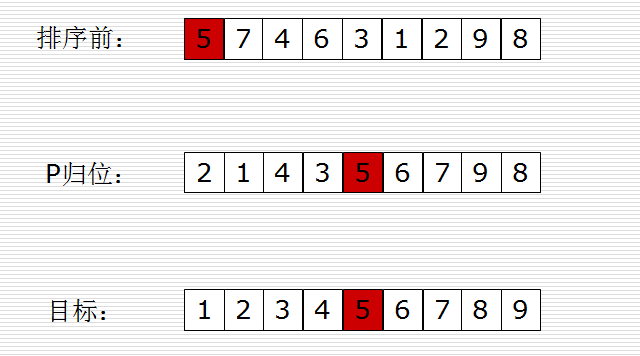
　　1、从数列中挑出一个元素，称为 “基准”（pivot），
　　2、重新排序数列，将基准归位！所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
　　3、递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

　　注：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。要注意的是，排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。 

革新点：先从后扫描(比基准值)小的，再从前扫描(比基准值)大的！

快速排序动画演示：

算法实现：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

import random as rd import time import sys   sys.setrecursionlimit(100000)   def cal_time(func):     """     装饰器打印执行时间     """     def wrapper(*args, **kwargs):         t1 = time.time()         x = func(*args, **kwargs)         t2 = time.time()         print("%s running time %s secs." % (func.__name__, t2 - t1))         return x               return wrapper   def partition(data, left, right):     """     区内数据排序处理     快速排序的核心代码。     其实就是将选取的tmp不断交换，将比它小的换到左边，将比它大的换到右边。     它自己也在交换中不断变换自己的位置，直到完成所有的交换为止。     但在函数调用的过程中，pivot_key的值始终不变。     :param low:左边界索引     :param high:右边界索引     :return:分完左右区后tmp所在位置的索引     """     tmp = data[left]     while left < right:         while left < right and data[right]>=tmp:             right-=1         data[left]=data[right]         while left < right and data[left]<=tmp:             left+=1         data[right]=data[left]     data[left]=tmp     return left       def _quick_sort(data, left, right):     """     递归调用     """     if left < right:         mid = partition(data, left, right)         _quick_sort(data, left, mid - 1)         _quick_sort(data, mid + 1, right)   @cal_time def quick_sort(data):     """     调用入口     """     return _quick_sort(data, 0, len(data)-1)       li = list(range(100000)) rd.shuffle(li) quick_sort(li)

总结：

• 快速排序的时间性能取决于递归的深度。
• 当tmp恰好处于记录关键码的中间值时，大小两区的划分比较均衡，接近一个平衡二叉树，此时的时间复杂度为O(nlog(n))。
• 当原记录集合是一个正序或逆序的情况下，分区的结果就是一棵斜树，其深度为n-1，每一次执行大小分区，都要使用n-i次比较，其最终时间复杂度为O(n^2)。
• 在一般情况下，通过数学归纳法可证明，快速排序的时间复杂度为O(nlog(n))。
• 但是由于关键字的比较和交换是跳跃式的，因此，快速排序是一种不稳定排序。
• 同时由于采用的递归技术，该算法需要一定的辅助空间，其空间复杂度为O(logn)。

希尔排序 Shell Sort

介绍：

　　希尔排序（Shell Sort）也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。
　　该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高。

执行流程：
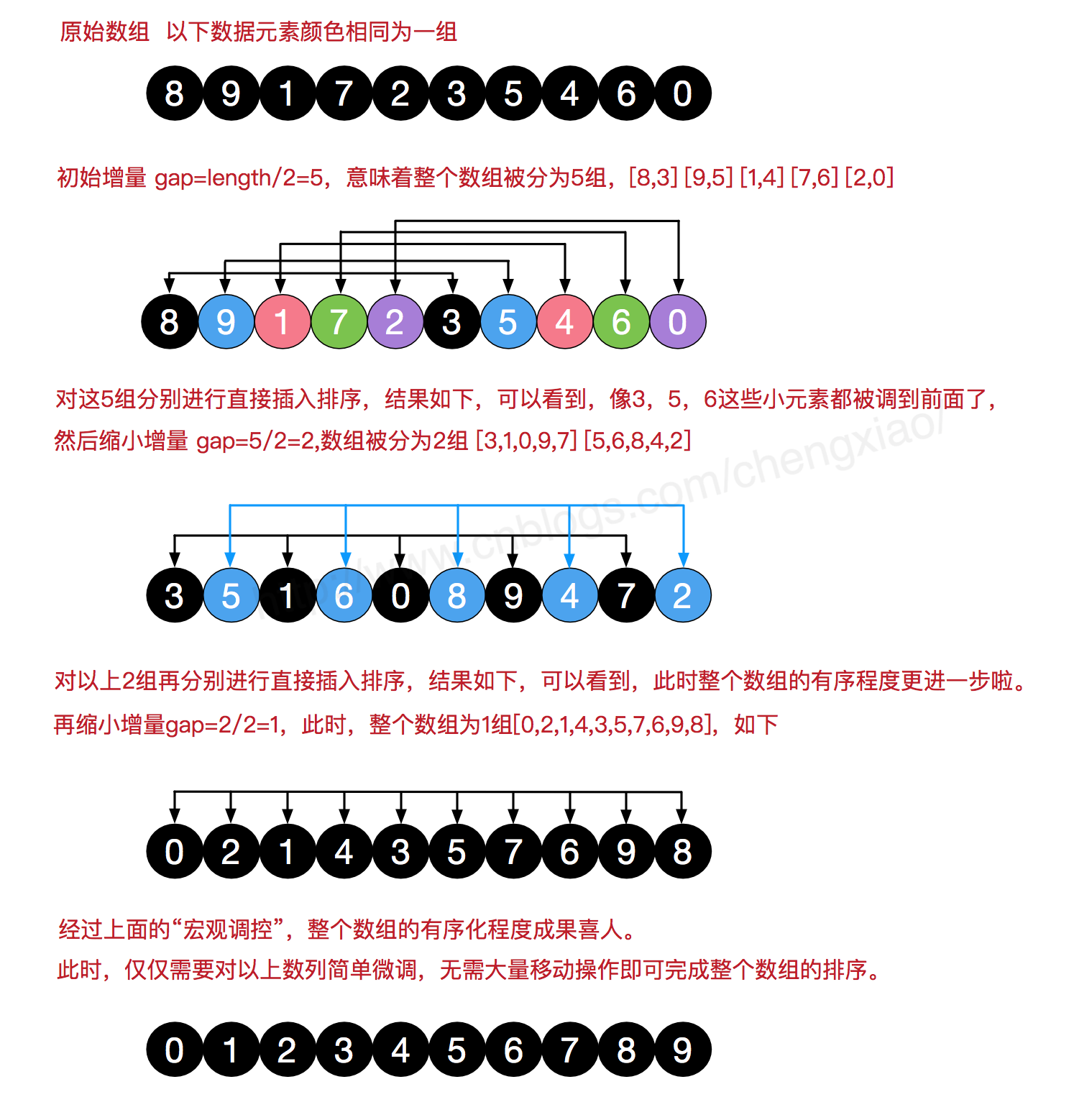
　　首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1[一组内数据间隔是d1构成的分组]，在各组内进行直接插入排序；
　　取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。
　　通常每一次分组间隔都是上一次分组的一半，直到最后为1直接执行插入排序！

举例：

　　我们来看下希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2...1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

希尔排序动态展示：

算法实现：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

def shell_sort(li):     """     希尔算法 分组插入算法，逐渐有序     :param li: 无序列表     :return: 有序列表     """     gap = len(li) // 2 #初始分组间隔     while gap > 0:         #组内排序         # 以0~(gap-1)位的数作为各自分组的第一个数         for i in range(gap, len(li)): #从gap位开始与自己组内数据比较             tmp = li[i] #获取当前位置的值             j = i - gap #自己所在分组，间隔为gap的值             while j >= 0 and tmp < li[j]: #比较，如果当前值比前一个值小                 li[j + gap] = li[j] #把大的值赋给当前位置                 j -= gap #再去当前组内间隔为gap的值比较             li[j + gap] = tmp #否则的话就不变         #当前分组内值比较完成         gap = gap // 2 #间隔减半，组内再排序       return li

总结：
　　希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。
　　希尔排序是一种分组插入排序算法。将原数据集合分割成若干个子序列，然后再对子序列分别进行直接插入排序，使子序列基本有序，最后再对全体记录进行一次直接插入排序。
　　最关键的是跳跃和分割的策略，也就是我们要怎么分割数据，间隔多大的问题。通常将相距某个“增量”的记录组成一个子序列，这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。

希尔排序的时间复杂度为： O(1.3n)

参考博客：常用排序算法总结(二)

计数排序 counting sort

　　1.计数排序是一种非常快捷的稳定性强的排序方法，时间复杂度O(n+k),其中n为要排序的数的个数，k为要排序的数的组大值。计数排序对一定量的整数排序时候的速度非常快，一般快于其他排序算法。但计数排序局限性比较大，只限于对整数进行排序。计数排序是消耗空间发杂度来获取快捷的排序方法，其空间发展度为O（K）同理K为要排序的最大值。

　　2.计数排序的基本思想为一组数在排序之前先统计这组数中其他数小于这个数的个数，则可以确定这个数的位置。例如要排序的数为 7 4 2 1 5 3 1 5；则比7小的有7个数，所有7应该在排序好的数列的第八位，同理3在第四位，对于重复的数字，1在1位和2位（暂且认为第一个1比第二个1小），5和1一样位于6位和7位。 

计数排序非常基础，他的主要目的是对整数排序并且会比普通的排序算法性能更好。例如，输入{1, 3, 5, 2, 1, 4}给计数排序，会输出{1, 1, 2, 3, 4, 5}。这个算法由以下步骤组成：

　　初始化一个计数数组，大小是输入数组中的最大的数。
　　遍历输入数组，遇到一个数就在计数数组对应的位置上加一。例如：遇到5，就将计数数组第五个位置的数加一。
　　把计数数组直接覆盖到输出数组（节约空间）。

时间复杂度：O(n)

统计一个列表内每个元素出现的个数。用于小规模范围内计算！

弊端：

　　有限定！为排序需要新建一个列表，开辟一块内存空间，而且这个空间的大小取决于排序列表的最大值。

　　如果一个要排序的列表中仅有，【1，10000】这两个数，那么我们统计的话，创建的用于计数的列表就要开一一个可以存放10000个数的内存空间。这样导致的结果就是，其他的数无用并且损耗性能，时间复杂度没变但是空间复杂度增加了！这也间接的暴露了范围取值的弊端。

算法实现：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

def count_sort(li, maxnum=100):     """     新建一个列表，往列表内写值     :param li:     :param maxnum:     :return:     """     count = [0 for i in range(maxnum+1)]  #创建用以计数的所有元素都是0的列表，     result = []     for i in li: #遍历要计数的列表，每个元素对应的索引位置的数加1         count[i] += 1     for num, count in enumerate(count): #对已经完成计数的列表进行枚举打印,格式(数字，次数)         for i in range(count): #再通过次数创建一个循环，出现多少次就把对应的数写入列表多少次             result.append(num)   def count_sorts(li, max_num):     """     仅在当前列表下操作，按照次数重写列表     :param li:     :param max_num:     :return:     """     count = [0 for i in range(max_num + 1)]     for num in li:         count[num] += 1     i = 0     for num,m in enumerate(count):         for j in range(m):             li[i] = num             i += 1     return li   li = [3,4,1,2,5,6,6,5,4,3,3] print(count_sorts(li,max(li)))

应用：

　　有一个数组[3,4,1,2,5,6,6,5,4,3,3]请写一个函数，找出该数组中没有重复的数的总和（上面的没有重复数的总和为 1+2=3）。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

def count_sorts(li, max_num):     """     计数排序引申，求和     :param li: 传入的列表     :param max_num:列表中最大值     :return:和 sums     """     counts = [0 for i in range(max_num + 1)]     for num in li:         counts[num] += 1     sums = 0     for num,count in enumerate(counts):         # print(num,count) #打印列表内对应数字出现的次数         if count == 1:             sums += num     return sums   li = [3,4,1,2,5,6,6,5,4,3,3] print(count_sorts(li,max(li)))