为什么点积等价于投影后的乘积
为什么点积等价于投影后的乘积
先上结论:
-
\(\boldsymbol v\)和\(\boldsymbol w\)点积,就是向量乘法\(\boldsymbol v × \boldsymbol w^T\);
-
\(\boldsymbol w\)象征着一个降维变换矩阵,因此该矩阵乘法本质上是一个\(\boldsymbol v\)降维的过程;
-
该降维变换在几何上正是投影过程。
综上,点积的几何意义就是投影相乘。
摘自《Essence of linear algebra》系列视频,非常精彩。B站上有全集~
要理解这一点,需要线性代数基础,要理解矩阵和变换之间的关系。
1. 复习点积
我们所学的向量点积是这样的:
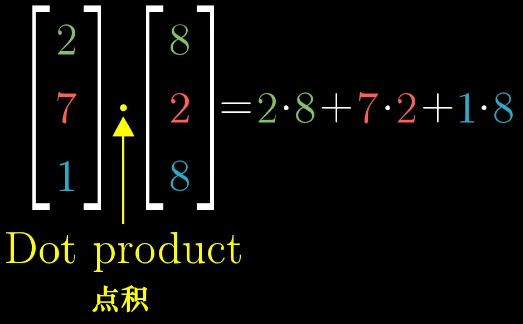
其几何解释为:向量\(\boldsymbol w\)在向量\(\boldsymbol v\)上投影,投影长度和\(|\boldsymbol v|\)相乘。

借助这一几何解释,我们可以直观地理解:
-
向量正交:点积为0
-
投影为反方向:点积为负。
2. 点积的对称性
注意!理解、证明点积的对称性,对我们的证明至关重要!
假设\(\boldsymbol w \bigodot \boldsymbol v\),对称性的意思是:
无论是\(\boldsymbol v\)在\(\boldsymbol w\)上作投影再乘,还是\(\boldsymbol w\)在\(\boldsymbol v\)上作投影再乘,结果都是一样的。
现在我们证明这一点。
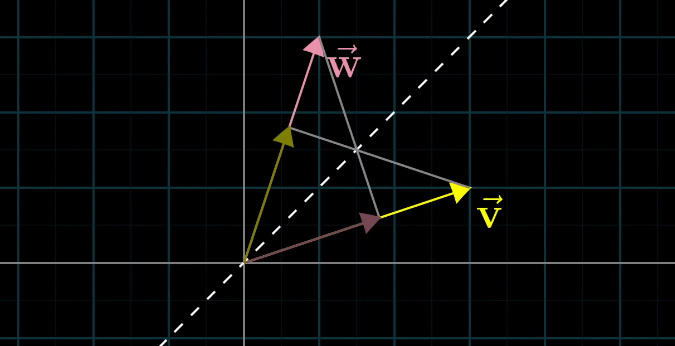
如图,假设二者长度相同,那么对称性显然成立:因为投影长度是一样的。
现在,假设\(\boldsymbol w\)更长。
我们在\(\boldsymbol w\)的方向上取\(\boldsymbol w'\),使得\(|\boldsymbol w'|\)等于\(|\boldsymbol v|\)。
我们先考虑\(\boldsymbol w' \bigodot \boldsymbol v\)。由于长度相同,对称性是显然的。
而\(\boldsymbol w \bigodot \boldsymbol v\),和\(\boldsymbol w' \bigodot \boldsymbol v\)只相差常数\(\alpha\)倍:
3. 矩阵与变换的关系
这一节内容,强烈建议观看推荐视频:《Essence of linear algebra》。
假设现在有矩阵:
这是一个单位阵,作用在任何一个向量\([a,b]\)上,仍然会得到\([a,b]\)。
本质原因是:
-
单位阵第一行\([1,0]\),代表的是基向量\(\boldsymbol i = [1,0]\)变换后的位置;
-
同理,单位阵第二行\([0,1]\),代表的是基向量\(\boldsymbol j = [0,1]\)变换后的位置。
显然两个基向量的位置都没发生变化,因此这个变换没有任何变化效果。
而\(a\)是基向量\(\boldsymbol i\)是权重,\(b\)是基向量\(\boldsymbol j\)是权重,\([a,b]\)可以拆解为\(a\boldsymbol i + b\boldsymbol j\)。
由线性性,对任意一个向量\([a,b]\)进行线性变换,等于两个分量分别变换,再相加。
因此任意一个向量与单位阵相乘仍然是其本身。
再举一个例子。设有矩阵:
与向量\([a,b]\)相乘,结果为:
如果理解了矩阵和变换的含义,理解这个结果就特别简单:
-
基向量\(\boldsymbol i\)纹丝不动,而基向量\(\boldsymbol j\)变换到了\([\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]\)。
-
\([a,b]\)可以拆解为\(a\boldsymbol i + b\boldsymbol j\);
-
因此\([a,b]\)变换到了\(a[1,0] + b[\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]\),结果就是\([a+\frac{1}{\sqrt{2}}b,\frac{1}{\sqrt{2}}b]\)
4. 一维矩阵也是一种线性变换
线性性对我们的证明特别重要,可以解释为什么能分别对基向量作变换,再叠加。
我们都知道,线性性包含齐次性和叠加性。
要证明某一个变换是线性变换,就必须证明该变换具有这两个性质。
我们在这里省略严格的证明,换一个直观的角度予以证明。
线性变换有一个直观的特点:
在二维空间中,如果有一系列等距分布于同一直线上的点:
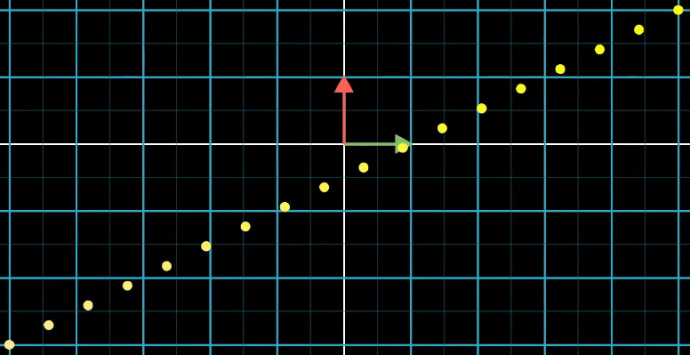
那么线性变换之后,这些点在数轴上仍是等距分布的:

能证明这一点暂时就足够了。
与上一节不同的是,我们现在介绍的是降维变换(2D→1D)。但矩阵和变换的关系还是相同的:
原本二维空间的基向量是[1,0],[0,1]:
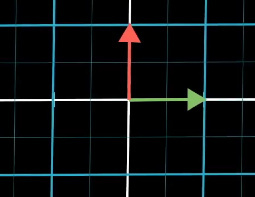
现在变成了数轴上的两个点,也就是两个数(动画更直观,推荐看视频):

该过程满足保持等距条件。
因为如果把作用向量放大\(\alpha\)倍,实际上就是把两个基向量的权重分别放大\(\alpha\)倍。
被变换作用后再叠加,效果也是放大\(\alpha\)倍。因此等距点仍然是等距点。
这样,我们就粗略说明了该变换是线性变换。
因此我们完全可以认为:
向量[2,1]表征一个从二维到一维的线性变换,将基向量\(\boldsymbol i\)变换至数轴点2,将基向量\(\boldsymbol j\)变换至数轴点1。
5. 最终解释:为什么是投影
现在,我们解释为什么点积可以用投影后的乘积来解释。
我们先来看一个单位向量\(\boldsymbol u\)。
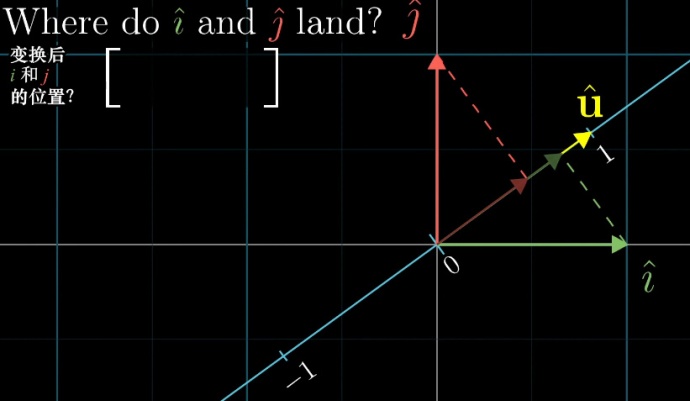
由于是单位向量,因此\(\boldsymbol i = [1,0]\)往\(\boldsymbol u\)上做投影,和\(\boldsymbol u\)往\(\boldsymbol i = [1,0]\)(也即x轴)上做投影,长度是一样的!
也就是说:图中绿色虚线投影得到的投影长度,等于\(\boldsymbol u\)的横坐标\(u_x\)。
同理:图中红色虚线投影得到的投影长度,等于\(\boldsymbol u\)的纵坐标\(u_y\)。

好了。此时假设向量\(\boldsymbol w\)要和单位向量\(\boldsymbol u\)点积。
由上一节推出的性质,基向量在变换\(\boldsymbol u\)下,会分别映射(降维)到点\(u_x\)和\(u_y\)。
设\(\boldsymbol w = [w_x,w_y]\),那么\(\boldsymbol w\)就会映射到\(w_xu_x+w_yu_y\)。
这就是点积!!!
所以,为什么可以理解为:\(\boldsymbol w\)先投影到\(\boldsymbol u\)上,再做乘积呢?
-
\(\boldsymbol w\)可以拆解为基向量的加权组合。
-
每一个基向量与变换\(\boldsymbol u\)(先规定为单位向量)作用的结果,又可以分为:
-
该变换相当于投影到\(\boldsymbol v\)所在数轴上的一点。
-
该点的坐标,正是\(\boldsymbol u\)的横坐标或纵坐标。
-
由线性性,基向量分别变换后再相加,等价于向量\(\boldsymbol w\)整体变换的结果。因此我们把两个投影值相加,就得到了最终结果。
-
-
因此,从计算过程上看就是:坐标和权重相乘,再相加。这就是点积!
-
从投影过程上看:\(\boldsymbol w\)在\(\boldsymbol v\)上投影,恰好也可以拆分成两个基向量在\(\boldsymbol v\)投影的叠加。因此点积都是投影!
-
如果\(\boldsymbol u\)不是单位向量,再乘以其范数即可。这就是完整的点积:投影→相乘!
解释完毕!

