时隔3年,再做双倍超立方数的题目,这次用Lisp
09年的时候,有一阵子大家都在做网易的“有道难题”里面的双倍超立方数问题。我当时看到题目后也随手用 Python 做了一下,但当时那个解法是最笨的穷举法,所以除了练习了一次 Python 的基本语法之外,也没有什么特别的收获了。
最近又把 SICP 翻出来看到了流这一部分。在我发自内心的赞叹那些用流描述的数列在形式上是何等优美的同时,我想实际测量一下应用了这么多复杂的流的函数操作之后,程序的执行效率如何。而双倍超立方数正好是一个适合拿来练习的题目。
这次我用的开发环境是 DrRacket. 这个东西的前身其实叫做 DrScheme. 是 scheme 的一种开发环境,在 Windows 上比较容易安装。而因为 SICP 是用 scheme 语言描述的,所以用这个环境来开发就是理所当然的事了。
双倍超立方数的表述形式为:
c = a^3 + b^3
对给定的c,如果有且只有两组正整数(a, b)使上式成立,那么c就称为双倍超立方数。
基于对称性,可以设 a <= b.
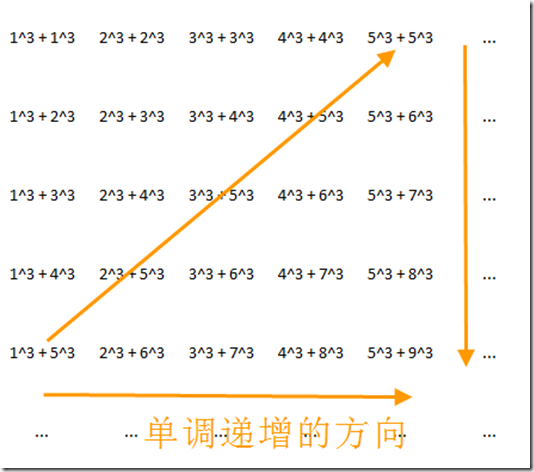
下面我们来观察一下从 1^3 + 1^3 开始的两个自然数的立方和组成的数列是怎样的:
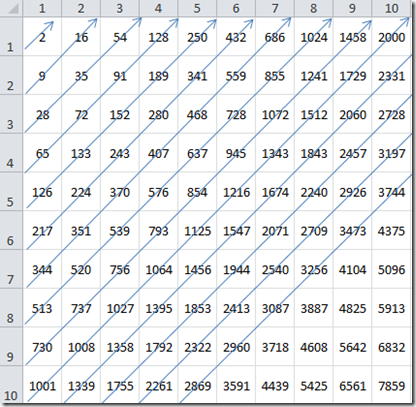
容易观察到,上述图中的 (a, b) 组合是没有重复的。也就是说,这代表了所有 (a, b) 的可能的组合情况。双倍超立方数题目的要求是,比如我们需要求出不超过n(比如100万)的所有双倍超立方数的个数。如果我们能够对上述流中的数字在仅进行一趟从小到大的遍历,在遍历过程中判断出其中哪些立方和出现了2次,则可以有效的减少遍历的次数,得到答案。因此问题的关键转化为如何有效的按立方和从小到大的次序遍历上述矩阵。
可以看到,矩阵中横向、纵向、以及从左下到右上的每一条对角线方向上的数字的立方和都是单调递增的。但是很难直观的对整个矩阵找到这样一条单调递增的遍历路径。
进一步观察计算结果,可以发现,沿对角线方向的数字序列,两两数字之间的间隔最小。可以把每一条对角线上的数字序列定义为一个流,然后所有对角线组成的流进行合并(merge)。合并的方式是,依次取每个流的头部元素互相比较大小,按从小到大的次序组合进结果流中。因为按对角线方向元素间隔相对来说最小,在流进行合并的时候,能够连续的从同一个流中获取多个连续的元素,那么在合并时需要不断切换从不同的流中获取下一个元素的情况应该就比较少一些,如果实现得当,代码的局部性 (locality) 也许会比较好,也许合并算法上也可以有进一步优化的可能。(当然这个只是我目前的推断,还没有证实)
按照这个思路,整个问题解法的步骤如下:
1. 得到一个按大小顺序排列的两个数立方和的流(通过多个对角线的数字流 merge 得到)
在合并的同时,对每个和数出现的次序进行 count. 同时在结果流里面保留每个和出现的次数;
2. 对步骤1得到的流,进行过滤操作 (stream-filter),仅保留上述出现次数恰好为 2 的那些结果;
3. 对步骤2得到的流计算长度 (stream-length),结果就是 <= N 的双倍超立方数的个数。
测试下来发现,N=100万的时候,执行速度还是非常快的,跟 Python 版解法的速度差不多。可以看到,利用流,以及作用于流的各种函数(filter, map, merge 等等操作)作为一种高级的数据结构抽象,可以从另一个角度理解问题。而因为流是惰性求值的,这个特性也使得运算的时间和空间开销等方面都处于一个可接受的范围。
下面是我调试通过的代码。其中还有很大的优化空间,比如很简单的就可以对同一个数字反复求立方的操作进行记忆,避免重复运算的时间开销。
代码的上半部分都是用来操作流的一些通用的帮助函数,有些是 SICP 书里的,另外有几个是我自己写的。双倍超立方数问题的相关实现可以直接看代码的后半部。
执行这个代码可以正确的打印出100万以下双倍超立方数的数目:43.
下面代码中关于流的一些辅助函数的解释,可以参考我上一篇随笔:Racket, SICP stream learning
#lang racket
;***********************************************
; 双倍超立方数问题求解。
;
; 木野狐(Neil Chen)@博客园
;
; 开发环境:DrRacket v5.2.1
; 2012-05-15
;***********************************************
;=========== 准备工作(流操作相关函数)开始 =====
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
(define-syntax cons-stream
(syntax-rules ()
[(cons-stream x y) (cons x (delay y))]))
(define the-empty-stream '())
(define (stream-null? stream)
(null? stream))
(define (stream-filter pred stream)
(cond ((stream-null? stream) the-empty-stream)
((pred (stream-car stream))
(cons-stream (stream-car stream)
(stream-filter pred (stream-cdr stream))))
(else (stream-filter pred (stream-cdr stream)))))
(define (stream-ref s n)
(if (stream-null? s) the-empty-stream
(if (= n 0)
(stream-car s)
(stream-ref (stream-cdr s) (- n 1)))))
(define (stream-map proc . argstreams)
(if (stream-null? (car argstreams))
the-empty-stream
(cons-stream (apply proc (map stream-car argstreams))
(apply stream-map
(cons proc (map stream-cdr argstreams))))))
(define (stream-enumerate-interval low high)
(if (> low high)
the-empty-stream
(cons-stream low
(stream-enumerate-interval (+ low 1) high))))
(define (enumerate-interval low high)
(if (> low high)
'()
(cons low
(enumerate-interval (+ low 1) high))))
(define (stream-length stream)
(define (iter s acc)
(if (stream-null? s) acc
(iter (stream-cdr s) (+ 1 acc))))
(iter stream 0))
;=========== 准备工作(流操作相关函数)结束 ======
(define (integers-starting-from n)
(cons-stream n (integers-starting-from (+ n 1))))
(define integers
(integers-starting-from 1))
(define (cube n)
(* n n n))
(define cube-numbers
(stream-map cube integers))
(define (merge-with-count s1 s2)
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else
(let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(let ((e1 (if (list? s1car) (car s1car) s1car))
(c1 (if (list? s1car) (cadr s1car) 1))
(e2 (if (list? s2car) (car s2car) s2car))
(c2 (if (list? s2car) (cadr s2car) 1)))
(cond ((< e1 e2) (cons-stream (list e1 c1)
(merge-with-count (stream-cdr s1) s2)))
((> e1 e2) (cons-stream (list e2 c2)
(merge-with-count s1 (stream-cdr s2))))
(else (cons-stream (list e1 (+ c1 c2)) (merge-with-count (stream-cdr s1) (stream-cdr s2))))))))))
(define (stream-merge-with-count . argstreams)
(if (= 0 (length argstreams))
the-empty-stream
(merge-with-count (car argstreams)
(apply stream-merge-with-count (cdr argstreams)))))
; 得到第 n 条对角线上的数字的流
(define (diag n)
(stream-map (lambda (i)
(+ (cube i)
(cube n)))
(stream-enumerate-interval 1 n)))
(define (new-double-cubic-numbers-below n)
(let ((max (floor (expt (- n 1) (/ 1 3)))))
(stream-map car
(stream-filter
(lambda (s)
(and (list? s)
(= 2 (cadr s))
(not (> (car s) n))))
(apply stream-merge-with-count
(map diag
(enumerate-interval 1 max)))))))
(stream-length (new-double-cubic-numbers-below 1000000))