先贴一段维基百科的内容:
计算机时代计算π
上万位以上的小数位值通常利用高斯-勒让德算法或波温算法;另外以往亦曾使用于1976年发现的萨拉明-布伦特算法。
第一个π和1/π的小数点后首一百万位利用了古腾堡计划。最新纪录是2002年9月得出的1,241,100,000,000个小数位,由拥有1TB主内存的64-node日立超级计算机,以每秒200亿运算速度得出,比旧纪录多算出一倍(206亿小数位)。此纪录由以下梅钦类公式得出:
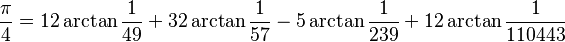 (K. Takano, 1982年)
(K. Takano, 1982年)
 (F. C. W. Störmer, 1896年)
(F. C. W. Störmer, 1896年)
这么多的小数位没什么实用价值,只用以测试超级计算机。
1996年,David H. Bailey、Peter Borwein及西蒙·普劳夫发现了π的其中一个无穷级数:
以上述公式可以计算π的第n个二进制或十六进制小数,而不需先计算首n-1个小数位。此类π算法称为贝利-波尔温-普劳夫公式。请参考Bailey's website 上相关程式。
法布里斯·贝拉于1997年给出了计算机效率上高出上式47%的BBP算法:
请参考Fabrice Bellard's PI page 。
其他计算圆周率的公式包括:
 (拉马努金Ramanujan)
(拉马努金Ramanujan)
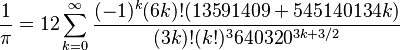 (David Chudnovsky及Gregory Chudnovsky)
(David Chudnovsky及Gregory Chudnovsky)
编写计算机程序时,也可以利用反三角函数直接定义 值,但是编译器必须具备三角函数的函式库:
值,但是编译器必须具备三角函数的函式库:
利用正弦函数
利用余弦函数
几何
- 若圆的半径为r,则其周长为C = 2πr
- 若圆的半径为r,则其面积为S =πr2
- 若椭圆的长、短两轴分别为a 和 b ,则其面积为S = πab
- 若球体的半径为 r,则其体积为 V = (4/3)πr3
- 若球体的半径为r,则其表面积为 S = 4πr2
- 角:180度相等于π弧度
环面的体积和表面积公式
R是管子的中心到画面的中心的距离, r是圆管的半径。
[编辑]代数
π是个无理数,即不可表达成两个整数之比,是由Johann Heinrich Lambert于1761年证明的。 1882年,Ferdinand Lindemann更证明了π是超越数,即不可能是任何有理数多项式的根。
圆周率的超越性否定了化圆为方这古老尺规作图问题的可能性,因所有尺规作图只能得出代数数,而超越数不是代数数。
[编辑]数学分析
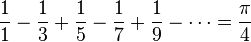 (Leibniz定理)
(Leibniz定理)
 (Wallis乘积)
(Wallis乘积)
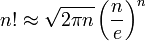 (斯特林公式)
(斯特林公式)
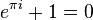 (欧拉公式)
(欧拉公式)
π有个特别的连分数表示式:
π本身的连分数表示式(简写)为[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,...],其近似部分给出的首三个渐近分数
第一个和第三个渐近分数即为约率和密率的值。数学上可以证明,这样得到的渐近分数,在分子或分母小于下一个渐进分数的分数中,其值是最接近精确值的近似值。
(另有12个表达式见于[3] )
[编辑]数论
[编辑]概率论
- 取一枚长度为l的针,再取一张白纸在上面画上一些距离为2l的平行线。把针从一定高度释放,让其自由落体到纸面上。针与平行线相交的概率是圆周率的倒数(泊松针)。曾经有人以此方法来寻找π的值。
[编辑]动态系统/遍历理论
- 对[0, 1]中几乎所有x0,其中 xi是对于r=4的逻辑图像迭代数列。
[编辑]物理学
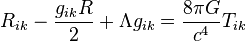 (相对论的场方程)
(相对论的场方程)
[编辑]统计学
求圆周率π的C程序分析
long a=10000, b, c=2800, d, e, f[2801], g;
main(){ for(;b-c;) f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)
for(b=c; d+=f[b]*a, f[b]=d%--g, d/=g--, --b; d*=b); scanf("%s");}
简短的4行代码,就可以精确计算机出800位的PI(圆周率)值。
实在太震撼人心了。这样的程序也能运行,竟然还能能完成这样让人难以置信的任务,真是太神了。
一、源程序
本文分析下面这个很流行的计算PI的小程序。下面这个程序初看起来似乎摸不到头脑,不过不用担心,当你读完本文的时候就能够基本读懂它了。程序一:很牛的计算Pi的程序
#include <stdio.h>
int a=10000,b,c=2800,d,e,f[2801],g;
main()
{
for(;b-c;)
f[b++]=a/5;
for(;d=0,g=c*2;c -=14,printf("%.4d",e+d/a),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b; d*=b);
}
二、数学公式
数学家们研究了数不清的方法来计算PI,这个程序所用的公式如下:
pi = 2 + 1/3 * (2 + 2/5 * (2 + 3/7 * (2 + ... (2 + k/2k+1 * (2 + ... ))...)))
至于这个公式为什么能够计算出PI,已经超出了本文的能力范围。
下面要做的事情就是要分析清楚程序是如何实现这个公式的。
我们先来验证一下这个公式:
程序二:Pi公式验证程序
#include <stdio.h>
void main()
{
float pi=2;
int i;
for(i=100;i>=1;i--)
pi=pi*(float)i/(2*i+1)+2;
printf("%f\n",pi);
getchar();
}
上面这个程序的结果是3.141593。
三、程序展开
在正式分析程序之前,我们需要对程序一进行一下展开。我们可以看出程序一都是使用for循环来完成计算的,这样做虽然可以使得程序短小,但是却很难读懂。根据for循环的运行顺序,我们可以把它展开为如下while循环的程序:
程序三:for转换为while之后的程序
#include <stdio.h>
int a=10000,b,c=2800,d,e,f[2801],g;
main() {
int i;
for(i=0;i<c;i++)
f[i]=a/5;
while(c!=0)
{
d=0;
g=c*2;
b=c;
while(1)
{
d=d+f[b]*a;
g--;
f[b]=d%g;
d=d/g;
g--;
b--;
if(b==0) break;
d=d*b;
}
c=c-14;
printf("%.4d",e+d/a);
e=d%a;
}
}
注:
for([1];[2];[3]) {[4];}的运行顺序是[1],[2],[4],[3]。如果有逗号操作符,例如:d=0,g=c*2,则先运行d=0,然后运行g=c*2,并且最终的结果是最后一个表达式的值,也就是这里的c*2。
下面我们就针对展开后的程序来分析。
四、程序分析
要想计算出无限精度的PI,我们需要上述的迭代公式运行无数次,并且其中每个分数也是完全精确的,这在计算机中自然是无法实现的。那么基本实现思想就是迭代足够多次,并且每个分数也足够精确,这样就能够计算出PI的前n位来。上面这个程序计算800位,迭代公式一共迭代2800次。
int a=10000,b,c=2800,d,e,f[2801],g;
这句话中的2800就是迭代次数。
由于float或者double的精度远远不够,因此程序中使用整数类型(实际是长整型),分段运算(每次计算4位)。我们可以看到输出语句printf("%.4d",e+d/a); 其中%.4就是把计算出来的4位输出,我们看到c每次减少14( c=c-14;),而c的初始大小为2800,因此一共就分了200段运算,并且每次输出4位,所以一共输出了800位。
由于使用整型数运算,因此有必要乘上一个系数,在这个程序中系数为1000,也就是说,公式如下:
1000*pi = 2K+ 1/3 * (2K+ 2/5 * (2K+ 3/7 * (2K+ ... (2K+ k/2k+1 * (2K+ ... ))...)))
这里的2K表示2000,也就是f[2801]数组初始化以后的数据,a=10000,a/5=2000,所以下面的程序把f中的每个元素都赋值为2000:
for(i=0;i<c;i++)
f[i]=a/5;
你可能会觉得奇怪,为什么这里要把一个常数储存到数组中去,请继续往下看。
我们先来跟踪一下程序的运行:
while(c!=0) //假设这是第一次运行,c=2800,为迭代次数
{
d=0;
g=c*2; //这里的g是用来做k/(2k+1)中的分子
b=c; //这里的b是用来做k/(2k+1)中的分子
while(1)
while(1)
{
d=d+f[b]*a; //f中的所有的值都为2000,这里在计算时又把系数扩大了a=10000倍。这样做的目的稍候介绍,你可以看到输出的时候是d/a,所以这不影响计算
g--;
f[b]=d%g; //先不管这一行
d=d/g; //第一次运行的g为2*2799+1,你可以看到g做了分母
g--;
b--;
if(b==0) break;
d=d*b; //这里的b为2799,可以看到b做了分子。
}
c=c-14;
printf("%.4d",e+d/a);
e=d%a;
}
只需要粗略的看看上面的程序,我们就大概知道它的确是使用的那个迭代公式来计算Pi的了,不过不知道到现在为止你是否明白了f数组的用处。如果没有明白,请继续阅读。
d=d/g,这一行的目的是除以2k+1,我们知道之所以程序无法精确计算的原因就是这个除法。即使用浮点数,答案也是不够精确的,因此直接用来计算800位的Pi是不可能的。那么不精确的成分在哪里?很明显:就是那个余数d%g。程序用f数组把这个误差储存起来,在下次计算的时候使用。现在你也应该知道为什么d=d+f[b]*a;中间需要乘上a了吧。把分子扩大之后,才好把误差精确的算出来。
d如果不乘10000这个系数,则其值为2000,那么运行d=d/g;则是2000/(2*2799+1),这种整数的除法答案为0,根本无法迭代下去了。
现在我们知道程序就是把余数储存起来,作为下次迭代的时候的参数,那么为什么这么做就可以使得下次迭代出来的结果为接下来的数字呢?
这实际上和我们在纸上作除法很类似:
0142
/———
7/ 1
10
7
——————
30
28
——————
20
14
——————
6
.....
我们可以发现,在做除法的时候,我们通常把余数扩大之后再来计算,f中既然储存的是余数,而f[b]*a;则正好把这个余数扩大了a倍,然后如此循环下去,可以计算到任意精度。
这里要说明的是,事实上每次计算出来的d并不一定只有4位数,例如第一次计算的时候,d的值为31415926,输出4位时候,把低四位的值储存在e中间,e=d%a,也就是5926。
最后,这个c=c-14不太好理解。事实上没有这条语句,程序计算出来的仍然正确。只是因为如果迭代2800次,无论分数如何精确,最后Pi的精度只能够达到800。
你可以把程序改为如下形式尝试一下:
for(i=0;i<800;i++)
{
{
d=0;
g=c*2;
b=c;
while(1)
{
d=d+f[b]*a;
g--;
f[b]=d%g;
d=d/g;
g--;
b--;
if(b==0) break;
d=d*b;
}
//c=c-14; //不要这句话。
printf("%.4d",e+d/a);
e=d%a;
}
最后的答案仍然正确。
不过我们可以看到内循环的次数是c次,也就是说每次迭代计算c次。而每次计算后续位数的时候,迭代次数减少14,而不影响精度。
还有一篇相关文章:转自http://www.yangfei.org/post/74.html
网上流传着一个怪异的求pi程序,虽然只有三行却能求出pi值连小数点前共800位。你可以运行一下试试,我第一次运行也被这程序吓住了。这个程序如下:
/*某年Obfuscated C Contest佳作选录:*/
#include < stdio.h>
long a=10000, b, c=2800, d, e, f[2801], g;
main(){
for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
}
/* (本程式可算出pi值连小数点前共800位)
(本程式录自sci.math FAQ,原作者未详)*/
咋一看,这程序还挺吓人的。别慌,下面就告诉你它是如何做到的,并且告诉你写怪异C程序的一些技巧。^_^
展开化简
我们知道,在C语言中,for循环和while循环可以互相代替。
for(statement1;statement2;statement3){
statements;
}
上面的for语句可以用下面的while语句来代替:
statement1;
while(statement2){
statements;
statement3;
}
而且要写怪异的C程序,逗号运算符无疑是一个好的助手,它的作用是:
从左到右依次计算各个表达式的值,并且返回最右边表达式的值。
把它嵌入for循环中是写怪异代码的常用技巧之一。所以,上面的程序可以展开为:
#include < stdio.h> /*1*/
/*2*/
long a=10000, b, c=2800, d, e, f[2801], g; /*3*/
main(){ /*4*/
while(b-c!=0){ /*5*/
f[b]=a/5; /*6*/
b++; /*7*/
} /*8*/
d=0; /*9*/
g=c*2; /*10*/
while(g!=0){ /*11*/
b=c; /*12*/
d+=f[b]*a; /*13*/
f[b]=d%--g; /*14*/
d=d/g--; /*15*/
--b; /*16*/
while(b!=0){ /*17*/
d=d*b+f[b]*a; /*18*/
f[b]=d%--g; /*19*/
d=d/g--; /*20*/
--b; /*21*/
} /*22*/
c-=14; /*23*/
printf("%.4d",e+d/a); /*24*/
e=d%a; /*25*/
d=0; /*26*/
g=c*2; /*27*/
} /*28*/
} /*29*/
现在是不是好看一点了?
进一步化简
你应该能注意到a的值始终是10000,所以我们可以把a都换成10000。再就是,仔细观察g,在外层循环中,每次循环用它做除法或取余时,它总是等于2*c-1,而b总是初始化为c。在内层循环中,b每次减少1,g每次减少2。你这时会想到了吧?用2*b-1代替g!代进去试试,没错!另外,我们还能做一点化简,第26行的d=0是多余的,我们把它合并到第13行中去,第13行可改写为: d=f[b]*a; 。所以程序可以改为:
#include < stdio.h>
long b, c=2800, d, e, f[2801];
main(){
while(b-c!=0){
f[b]=2000;
b++;
}
while(c!=0){
b=c;
d=f[b]*10000;
f[b]=d%(b*2-1);
d=d/(b*2-1);
--b;
while(b!=0){
d=d*b+f[b]*10000;
f[b]=d%(b*2-1);
d=d/(b*2-1);
--b;
}
c-=14;
printf("%.4d",e+d/10000);
e=d%10000;
}
}
少了两个变量了!
深入分析
好了,马上进入实质性的分析了。一定的数学知识是非常有必要的。首先,必须知道下面的公式可以用来求pi:
pi/2=1+1!/3!!+2!/5!!+3!/7!!+...+k!/(2*k+1)!!+...(注:双阶乘
双阶乘m!!表示: 当m是自然数时,表示不超过m且与m有相同奇偶性的所有正整数的乘积。如:3!!=1*3=3,6!!=2*4*6=48(另0!!=1) 当m是负奇数时,表示绝对值小于它的绝对值的所有负奇数的绝对值积的倒数。如:(-7)!!=1/(|-5| * |-3| * |-1|)=1/15 当m是负偶数时,m!!。
(2n-1)!!=1*3*5*7......(2n-1)
(2n)!!=2*4*6*8...........(2n)
比如7!!=1*3*5*7
8!!=2*4*6*8)
只要项数足够多,pi就有足够的精度。至于为什么,我们留给数学家们来解决。
写过高精度除法程序的人都知道如何用整数数组来进行除法用法,而避免小数。其实很简单,回想一下你是如何徒手做除法的。用除数除以被除数,把得数放入结果中,余数乘以10后继续做下一步除法,直到余数是零或达到了要求的位数。
原程序使用的数学知识就那么多,之所以复杂难懂是因为它把算法非常巧妙地放到循环中去了。我们开始具体来分析程序。首先,我们从数学公式开始下手。我们求的是pi,而公式给出的是pi/2。所以,我们把公式两边同时乘以2得:
pi=2*1+2*1!/3!!+2*2!/5!!+2*3!/7!!+...+2*k!/(2*k+1)!!+...
接着,我们把它改写成另一种形式,并展开:
pi=2*1+2*1!/3!!+2*2!/5!!+2*3!/7!!+...+2*n!/(2*n+1)!!
=2*(n-1)/(2*n-1)*(n-2)/(2*n-3)*(n-3)/(2*n-5)*...*3/7*2/5*1/3
+2*(n-2)/(2*n-3)*(n-3)/(2*n-5)*...*3/7*2/5*1/3
+2*(n-3)/(2*n-5)*...*3/7*2/5*1/3
+2*3/7*2/5*1/3
+2*2/5*1/3
+2*1/3
+2*1
对着公式看看程序,可以看出,b对应公式中的n,2*b-1对应2*n-1。b是从2800开始的,也就是说n=2800。(至于为什么n=2800时,能保证pi的前800位准确不在此讨论范围。)看程序中的相应部分:
d=d*b+f[b]*10000;
f[b]=d%(b*2-1);
d=d/(b*2-1);
d用来存放除法结果的整数部分,它是累加的,所以最后的d将是我们要的整数部分。而f[b]用来存放计算到b为止的余数部分。
到这里你可能还不明白。一是,为什么数组有2801个元素?很简单,因为作者想利用f[1]~f[2800],而C语言的数组下标又是从0开始的,f[0]是用不到的。二是,为什么要把数组元素除了f[2800]都初始化为2000?10000有什么作用?这倒很有意思。因为从printf("%.4d",e+d/10000); 看出d/10000是取d的第4位以前的数字,而e=d%10000; ,e是d的后4位数字。而且,e和d差着一次循环。所以打印的结果恰好就是我们想要的pi的相应的某4位!开始时之所以把数组元素初始化为2000,是因为把pi放大1000倍才能保证整数部分有4位,而那个2就是我们公式中两边乘的2!所以是2000!注意,余数也要相应乘以10000而不是10!f[2800]之所以要为0是因为第一次乘的是n-1也就是2799而不是2800!每计算出4位,c都要相应减去 14,也就保证了一共能够打印出4*2800/14=800位。但是,这竟然不会影响结果的准确度!本人数学功底不高,无法给出确切答案。(要是哪位达人知道,请发email到xiyou.wangcong@gmail.com告诉我哦。)
偶然在网上见到一个根据上面的程序改写的“准确”(这个准确是指没有漏掉f[]数组中的的任何一个元素。)打印2800位的程序,如下:
long b,c=2800,d,e,f[2801],g;
int main(int argc,char* argv[])
{
for(b=0;b f[b] = 2;
e=0;
while(c > 0)
{
d=0;
for(b=c;b>0;b--)
{
d*=b;
d+=f[b]*10;
f[b]=d%(b*2-1);
d/=(b*2-1);
}
c-=1;
printf("%d",(e+d/10)%10);
e=d%10;
}
return 0;
}
不妨试试把上面的程序压缩成3行。
我稀里糊涂算是看完了,但是对那个计算π的公式还是没有推出来。我翻了一下高数课本,找了一下arcsin和 arccos的幂级数公式
arccos的幂级数公式
arccosx
=π/2-arcsinx
=π/2-∫[0,x]d(arcsinx)
=π/2-∫[0,x]dx/√(1-x^2)
=π/2-∫[0,x]∑[(2k)!/(2^k*k!)^2]x^(2k)
=π/2-∑[(2k)!/((2k+1)(2^k*k!))]x^(2k+1)(k=0,1,2,3,4.....),
如果让x=1,可以得到arccos1 = 0 =
=π/2-∑[(2k)!/((2k+1)(2^k*k!))]x^(2k+1)(k=0,1,2,3,4.....),
所以
π/2 = ∑[(2k)!/((2k+1)(2^k*k!))]x^(2k+1)(k=0,1,2,3,4.....),
但是和给的公式不一样,不知道那个是怎么推出来的。


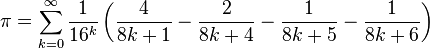
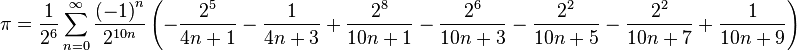
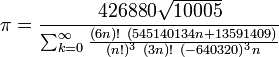

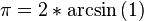





 (由
(由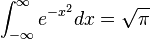
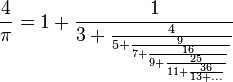

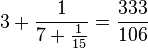

 。
。 个方法写成两个
个方法写成两个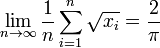
 (
( (此为
(此为