读贾志鹏线性筛有感 (莫比乌斯函数的应用)
先拜大牛。感谢贾志鹏严谨的思维。以及简单清晰的论文描述。
一定要结合论文看。我只是提出我觉得关键的部分。论文在网上随处可见。贾志鹏线性筛。
开头两种线性筛的比较。
一种是传统的线性筛。时间复杂度为N*log(log(N))。
另外一种是优化了合数的筛法。文中称作Euler线性筛。
其优化的地方。
举个例子：合数6。 是2的倍数也是3的倍数。 当你用传统的筛法的时候在遍历2的倍数的时候会遍历到6。遍历3的倍数的时候同样也会遍历到6。
而另外一种只会筛出6为2的倍数。3就不会筛6了。
另外个人认为筛法二有一个很重要的思想。当i为合数的时候。其实脑海里不认为是合数。而是素数的乘积。这样就能比较直观地确定这个算法的正确性了。
积性函数。
分为完全积性和条件积性。
我们最喜欢的积性。大概就是互素积性了。因为满足互素积性的话。根据算术基本定理。就能够简单做到推广到任意实数。
f(1) = 1 。 这个在我们高中数学题。抽象函数。就已经能简单知道了。
欧拉函数。就不再谈了。包括其线性筛的那一步至关重要的证明。也在我其它博文提到过了。
其 欧拉定理和费马小定理的作用。我得再多补充一点。
以及互质数和。 n的互质数和为 n*φ(n)/2.
莫比乌斯函数和容斥定理的关系。
可以发现莫比乌斯函数其实就是容斥定理的映射一般。
莫比乌斯函数 是我们再熟悉不过的了。不熟悉可以看这里。
首先看 (-1)^r m = p1p2p3p4p5pr 其实就是在模拟容斥定理。
假如一但不是素数。那就为0.
两个函数的线性筛。这其实是我们处理问题的基本。这里需要讲的是。不一定只有积性函数才可以用这种筛法。
只要你能找到f(kn) n整除k 和不整除的两个时刻所对应的递推式。这个在扩展问题中会出现。
问题一：求1~N对质数P的乘法逆元。
关于f(n)为完全积性函数。根据同余定理可以简单获得。要证明的话。减法证同余即可。
P = nt + k
n' ≡ n*(t^2)*f(k)^2 (mod P)
这个证明过程很漂亮(很佩服这么顺畅,思维这么清晰)。也是根据同余定理。还有逆元的性质。就能推理的。
这个问题的意义。可以求N!的 mod P 的逆元了。逆元还是很有用的。因为毕竟除法并没有特别好的同余式。（依稀还记得那两个。）
问题二：给T组N,M.依次求出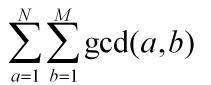
的值.(N,M<=10^6,T<=10^3)
求解gcd(a,b).把gcd(a,b)当做n.再通过欧拉函数和式。推导过程如下。
第二个等式是用d来看待式子的方法来化简和式的。
之后再穷举d即可。
#include<stdio.h> #include<string.h> #define N 100 bool mark[N+5]; int prime[N+5]; int num; int euler[N+5]; int Min(int a,int b){return a>b?a:b;} void Euler() { int i,j; num = 0; memset(euler,0,sizeof(euler)); memset(prime,0,sizeof(prime)); memset(mark,0,sizeof(mark)); euler[1] = 1; // multiply function for(i=2;i<=N;i++) { if(!mark[i]) { prime[num++] = i; euler[i] = i-1; } for(j=0;j<num;j++) { if(i*prime[j]>N){break;} mark[i*prime[j]] = 1; if(i%prime[j]==0) { euler[i*prime[j]] = euler[i]*prime[j]; break; } else { euler[i*prime[j]] = euler[prime[j]]*euler[i]; } } } } int main() { int i; int M1,M2; Euler(); for(i=0;i<num;i++)printf("%d ",prime[i]); printf("\n"); for(i=1;i<=N;i++)printf("%d ",euler[i]); printf("\n"); M1 = 2; M2 = 3; int sum = 0; int min = Min(M1,M2); for(i=1;i<=min;i++) { sum += euler[i]*(M1/i)*(M2/i); } printf("%d\n",sum); }
问题三：给T组N,M.依次求出
的值.(N,M<=10^6,T<=10^3)
在证明之前，先证明以下式子。
问题的解决推导。
第一个等式。lcm(a,b) = ab/gcd(a,b).
第二个等式。令d=gcd(a,b)。
第三个等式。转化为d的视角。（这个手法经常有）。
第四个等式。转化为莫比乌斯函数。
第五个等式。利用上述的等式来转化。注意d和d'
第六个等式。论文中提到的有趣的化简性质。
第七个等式。其实是d = dd'换元。不过有点老奸巨猾啊。干嘛不设个T = dd'。这个我纠结了半天。
之后就是如论文中介绍的。g(d) 为积性函数。线性筛之。
总体上算法还是N的。
问题四：给T组N,M.依次求出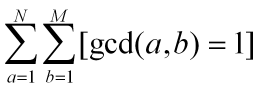
的值.(N,M<=10^6,T<=10^3)
实质上就是求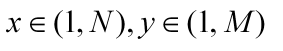 
其中x和y互素。的对数。
我们是时候需要有和式化成的思想了。[gcd(a,b)=1]真是漂亮的莫比乌斯函数的和式的结果。
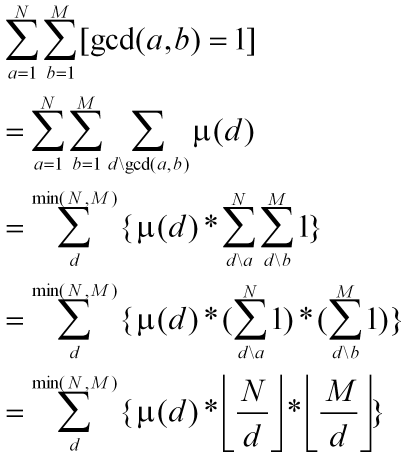
第一个等式：莫比乌斯函数扩写
第二个等式：gcd(a,b)=p -> gcd(a/p,b/p)=1问题转换。
第三个等式：一个和式的处理手段。
第四个等式：很常见的。
#include<stdio.h> #include<string.h> #define N 100 bool mark[N+5]; int prime[N+5]; int num; int mobi[N+5]; int Min(int a,int b){return a>b?a:b;} void Mobi() { int i,j; num = 0; memset(mobi,0,sizeof(mobi)); memset(prime,0,sizeof(prime)); memset(mark,0,sizeof(mark)); mobi[1] = 1; // multiply function for(i=2;i<=N;i++) { if(!mark[i]) { prime[num++] = i; mobi[i] = -1; } for(j=0;j<num;j++) { if(i*prime[j]>N){break;} mark[i*prime[j]] = 1; if(i%prime[j]==0) { mobi[i*prime[j]] = 0; break; } else { mobi[i*prime[j]] = mobi[prime[j]]*mobi[i]; } } } } int main() { int i; int M1,M2; Mobi(); for(i=0;i<num;i++)printf("%d ",prime[i]); printf("\n"); for(i=1;i<=N;i++)printf("%d ",mobi[i]); printf("\n"); M1 = 2; M2 = 3; int sum = 0; int min = Min(M1,M2); for(i=1;i<=min;i++) { sum += mobi[i]*(M1/i)*(M2/i); } printf("%d\n",sum); }
问题五：给T组N.依次求出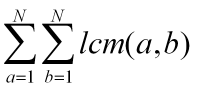
的值.(N<=10^6,T<=10^3)
其实根据问题三.可以直接获得该化简出来的式子的。
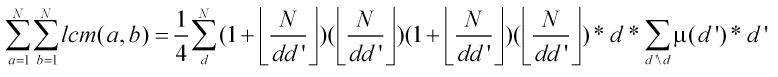
然后解法和问题三一样。
但是论文上寻找积性f(n)直接筛出答案。
首先佩服一下其思维的紧密。一个变量啊。就寻找积性函数。这个转化真是清晰而又巧。
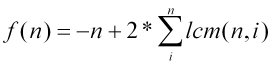
画个图就能知道 -n 是用来去重复的统计的。
.
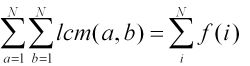f(n)是积性的。具体证明如论文上解释。
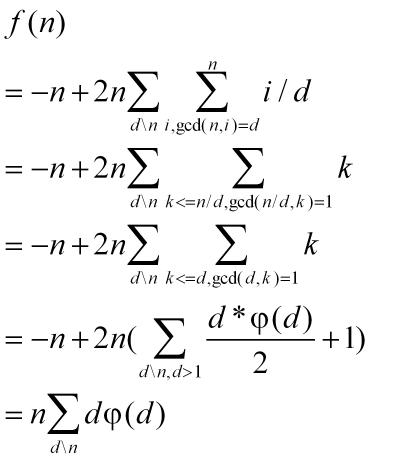
第一个等式:d = gcd(n,i)
第二个等式:k = i/d.且全部都除以d.gcd(a,b)=d转化成求互素(gcd(a,b)=1)的问题。
第三个等式:令d=n/d。是对应的。 其实在第二个等式就能看出是欧拉函数求约数和问题了。
第四个等式:不解释了吧。
第五个等式:手算一下容易得。
欧拉函数求互质数和的函数是积性函数
有一道题。就是利用这个。后会介绍。
见到积性函数我们现在应该是very happy的。
扩展问题1: T组N.依次求出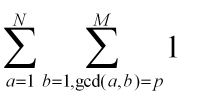
的值.(N<=10^6,T<=10^3)
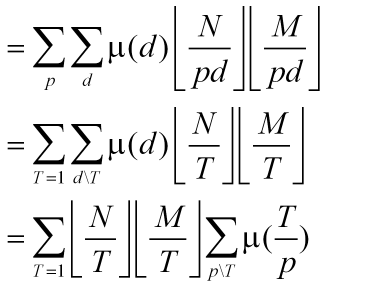
借鉴了贾志鹏上面所有问题的证明。这个是我自己写的扩展证明。难免有错误。见谅。还望留言提醒。
我觉得这样的证明是非常轻快明了的。然后网上还有流行一种。用莫比乌斯反演的另外一种表示式的。也是非常神奇的。
不过。那个反演我还没有证明过。不过还是借鉴了其下半部分的设T。（也是这个设T点醒了我。贾志鹏第3个问题的证明的最后一步。）
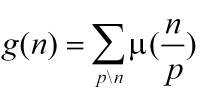这里并不能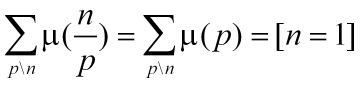
因为p是素数。而n/p不一定是素数。所以并不是对称的。(如果看过具体数学就能很快明白了。)
处理。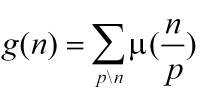
分类对于 g(kx) .有
g(kx)=μ(x) k|p
g(kx)=μ(x)-g(x) k!|p
结合莫比乌斯函数。可以知道分类成立:
我们可以借这个 并且借用之前两个积性函数的筛法 来筛 g(n)。
这是明显可行的。也就是说。我们不需要函数必须是积性的才能去筛。
我们只需要找到g(kx)是由g(x)获得的。或者是在g(x)之前就筛掉的值获得的。eg:g(x-1) (筛法总是从小到大。)
更甚的是。我们只需要获得大值和小值的关系！就可以筛法。但是该筛法。是建立在素数表达式之上的。
这段阐述也许很混乱。但是我也只能描述个大概的个人体会。理解不理解没关系。
给你个例子。筛一个数的素因子之和。
对于上述的筛法.
让F[n] 为n的素因子之和。
F[i*prime[j]] = F[i]+prime[j] i\prime[j]时。
F[i*prime[j]] = F[i]+prime[j] i!\prime[j]时。
两种情况是一样的。原因显而易见。不过我们还是得判断。因为i\prime[j]的时候我们更新后可以直接break;
再考虑一个问题:筛一个数的所拥有的素因子之和。 比如12 为2*2*3 我们只计算2+3.
那么有：
F[i*prime[j]] = F[i] i\prime[j]时。
F[i*prime[j]] = F[i]+prime[j] i!\prime[j]时。
对于这个问题的code.
#include<stdio.h> #include<string.h> #define N 100 int num,prime[N+5],f[N+5]; bool mark[N+5]; void Init() { int i,j; num = 0; f[1] = 0; for(i=2;i<=N;i++) { if(!mark[i]) { prime[num++] = i; f[i] = i; } for(j=0;j<num;j++) { if(i*prime[j]>N){break;} mark[i*prime[j]] = 1; if(i%prime[j]==0) { f[i*prime[j]] = f[i]; break; } else { f[i*prime[j]] = f[i]+prime[j]; } } } } int main() { int i; Init(); for(i=1;i<=N;i++) { printf("%d = %d \n",i,f[i]); } }
再考虑一个问题：筛一个数的所拥有的不重复的素因子之和。比如12 为2*2*3 我们只计算3
那么有：
i\prime[j]时。
情况1: （i/prime[j]）\prime[j]时.
F[i*prime[j]] = F[i]
情况2： （i/prime[j]）！\prime[j]时.
FF[i*prime[j]] = F[i]-prime[j].
i!\prime[j]时。
F[i*prime[j]] = F[i]+prime[j]
#include<stdio.h> #include<string.h> #define N 100 int num,prime[N+5],f[N+5]; bool mark[N+5]; int Max(int a,int b) { return a>b?a:b; } void Init() { int i,j; num = 0; f[1] = 0; for(i=2;i<=N;i++) { if(!mark[i]) { prime[num++] = i; f[i] = i; } for(j=0;j<num;j++) { if(i*prime[j]>N){break;} mark[i*prime[j]] = 1; if(i%prime[j]==0) { if((i/prime[j])%prime[j]==0) { f[i*prime[j]] = f[i]; } else { f[i*prime[j]] = f[i] - prime[j]; } break; } else { f[i*prime[j]] = f[i]+prime[j]; } } } } int main() { int i; Init(); for(i=1;i<=N;i++) { printf("%d = %d \n",i,f[i]); } }
扩展问题1: T组N.求1~N范围上与N互素的数的和。
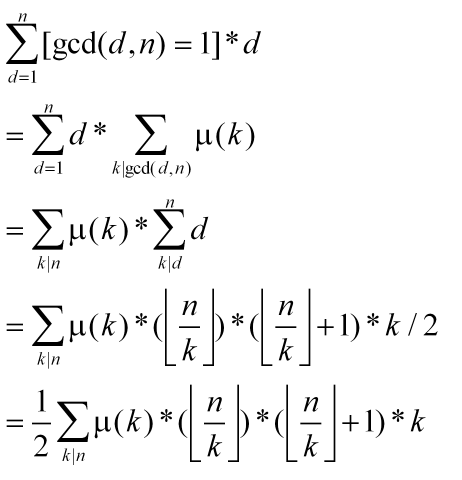
值得一提的是推导到最后的。按照以往的手段似乎没有继续下去的可能了。（但是如果你仔细观察的话。可以发现 n/k 不需要取底符号。那么就能提取出一个n的因子）
Code:
#include<stdio.h> #include<string.h> #define N 100 int num; int prime[N+5]; int mobius[N+5]; bool mark[N+5]; void Mobius() { int i,j; num = 0; mobius[1] = 1; for(i=2;i<=N;i++) { if(!mark[i]) { prime[num++] = i; mobius[i] = -1; } for(j=0;j<num;j++) { if(i*prime[j]>N){break;} mark[i*prime[j]] = 1; if(i%prime[j]==0) { mobius[i*prime[j]] = 0; } else { mobius[i*prime[j]] = -mobius[i]; } } } } int solve(int n) { int i,r; r = 0; for(i=1;i<=n;i++) { if(n%i==0) { r += mobius[i]*i*(n/i)*(n/i+1); } } r /= 2; return r; } int main() { int i,n; Mobius(); while(scanf("%d",&n)!=EOF) { printf("%d = %d\n",n,solve(n)); } }
实际上求互质数和有 n*φ(n)/2 。
用莫比乌斯函数表示
上面公式得证。十分感谢yzq986的留言。告诉了我后续的解法！！！~~~
如果我们直接用n*φ(n)/2。该函数我们是可以直接筛出来的。
对于互质数我们探讨得较多了。个数（欧拉函数）。互素数和。就是以上的。
那么对于约数呢？另外开一篇随笔去探讨这个问题。
论文上的一个优化:
论文上sqrt的优化具体原理论文已经给得很清楚了。
即存在 a/x = a/(x+k) 这个是取整除法
稍微讲述一下代码的构造。
我们预处理出目标函数之后。再预处理出其前缀和用sum数组保存.通过以下代码进行结果的处理。即可。
for(int i=1,last;i<=n;i=last+1) { last = min(n/(n/i),m/(m/i)); ans += (n/i)*(m/i)*(sum[last]-sum[i-1]); }
欢迎点个赞~
