[数学][转载][柏林噪声]
原文:http://freespace.virgin.net/hugo.elias/models/m_perlin.htm
转自:http://www.azure.com.cn/article.asp?id=291
柏林噪声(Perlin Noise)(译)
原文链接:http://freespace.virgin.net/hugo.elias/models/m_perlin.htm
翻译:azure
Many people have used random number generators in their programs to create unpredictability, make the motion and behavior of objects appear more natural, or generate textures. Random number generators certainly have their uses, but at times their output can be too harsh to appear natural. This article will present a function which has a very wide range of uses, more than I can think of, but basically anywhere where you need something to look natural in origin. What's more it's output can easily be tailored to suit your needs.
很多人在他们的程序中使用随机数生成器去创造不可预测,使物体的行为和运动表现的更加自然,或者生成纹理。随机数生成器当然是有他们的用途的,但是它们似乎过于苛刻。这篇文章将会展示一个用途十分广泛的功能,甚至其用途比我想到的还要广泛,其结果可以轻易的适合你的需求。
If you look at many things in nature, you will notice that they are fractal. They have various levels of detail. A common example is the outline of a mountain range. It contains large variations in height (the mountains), medium variations (hills), small variations (boulders), tiny variations (stones) . . . you could go on. Look at almost anything: the distribution of patchy grass on a field, waves in the sea, the movements of an ant, the movement of branches of a tree, patterns in marble, winds. All these phenomena exhibit the same pattern of large and small variations. The Perlin Noise function recreates this by simply adding up noisy functions at a range of different scales.
如果你观察自然界中很多事物,你会注意到它们是分形的。它们有着很多层次细节。最平常的例子是山峰轮廓。它包含着高度上的很大变化(山峰),中等变化(丘陵),小的变化(砾石),微小变化(石头)...你可以继续想象。观察几乎所有事物:片状分布于田间草,海中的波浪,蚂蚁的运动方式,树枝的运动,大理石的花纹,风。所有这些现象表现出了同一种的大小的变化形式。柏林噪声函数通过直接添加一定范围内,不同比例的噪声函数来重现这种现象。
To create a Perlin noise function, you will need two things, a Noise Function, and an Interpolation Function.
为了创建一个柏林噪声函数,我们需要两个东西,一个噪声函数和一个插值函数。
Introduction To Noise Functions
噪声函数介绍
A noise function is essentially a seeded random number generator. It takes an integer as a parameter, and returns a random number based on that parameter. If you pass it the same parameter twice, it produces the same number twice. It is very important that it behaves in this way, otherwise the Perlin function will simply produce nonsense.
一个噪声函数基本上是一个种子随机发生器。它需要一个整数作为参数,然后返回根据这个参数返回一个随机数。如果你两次都传同一个参数进来,它就会产生两次相同的数。这条规律非常重要,否则柏林函数只是生成一堆垃圾。
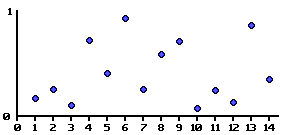
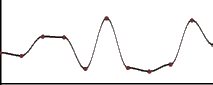
Here is a graph showing an example noise function. A random value between 0 and1 is assigned to every
point on the X axis.
这里的一张图展现了噪声函数的一个例子。X轴上每个点被赋予一个0到1之间的随机数。
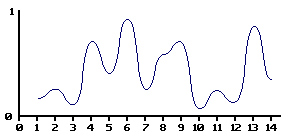
By smoothly interpolating between the values, we can define a continuous function that takes a non-integer as a parameter. I will discuss various ways of interpolating the values later in this article.
通过在值之间平滑的插值,我们定义了一个带有一个非整参数的连续函数。我们将会在后面的内容中讨论多种插值方式。
Definitions
定义
Before I go any further, let me define what I mean by amplitude and frequency. If you have studied physics, you may well have come across the concept of amplitude and frequency applied to a sin wave.
当我们准备深入之前,让我定义下什么是 振幅 (amplitude) 和 频率 (frequency) 。如果你学过物理,你可能遇到过在正弦波中振幅(amlitude)和频率(frequency)的概念。

Sin Wave
The wavelength of a sin wave is the distance from one peak to another. The amplitude is the height of the wave. The frequency is defined to be 1/wavelength.
正弦波
正弦波的波长(wavelength)是两个波峰只间的距离。振幅是此波的高度。频率我们定义为 1/波长(wavelength)。
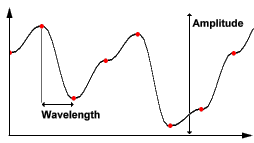
Noise Wave
In the graph of this example noise function, the red spots indicate the random values defined along the dimension of the function. In this case, the amplitude is the difference between the minimum and maximum values the function could have. The wavelength is the distance from one red spot to the next. Again frequency is defined to be 1/wavelength.
噪声波
图中这个噪声波的例子中,红点表示定义沿着在函数维上的随机值。在这种情况下,振幅是这个函数的最大值与最小值的差值。波长(wavelength)是两个红点之间的距离。同样的频率(frequency)定义为1/波长(wavelength)。
Creating the Perlin Noise Function
创建柏林噪声函数
Now, if you take lots of such smooth functions, with various frequencies and amplitudes, you can add them all together to create a nice noisy function. This is the Perlin Noise Function.
现在,如果你使用很多平滑函数,分别拥有各种各样的频率和振幅,你可以把他们叠加在一起来创建一个漂亮的噪声函数。这个就是柏林噪声函数。
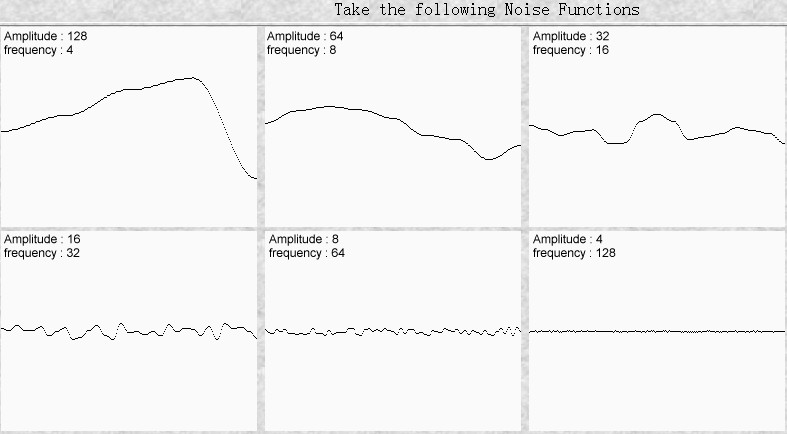
Take the following Noise Functions
使用以下的噪声函数
Add them together, and this is what you get.
将他们叠加起来,你将会得到:-)
You can see that this function has large, medium and small variations. You may even imagine that it looks a little like a mountain range. In fact many computer generated landscapes are made using this method. Of course they use 2D noise, which I shall get onto in a moment.
你能发现这个函数拥有大的,中的和小的变化。你甚至可以它已经有点像山的轮廓了。事实上很多电脑生成地形景观也是使用了这种方法,当然那使用的是2D的噪声,我们将过一下来研究这个。
You can, of course, do the same in 2 dimensions.
你当然同样的可以在二维下也这么做。
Some noise functions are created in 2D
一些2D的噪声函数

Adding all these functions together produces a noisy pattern.
把这些函数叠加起来产生的噪声样式。
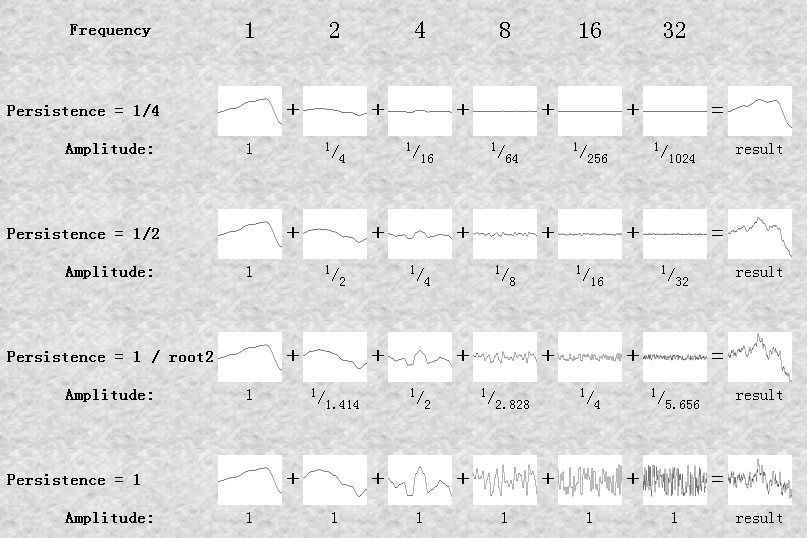
Persistence
持续度
When you're adding together these noise functions, you may wonder exactly what amplitude and frequency to use for each one. The one dimensional example above used twice the frequency and half the amplitude for each successive noise function added. This is quite common. So common in fact, that many people don't even consider using anything else. However, you can create Perlin Noise functions with different characteristics by using other frequencies and amplitudes at each step. For example, to create smooth rolling hills, you could use Perlin noise function with large amplitudes for the low frequencies , and very small amplitudes for the higher frequencies. Or you could make a flat, but very rocky plane choosing low amplitudes for low frequencies.
当你把噪声函数叠加的时候,你可能想了解每次具体使用了什么振幅和频率。上面一维的例子对于每个连续叠加的噪声函数使用 了两倍的频率和二分之一倍的振幅。这个太普通了,事实上太普通,以至于很多人甚至从来都没有考虑过使用其他什么。尽管如此,你可以通过在每步使用其他的频率和振幅来创建不同特征的柏林噪声函数。例如,为了创建一个平滑滚动的丘陵,你可以使用大的振幅和小的频率的柏林噪声函数,同时小的振幅和高的频率,你可以创建一个平地,另外要创建非常颠簸的平面,应该选择小的振幅和低的频率。
To make it simpler, and to avoid repeating the words Amplitude and Frequency all the time, a single number is used to specify the amplitude of each frequency. This value is known as Persistence. There is some ambiguity as to it's exact meaning. The term was originally coined by Mandelbrot, one of the people behind the discovery of fractals. He defined noise with a lot of high frequency as having a low persistence. My friend Matt also came up with the concept of persistence, but defined it the other way round. To be honest, I prefer Matt's definition. Sorry Mandelbrot. So our definition of persistence is this:
为了让这些更简单易懂,同时为了避免重复振幅和频率这两个词,我们用一个数来表示每个频率下的振幅,这个数就是 持续度(Persistence) 。这里的词和它的真实意义有些歧异。这个术语原本是Mandelbrot提出的, 他是发现分形现象的人中的一个。他定义噪声拥有大量的高频率将体现出低的持续度。我的朋友Matt也想出了持续度的概念,但是是通过另外一种方式定义它 的。诚然,我更喜欢Matt的定义方式。对不起了,Mandelbrot. 所以我们这样定义持续度(persistence):
amplitude = persistencei
Where i is the ith noise function being added. To illustrate the effect of persistence on the output of the Perlin Noise, take a look at the diagrams below. They show the component noise functions that are added, the effect of the persistence value, and the resultant Perlin noise function.
i 是表示第i个被叠加的噪声函数。为了展示柏林函数在输出上持续度的表现效果,请看下下面的图表。他们展示了叠加的每个组成部分,持续度的效果和最终的柏林函数。
Octaves
倍频
Each successive noise function you add is known as an octave. The reason for this is that each noise function is twice the frequency of the previous one. In music, octaves also have this property.
每个你所叠加的噪声函数就是一个倍频。因为每一个噪声函数是上一个的两倍频率。在音乐上,倍频也有着这项属性。
Exactly how many octaves you add together is entirely up to you. You may add as many or as few as you want. However, let me give you some suggestions. If you are using the perlin noise function to render an image to the screen, there will come a point when an octave has too high a frequency to be displayable. There simply may not be enough pixels on the screen to reproduce all the little details of a very high frequency noise function. Some implementations of Perlin Noise automatically add up as many noise functions they can until the limits of the screen (or other medium) are reached.
具体多少倍频你叠加在一起,这完全取决于你。你可以叠加很多也可以很少。尽管如此,还是让我给你一些建议吧。如果你正使用柏林噪声函数在屏幕上渲染图象的话,如果倍频频率太高将会使缩成一个点以至于不能显示,这就是因为你屏幕的分辨率不够。一些柏林噪声函数的实现会自动叠加噪声函数直到达到屏幕分辨率的极限。
It is also wise to stop adding noise functions when their amplitude becomes too small to reproduce. Exactly when that happens depends on the level of persistence, the overall amplitude of the Perlin function and the bit resolution of your screen (or whatever).
当振幅变的很小的时候,也应该明智的停止再叠加噪声函数。届时当发生依靠持续度的等级,柏林函数整体的振幅和屏幕的分辨率。
Making your noise functions
创造你的噪声函数
What do we look for in a noise function? Well, it's essentially a random number generator. However, unlike other random number generators you may have come across in your programs which give you a different random number every time you call them, these noise functions supply a random number calculated from one or more parameters. I.e. every time you pass the same number to the noise function, it will respond with the same number. But pass it a different number, and it will return a different number.
我们需要什么样的噪声函数?好,基本上就是一个随机数发生器。尽管如此,它不像你在程序中遇到的那中每次调用它都返回不同的随机数的随机函数,这些噪声函数生成一个随机数是通过一个或者多个参数计算而来。例如,每次你传入一个相同的数到噪声函数里,它将每次也返回相同的随机数。但是如果传入一个不同的数,那么它又将返回一个不同的数。
Well, I don't know a lot about random number generators, so I went looking for some, and here's one I found. It seems to be pretty good. It returns floating point numbers between -1.0 and1.0.
好,我对随机数生成器并不懂太多,所以我去找了一些,这里我找到了一个,好象很好用。它返回一个浮点数,范围是-1.0到1.0
x = (x<<13) ^ x;
return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
end IntNoise function
Now, you'll want several different random number generators, so I suggest making several copies of the above code, but use slightly different numbers. Those big scarey looking numbers are all prime numbers, so you could just use some other prime numbers of a similar size. So, to make it easy for you to find random numbers, I have written a little program to list prime numbers for you. You can give it a start number and an end number, and it will find all the primes between the two. Source code is also included, so you can easily include it into your own programs to produce a random prime number. Primes.zip
现在,你将要需要几个不同的随机数生成器,所以我建议把上面的代码复制几个拷贝,然后稍微修改下里面的参数。那些可怕的数字都是质数,所以你可以改成其他差不多大小的质数(让我想起了 hash key生成),为了让你轻松的找的随机数,我已经写了一个小程序来为你列出质数。你只用输入一个起始值和一个结束值,它找到所有在两值之间的质数。源代码也提供,所以你可以轻松的包含到你自己的程序中来生成随机的质数。
Interpolation
插值
Having created your noise function, you will need to smooth out the values it returns. Again, you can choose any method you like, but some look better than others. A standard interpolation function takes three inputs, a and b, the values to be interpolated between, and x which takes a value between 0 and1. The Interpolation function returns a value between a and b based on the value x. When x equals 0, it returns a, and when x is 1, it returns b. When x is between 0 and1, it returns some value between a and b.
当创建了你的噪声函数,你将需要平滑下他的返回值。再次,你可以选择任何你喜欢的方式, 但是有一些效果更好。一个标准的插值函数需要三个输入,a 和 b, 需要在a和b之间进行插值,还有x,它取值范围是0到1。插值函数返回a到b之间取决与x的一个值。当x等于0,它返回a,当x等于1时,它返回b。当x 是0到1之间时,它将返回a到b之间的某值。
Linear Interpolation:
线性插值
Looks awful, like those cheap 'plasmas' that everyone uses to generate landscapes. It's a simple algorithm though, and I suppose would be excusable if you were trying to do perlin noise in realtime.
看起来很龌龊的,像那些每个人用来生成地形的廉价'plasmas'一样,它是一个简单的算法,如果你想实时的使用柏林噪声函数,这种插值方式是一个选择。

return a*(1-x) + b*x
end of function
Cosine Interpolation:
余弦插值
This method gives a much smother curve than Linear Interpolation. It's clearly better and worth the effort if you can afford the very slight loss in speed.
这个方法线性插值生成了更平滑的曲线。它当然有着更好的效果,如果你愿意稍微损失点速度的话。
ft = x * 3.1415927
f = (1 - cos(ft)) * .5
return a*(1-f) + b*f
end of function
立方插值
This method gives very smooth results indeed, but you pay for it in speed. To be quite honest, I'm not sure if it would give noticeably better results than Cosine Interpolation, but here it is anyway if you want it. It's a little more complicated, so pay attention. Whereas before, the interpolation functions took three inputs, the cubic interpolation takes five. Instead of just a and b, you now need v0, v1, v2 and v3, along with x as before.
这个方法的确是生成了非常平滑的结果,但是你付出的代价就是速度。老实说,我不那么确定它能给你比余弦插值好很多的效果,但是如果你无论如何要使用它的话,它有一点点的复杂,所以这里请注意,之前,插值函数只需要三个参数,但是立方插值需要五个,取代了a和b,现在你需 要v0,v1,v2,v3,x和以前一样也需要。
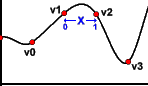
这些是:
v1 = a 点
v2 = b 点
v3 = b 后面一点

P = (v3 - v2) - (v0 - v1)
Q = (v0 - v1) - P
R = v2 - v0
S = v1
return Px3 + Qx2 + Rx + S
end of function
Smoothed Noise
平滑的噪声
Aside from Interplolation, you can also smooth the output of the noise function to make it less random looking, and also less square in the 2D and 3D versions. Smoothing is done much as you would expect, and anyone who has written an image smoothing filter, or fire algorithm should already be familiar with the process.
Rather than simply taking the value of the noise function at a single coordinate, you can take the average of that value, and it's neighbouring values. If this is unclear, take a look at the pseudo code below.
除了插值,你也可以平滑噪声函数的输出来使它看起来不那么随机,和让2D和3D的版本少一点方块。平滑的结果和你所想的差不多,只要是写过平滑过滤或者火焰算法的人都应该相当熟悉此过程。相比在一个单独的坐标上取得噪声值,你可以取平均的噪声值,和它临近的值。如果你不清楚这个,可以看看下面的伪代码。
On the right, you can see a little diagram illustrating the difference between smoothed noise, and the same noise function without smoothing. You can see that the smooth noise is flatter, never reaching the extremes of unsmoothed noise, and the frequency appears to be roughly half. There is little point smoothing 1 dimensional noise, since these are really the only effects. Smoothing becomes more useful in 2 or three dimensions, where the effect is to reduce the squareness of the noise. Unfortunately it also reduces the contrast a little. The smoother you make it, obviously, the flatterthe noise will be.
在右面(这里看下面),你可以看见一个小的图展示了不同平滑函数的区别,和同样的一个噪声但未进行平滑处理。你可以看见平滑函数,从来都没有到底那个未平滑函数的极限值,并且频率显得只有大 约一半。那里有小点平滑一维的噪声,只有这一个效果。平滑过程在二维和三维中,显得更有用处,那就是它减少了噪声大方块。不幸的是它也降低了一点对比度。 你让它越平滑,这个噪声就会越平坦。

1-dimensional Smooth Noise
一维噪声函数
.
.
end function
function SmoothNoise_1D(x)
return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4
end function
二维噪声函数
.
.
end function
function SmoothNoise_2D(x>, y)
corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16
sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8
center = Noise(x, y) / 4
return corners + sides + center
end function
Putting it all together
把它们组合在一起
Now that you know all that, it's time to put together all you've learned and create a Perlin Noise function. Remember that it's just several Interpolated Noise functions added together. So Perlin Noise it just a function. You pass it one or more parameters, and it responds with a number. So, here's a simple 1 dimensional Perlin function.
既然你知道了全部这些,现在是时候把他们组合在一起了,你将学会并创建一个柏林函数。记住这只是几个插值的噪声函数叠加在一起。所以柏林函数只是一个函数。你传入一个或多个参数,然后它返回一个数给你。所以很简单,一维的柏林函数是这样。
The main part of the Perlin function is the loop. Each iteration of the loop adds another octave of twice the frequency. Each iteration calls a different noise function, denoted by Noisei. Now, you needn't actually write lots of noise functions, one for each octave, as the pseudo code seems to suggest. Since all the noise functions are essentially the same, except for the values of those three big prime numbers, you can keep the same code, but simply use a different set of prime numbers for each.
柏林函数重要的部分是那个循环。每次循环跌代叠加另一个两倍频率的倍频。每次跌代调用一个不同的噪声函数,称做Noisei。当然,你并不需要真的写为每个倍频很多噪声函数,伪代码中好象只是建议这么做。既然所有的噪声函数实际上都是相同的,除了那三个大质数不同除外,你可以使用同样的代码,只是每个代码改用不同的质数。
1-dimensional Perlin Noise Pseudo code
一维柏林噪声函数伪代码
x = (x<<13) ^ x;
return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
end function
function SmoothedNoise_1(float x)
return Noise(x)/2 + Noise(x-1)/4 + Noise(x+1)/4
end function
function InterpolatedNoise_1(float x)
integer_X = int(x)
fractional_X = x - integer_X
v1 = SmoothedNoise1(integer_X)
v2 = SmoothedNoise1(integer_X + 1)
return Interpolate(v1 , v2 , fractional_X)
end function
function PerlinNoise_1D(float x)
total = 0
p = persistence
n = Number_Of_Octaves - 1
loop i from 0 to n
frequency = 2i
amplitude = pi
total = total + InterpolatedNoisei(x * frequency) * amplitude
end of i loop
return total
end function
Now it's easy to apply the same code to create a 2 or more dimensional Perlin Noise function:
2-dimensional Perlin Noise Pseudocode
二维柏林噪声函数伪代码
n = x + y * 57
n = (n<<13) ^ n;
return ( 1.0 - ( (n * (n * n * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
end function
function SmoothNoise_1(float x, float y)
corners = ( Noise(x-1, y-1)+Noise(x+1, y-1)+Noise(x-1, y+1)+Noise(x+1, y+1) ) / 16
sides = ( Noise(x-1, y) +Noise(x+1, y) +Noise(x, y-1) +Noise(x, y+1) ) / 8
center = Noise(x, y) / 4
return corners + sides + center
end function
function InterpolatedNoise_1(float x, float y)
integer_X = int(x)
fractional_X = x - integer_X
integer_Y = int(y)
fractional_Y = y - integer_Y
v1 = SmoothedNoise1(integer_X, integer_Y)
v2 = SmoothedNoise1(integer_X + 1, integer_Y)
v3 = SmoothedNoise1(integer_X, integer_Y + 1)
v4 = SmoothedNoise1(integer_X + 1, integer_Y + 1)
i1 = Interpolate(v1 , v2 , fractional_X)
i2 = Interpolate(v3 , v4 , fractional_X)
return Interpolate(i1 , i2 , fractional_Y)
end function
function PerlinNoise_2D(float x, float y)
total = 0
p = persistence
n = Number_Of_Octaves - 1
loop i from 0 to n
frequency = 2i
amplitude = pi
total = total + InterpolatedNoisei(x * frequency, y * frequency) * amplitude
end of i loop
return total
end function





 浙公网安备 33010602011771号
浙公网安备 33010602011771号